
- •§1.1. Понятие ряда Фурье -периодической функции и задача о разложении периодической функции в ряд Фурье
- •Задачи Нарисовать графики и найти ряды Фурье следующих функций, предполагая, что они имеют период :
- •§1.2. Ряд Фурье функции с произвольным периодом
- •§1.3. Разложения только по синусам или только по косинусам
- •§1.4. Лемма Римана - Лебега
- •§1.5. Ядро Дирихле
- •§1.6. Теорема о представимости функции в точке своим рядом Фурье
- •§1.7. Равномерная сходимость рядов Фурье
- •§1.9. Дифференцирование и интегрирование рядов Фурье
- •§1.10. Задача о наилучшем приближении и неравенство Бесселя
- •§1.13. Гладкость функции и скорость сходимости ее ряда Фурье
Задачи Нарисовать графики и найти ряды Фурье следующих функций, предполагая, что они имеют период :
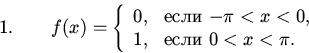
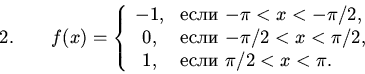
![]()
![]()

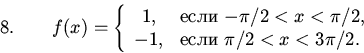
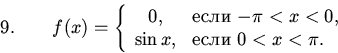
§1.2. Ряд Фурье функции с произвольным периодом
Предположим, что
функция f
задана в промежутке [-l,l],
где l
- некоторое положительное число. Сделав
подстановку
![]() (-у)
получим функцию
(-у)
получим функцию
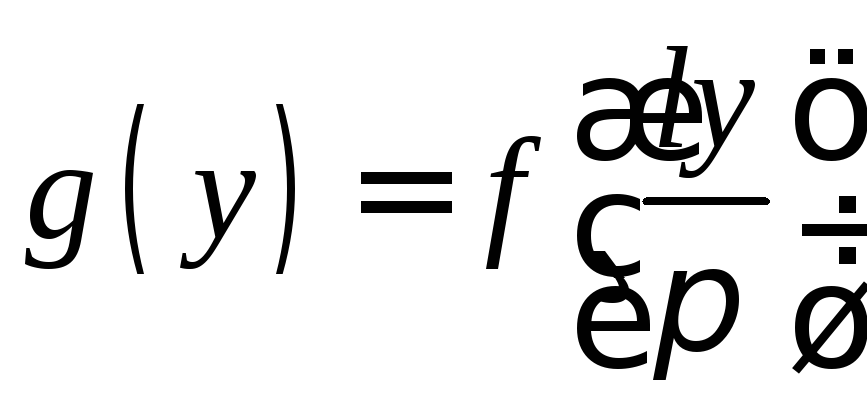 ,
определенную в промежутке [-;].
В соответствии с предыдущим параграфом
функции g
соответствует (формальный) ряд Фурье
,
определенную в промежутке [-;].
В соответствии с предыдущим параграфом
функции g
соответствует (формальный) ряд Фурье
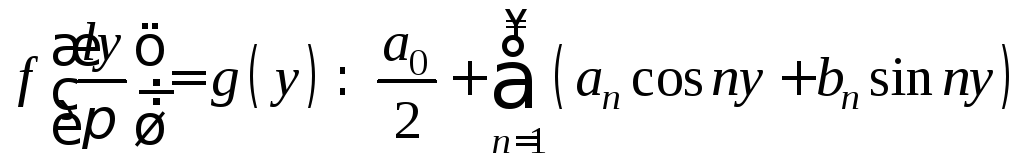 ,
,
коэффициенты которого находятся по формулам Эйлера - Фурье:
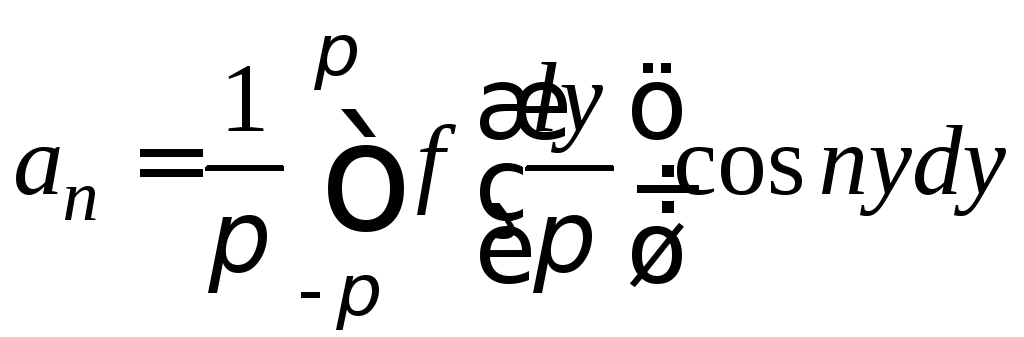 ,
n=0,1,2,…,
,
n=0,1,2,…,
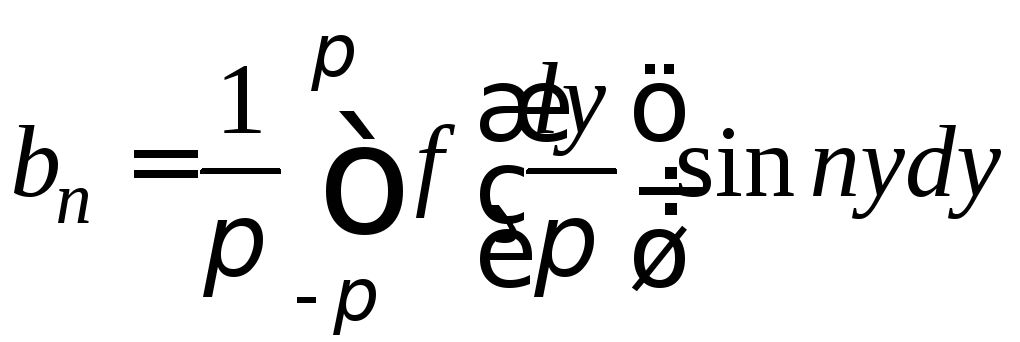 ,
n=1,2,…
,
n=1,2,…
Возвращаясь к
старой переменной, т.е. полагая в
выписанных формулах
![]() ,
мы получим для функцииf
тригонометрический ряд несколько
измененного вида:
,
мы получим для функцииf
тригонометрический ряд несколько
измененного вида:
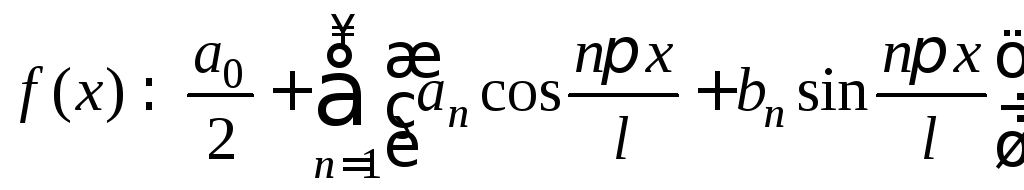 ,
,
где
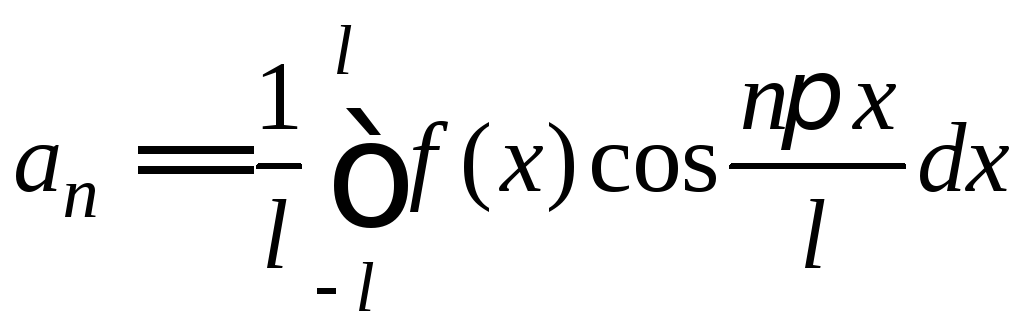 ,
n=0,1,2,…,
,
n=0,1,2,…,
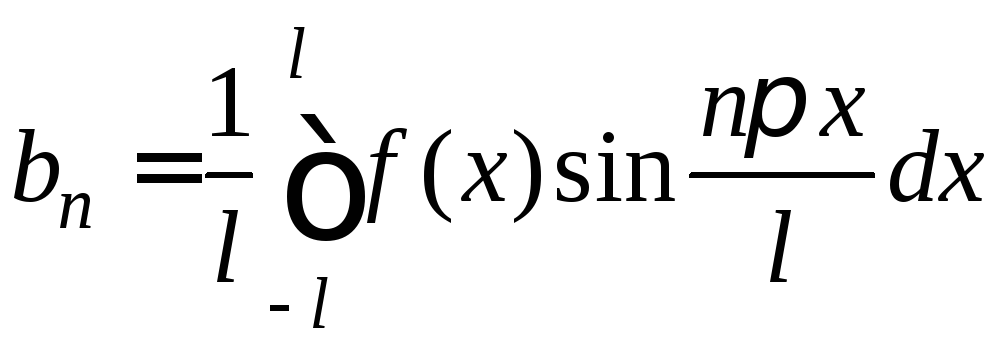 ,
n=1,2,…
,
n=1,2,…
Ввиду простоты изложенного перехода в последующем изложении мы не будем возвращаться к случаю функций, заданных на интервале [-l,l].
Задачи
Нарисовать графики и найти ряды Фурье следующих функций, считая, что они периодичны с периодом 2l:
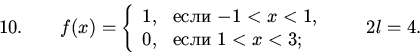
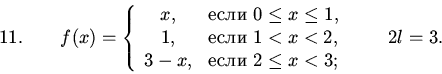
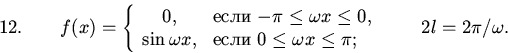
§1.3. Разложения только по синусам или только по косинусам
Начнем со следующего
простого замечания: если заданная в
промежутке
![]() интегрируемая функцияf
нечетна, т.е. для всех
интегрируемая функцияf
нечетна, т.е. для всех
![]() справедливо равенствоf(-x)=-f(x),
то
справедливо равенствоf(-x)=-f(x),
то
 ,
а еслиf(x)
– четная функция, то
,
а еслиf(x)
– четная функция, то
 .
.
Пусть теперь f
является интегрируемой в промежутке
![]() четной
функцией. Тогда произведениеf(x)sinnx
будет нечетной функцией и, по сказанному
выше,
четной
функцией. Тогда произведениеf(x)sinnx
будет нечетной функцией и, по сказанному
выше,
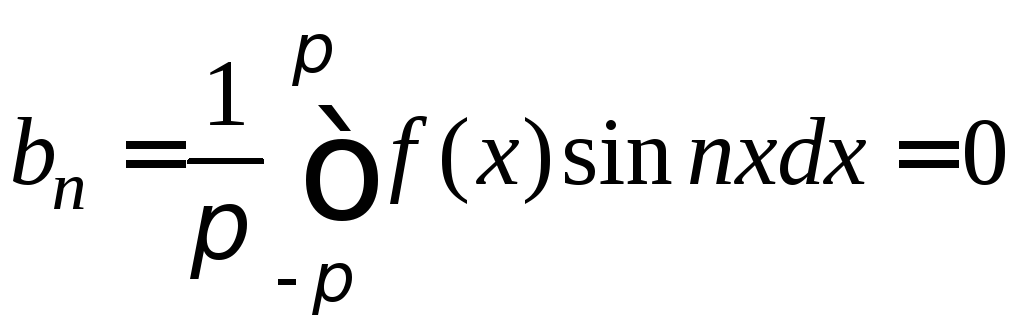 ,
n=1,2,…
,
n=1,2,…
Таким образом, ряд Фурье четной функции содержит только косинусы:

причем коэффициенты an могут быть найдены по формуле
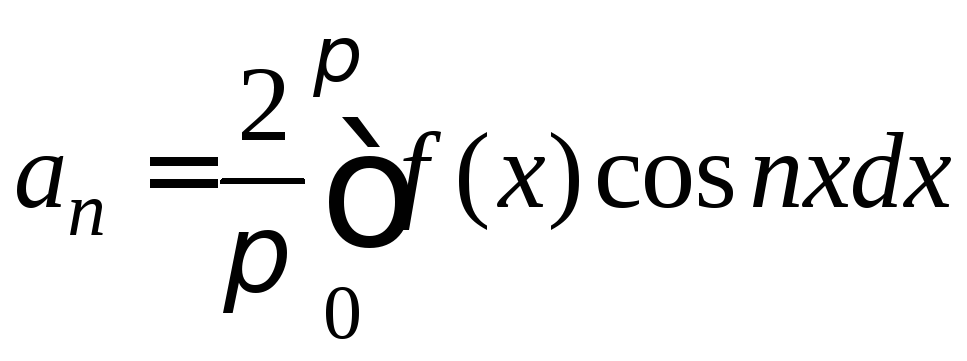 , n=0,1,2,…
, n=0,1,2,…
поскольку функция f(x)cosnx в рассматриваемом случае является четной.
Аналогично, ряд Фурье нечетной функции содержит одни лишь синусы:
 ,
,
а его коэффициенты могут быть записаны в виде
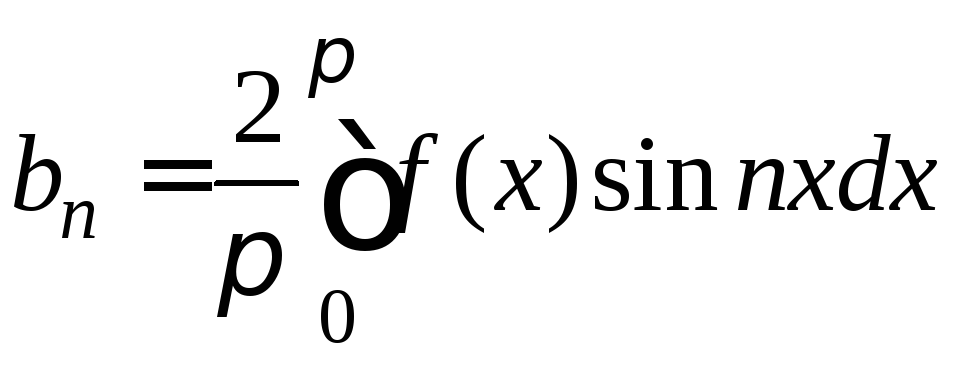 ,
n=1,2,…
,
n=1,2,…
Предположим далее,
что функция f
задана лишь в промежутке [0;].
Желая разложить ее в этом промежутке
в ряд Фурье, мы сначала продолжим f
в промежуток
![]() произвольным образом, а затем воспользуемся
формулами Эйлера - Фурье. Произвол в
продолжении функции приводит к тому,
что для одной и той же функции
произвольным образом, а затем воспользуемся
формулами Эйлера - Фурье. Произвол в
продолжении функции приводит к тому,
что для одной и той же функции![]() мы можем получать различные ряды Фурье.
Но можно использовать этот произвол
так, чтобы получить разложение только
по синусам или только по косинусам: в
первом случае достаточно продолжитьf
нечетным образом, а во-втором - четным.
мы можем получать различные ряды Фурье.
Но можно использовать этот произвол
так, чтобы получить разложение только
по синусам или только по косинусам: в
первом случае достаточно продолжитьf
нечетным образом, а во-втором - четным.
§1.4. Лемма Римана - Лебега
Лемма (Римана - Лебега). Если функция f интегрируема на промежутке [a,b], то
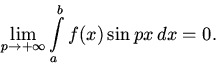
Доказательство.
Если функция f
непрерывно дифференцируема в промежутке
[a,b],
то интегрируя по частям непосредственно
получаем, что при
![]()
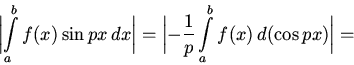
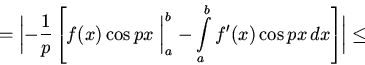
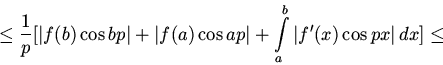
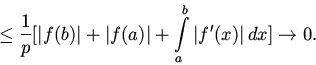
В общем случае
доказательство леммы Римана - Лебега
опирается на следующее утверждение:
если
![]() интегрируема, то для любого
интегрируема, то для любого
![]() найдется
такая непрерывно дифференцируемая
функция
найдется
такая непрерывно дифференцируемая
функция
![]() что
что
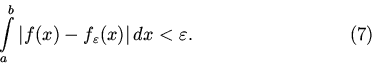
Строгое доказательство этого утверждения потребовало бы от нас вернуться к теории интегрирования, что представляется сейчас неуместным. Поэтому мы примем его без доказательства, ограничившись пояснением на рисунках.
На рис. 1 сплошной линией изображен
график функции
![]() ,а
пунктирной -- график искомой функции
,а
пунктирной -- график искомой функции![]() ,
там, где он не совпадает с графиком
функцииf. При этом значение интеграла
,
там, где он не совпадает с графиком
функцииf. При этом значение интеграла
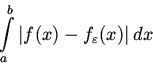
равняется площади заштрихованной области и не вызывает сомнения, что оно действительно может быть сделано меньше любого наперед заданного значения. Рис. 2 иллюстрирует обсуждаемое утверждение для функции f(x)=|x|.
Используем сформулированное выше утверждение для завершения доказательства леммы Римана - Лебега:
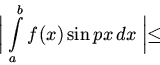

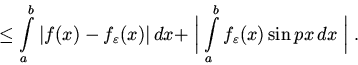
Первое слагаемое
в правой части меньше
![]() в
силу (7), а второе стремится к нулю при
в
силу (7), а второе стремится к нулю при![]() (и, следовательно, также может быть
сделано меньше
(и, следовательно, также может быть
сделано меньше![]() ),
поскольку функция
),
поскольку функция![]() непрерывно дифференцируема. Лемма
доказана.
непрерывно дифференцируема. Лемма
доказана.
В заключение отметим, что для интегрируемой на отрезке [a,b] функции f справедливо утверждение
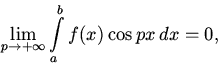
доказательство которого дословно повторяет приведенное выше доказательство леммы Римана - Лебега.
