§1.10. Задача о наилучшем приближении и неравенство Бесселя

Тригонометрическим многочленомn-го порядка называется выражение

Фиксируем nи попробуем найти тригонометрический многочленn-го порядка, наиболее хорошо приближающий данную функциюf.

Прежде всего обсудим, что значит ``наиболее хорошее приближение''. В качестве меры уклонения многочлена T_nот функцииfбыло бы естественно взять величину

и считать, что приближение тем лучше, чем эта величина меньше. Вы работали с этой величиной, когда изучали функциональные ряды и называли ее супремум-нормой  илиC-нормой  функцииT_n-f. Напомним, что эта величина меньшеесли и только если график многочленаT_nлежит в полосе шириной,построенной вокруг графика функцииf. Однако в некоторых задачах за меру уклонения удобнее брать среднее отклонение

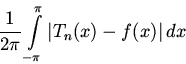
или же среднее квадратичное отклонение

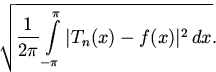
Мы остановимся на последнем варианте, убрав несущественные сейчас корень и постоянный множитель.

Итак, точная формулировка задачи о наилучшем приближении, к решению которой мы и приступаем, такова: среди всех тригонометрических многочленов данного порядка nнайти тот, для которого величина

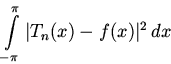
принимает наименьшее значение.

Теорема.Среди всех тригонометрических многочленов данного порядка n величина

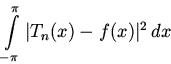
принимает наименьшее значение для того многочлена, коэффициенты которого являются коэффициентами Фурье функции f.

Доказательство.Для начала преобразуем подынтегральное выражение минимизируемого интеграла:

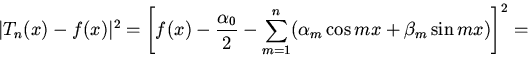
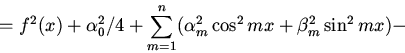
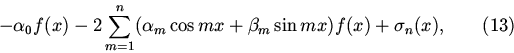
где обозначает линейную комбинацию функций вида,,,,ипри.Поскольку интеграл по промежуткуот каждой из этих функций равен нулю, то.Учитывая еще что,проинтегрируем формулу (13) по промежутку:

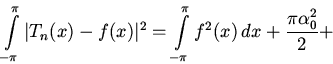
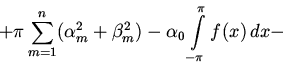
Продолжим преобразования, воспользовавшись формулами Эйлера -- Фурье:

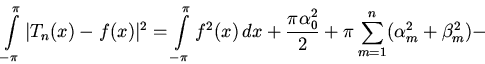
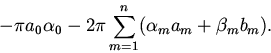
Наконец, выделяя полный квадрат, получим

Первое, третье и пятое слагаемые в правой части равенства (14) не зависят от .Второе и четвертое слагаемые неотрицательны. Значит, интересующий нас интеграл будет принимать минимальное значение если и только если коэффициентывыбраны так, что второе и четвертое слагаемые обращаются в нуль, т.е. если,,.Теорема доказана.

Из равенства (14) вытекает еще одно важное свойство коэффициентов ряда Фурье, называемое неравенством Бесселя.

Теорема(неравенство Бесселя) .Если квадрат функции f интегрируем по промежутку ,то числовой ряд

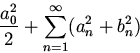
сходится и имеет место неравенство

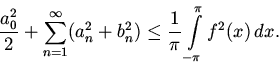
Доказательство.Заменяя в равенстве (14) произвольный многочленT_nчастичной суммой

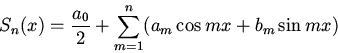
ряда Фурье функции f, получим равенство

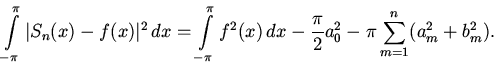
Левая его часть неотрицательная, поскольку мы интегрируем неотрицательную функцию. Значит,

Все члены числового ряда

неотрицательны, а значит, его частичные суммы монотонно возрастают. Но, согласно (15), все они ограничены одним и тем же конечным числом и поэтому имеют конечный предел. Другими словами это означает, что ряд (16) сходится. Переходя к пределу при в неравенстве (15), завершим доказательство теоремы.

§1.13. Гладкость функции и скорость сходимости ее ряда Фурье

Начнем с двух вспомогательных утверждений.

Лемма(неравенство Коши -- Буняковского).Пусть последовательности ивещественных чисел таковы, что ряды

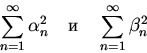
сходятся. Тогда ряд

также сходится и имеет место неравенство

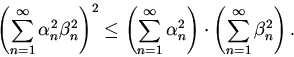
Доказательство.Фиксируем натуральное числоnи рассмотрим сумму

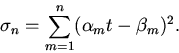
С одной стороны ясно, что для всех справедливо неравенство.С другой стороны, раскрыв скобки, мы получим квадратный трехчлен

где использованы обозначения ,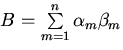и.Как известно, такой трехчлен неотрицателен, если и только если его дискриминант неположителен:

что эквивалентно неравенству

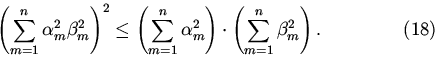
Здесь можно было бы закончить доказательство, сказав что-нибудь вроде ``переходя к пределу при ,получаем требуемое неравенство''. Однако мы продвинемся немного дальше и действительно докажем сходимость ряда (17). При этом уместно опираться на критерий Коши сходимости числовых рядов, утверждающий, что ряд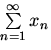сходится, если и только если для каждогонайдется натуральное числотакое, что для всехp>0 ибудет выполнено неравенство

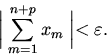
Зададим и, пользуясь тем, что ряд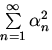сходится, найдем натуральное числотакое, чтобы для всехp>0 ивыполнялось неравенство

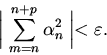
Кроме того, используя сходимость ряда 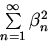,найдем натуральное числотакое, чтобы для всехp>0 ивыполнялось неравенство

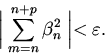
Тогда из неравенства (18) вытекает, что для всех p>0 и

а значит, в силу критерия Коши ряд (17) сходится. Переходя в (18) к пределу, завершим доказательство леммы.

Лемма.Если и,то

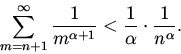
Доказательство.Изобразим члены ряда графически в виде прямоугольников с основанием 1 и высотой(рис. 6). Ясно, что все эти прямоугольники лежат ниже графика функции,а значит, их суммарная площадь не превосходит площади подграфика этой функции, т.е. интеграла от нее:

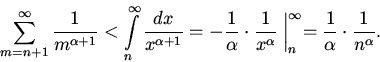
Теорема.Пусть функция -периодична и имеет (k+1)-ю непрерывную производную.Тогда остаток ряда Фурье функции f

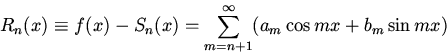
допускает оценку

Доказательство.ПустьA_nиB_nявляются коэффициентами Фурье функцииf^(k+1). Вспоминая теорему о дифференцировании ряда Фурье и меняя, если нужно,A_nиB_nролями, будем иметь

Тогда, используя неравенство Коши -- Буняковского, будем иметь для всех

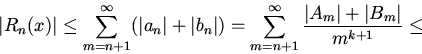
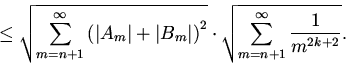
Используя очевидное неравенство и лемму, непосредственно предшествующую данной теореме, продолжим вычисления:

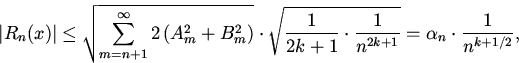
где введено обозначение

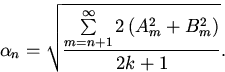
В силу неравенства Бесселя для функции f^(k+1)рядыисходятся. Следовательно, в числителе последнего выражения длястоит хвост сходящегося ряда, который, как известно, стремится к нулю при.Поэтомупри,что и доказывает теорему.

23