Госы 5к Надя / лекции_3 / int_ zaw_ot_ par / Математический анализ - Интегралы - Аксёнов - 2000 - 145

π 2

R

I1 = ∫∫e−x2 −y2 dxdy = ∫∫e−r2 r drdϕ = ∫

dϕ∫e−r2 r dr =

( D1 )

( ∆1 )

0

0

R

R

rr==0R = π4 (1 −e−R2 );

= π2 ∫e−r2 r dr = π4 ∫e−r

2 dr2 = − π4 e−r2

0

0

−x2

−y2

π 2

R

2

−r2

π −r2

r= 2R

π

(

−2 R2

)

∫∫

∫

∫

I3 =

e

dxdy =

dϕ

e

r dr = −

4

e

r=0

=

4

.

1−e

( D3 )

0

0

Теперь неравенство (2) может быть записано в виде

π4 (1 −e−R2 )≤

R

2

(1 −e−2 R2 )

∫e−x2 dx ≤ π4

0

R

π

2

2

π

2

1 −e−R

≤ ∫e−x

dx

≤

1−e−2 R

.

2

2

0

В этом неравенстве перейдем к пределу при R → +∞. Так как

π

1 −e−R2

→

π

,

π

1 −e−2 R2

→

π

,

2

2

2

R→+∞

2

R→+∞

то по теореме о сжатой переменной заключаем, что

R

2

π

Rlim→+∞ ∫e−x

dx =

.

2

+∞

0

0

2

π

2

π

Итак, получили

∫e−x

dx

=

2

. Легко показать,

что

∫e−x

dx =

2

, а следо-

+∞

0

−∞

вательно,

∫e−x2 dx =

π .

−∞

I = ∫∫ f ( x, y) dxdy

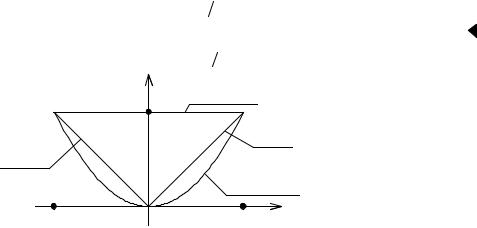
Пример 2. В интеграле

перей-

y

r

= a cosϕ

( D )

ти к полярным координатам и расставить пределы ин-

тегрирования, если (

) – круг x2 + y2 ≤ ax ( a > 0 ).

D

ϕ

x

2

2

a 2

2

a2

a

a

2

x + y ≤ ax

x −

2

+ y ≤ 4 ( D ) –

a

a

круг радиуса 2

с центром в точке

Рис. 3.30. К примеру 2

2 , 0 . Положим

91

x = r cosϕ,

Окружность x

2

+ y

2

= ax в полярных координатах задается урав-

y = r sin ϕ.

нением r

2

= ar cosϕ

π

,

π

J (r,ϕ) = r .

r = a cosϕ, ϕ −

2

. Якобиан

2

Если внешнее интегрирование производить по ϕ, то промежутком измене-

ния

ϕ,

π

,

π

Взяв

произвольное значение

ϕ из

промежутка

будет −

2

2

.

π

,

π

, видим по рисунку 3.30, что r

изменяется от r = 0 до r = a cosϕ. Бу-

−

2

2

дем иметь, следовательно,

π 2

r=a cos ϕ

I =

∫

dϕ

∫ f (r cosϕ,r sin ϕ)r dr .

−π 2

r=0

y

r =

a

Пример

3.

В

интеграле

sin ϕ

a

I =

∫∫ f ( x, y) dxdy

перейти к поляр-

ϕ= π

ϕ=3π

4

( D )

4

sin ϕ

ным координатам и расставить пределы

r =a

cos2ϕ

интегрирования, если (

)

– параболи-

D

x

−a ≤ x ≤ a,

−a

a

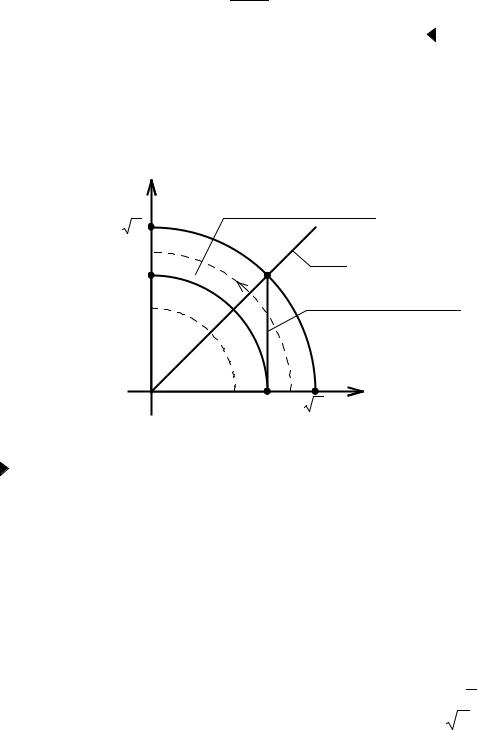
Рис. 3.31. К примеру 3

ческий сегмент x2

≤ y ≤ a.

a

В полярных координатах отрезок прямой y = a , −a ≤ x ≤ a , определяется

уравнением:

r =

a

,

ϕ π

, 3π

, а кусок параболы y =

x2

,

x [−a, a],

–

sin ϕ

4

4

a

уравнением:

r = a

sin ϕ

, ϕ 0,

π U

3π

, π . Будем производить внешнее

cos

ϕ

4

2

4

интегрирование по ϕ.

π

Взяв произвольное значение ϕ из промежутка 0,

4

,

sin ϕ

видим по рисунку 3.31, что r изменяется от r = 0 до r = a

. Взяв произ-

cos2 ϕ

вольное значение ϕ из промежутка π,

3π

, видим, что r

изменяется от r = 0

4

4

до r =

a

. Взяв произвольное значение ϕ из промежутка 3π, π , видим,

sin ϕ

sin ϕ

4

что r изменяется от r = 0 до r = a

. Будем, следовательно, иметь

cos2 ϕ

92

π	r=a	sin ϕ	3π		r=	a
		cos2 ϕ
						sin ϕ
I = ∫4 dϕ		∫ f (r cos ϕ, r sin ϕ)r dr + ∫4		dϕ		∫ f (r cosϕ,r sin ϕ)r dr +
0	r=0		π		r=0
			4

πr=a cossin2ϕϕ

+ ∫ dϕ	∫ f (r cosϕ,r sin ϕ)r dr .
3π	r=0
4

1 1

Пример 4. В интеграле I = ∫dx∫ f ( x, y) dy перейти к полярным координа-

0 0

там и расставить пределы интегрирования в том и другом порядке.
	y		1							1
		r =sin		ϕ
2								ϕ = arcsin r
									π
			C
B								ϕ= 4			1
									1
								r =cosϕ
											ϕ = arccos r

O

A

x

1

2

Рис. 3.32. К примеру 4

Область

интегрирования

(

)

определяется

соотношениями

D

0 ≤ x ≤1,

x = r cosϕ,

J (r,ϕ) = r .

( D ) =

При замене

0 ≤ y ≤1.

y = 0,

y = r sin ϕ,

ϕ = 0,

Отрезок OA =

≤ x ≤

1

≤ r ≤1.

0

0

x = 0,

π

,

ϕ =

2

Отрезок OB =

≤ y ≤

1

0

≤ r ≤1.

0

x =1,

r

=

1

,

1

,

cosϕ

ϕ = arccos

r

Отрезок AC =

≤ y ≤1

π

0

0 ≤ ϕ ≤

1 ≤ r ≤ 2.

4

93

					1
	y =1,		r		=			,
						sin ϕ
Отрезок BC =	≤ x ≤1
0				π	≤ ϕ ≤		π
			4				2

				1	,
	ϕ = arcsin			r
		1 ≤ r ≤	2.

I. Если внешнее интегрирование производить по ϕ, то будем иметь

π		1	π		1
I = ∫4 dϕ	r=cos ϕ			r=sin ϕ
		∫ f (r cosϕ,r sin ϕ)r dr + ∫2 dϕ			∫ f (r cosϕ,r sin ϕ)r dr .
0	r=0		π	r=0
			4

II. Будем производить теперь внешнее интегрирование по r . Взяв произвольное значение r из промежутка [0, 1], видим по рис. 3.32, что ϕ изменяется

от ϕ = 0	до ϕ =	π	. Взяв произвольное значение r из промежутка [1,					2], ви-
		2
дим, что ϕ изменяется от ϕ = arccos				1	до ϕ = arcsin	1	. Будем иметь,	следова-
				r		r

тельно,

1	ϕ=	π
		2
I = ∫dr	∫	f (r
0	ϕ=0

	y
2
1	B
	C

2	1
	ϕ=arcsin r
cos ϕ, r sin ϕ)r dϕ + ∫ dr	∫ f (r cosϕ,r sin ϕ)r dϕ.
1	1
	ϕ=arccosr
	1 y=x2
Пример 5. В интеграле I = ∫dx		∫ f ( x, y) dy
	0	y=0

перейти к полярным координатам и расставить пределы интегрирования в том и другом порядке.

Область интегрирования ( D ) определяет-

		x	ся	соотношениями		0 ≤ x ≤1,	Делаем
	A				( D ) =
O		2			0 ≤ y ≤ x2.
	1			x = r cosϕ,	J (r,ϕ) = r .
	Рис. 3.33. К примеру 5
			замену
				y = r sin ϕ

y = 0,

ϕ = 0,

Отрезок OA =

≤ x ≤

1

≤ r ≤1.

0

0

x =1,

r

=

1

,

1

,

cosϕ

ϕ = arccos

r

Отрезок AB =

≤ y ≤1

π

0

0

≤ ϕ ≤

1 ≤ r ≤ 2.

4

94

sin ϕ

2

2

r =

2

,

1 +

4r

−1

,

ϕ

,

(OCB = y = x

cos

ϕ = arcsin

2r

0 ≤ x ≤1

0 ≤

ϕ ≤

π

0 ≤ r ≤

2.

4

sin ϕ

π

( y = x

2

r sin ϕ = r

2

cos

2

ϕ r =

, ϕ

0,

;

cos

2

ϕ

4

имеем также

r sin ϕ = r2 (1−sin2 ϕ)

r sin2 ϕ +sin ϕ −r = 0

sin ϕ = −1 ±

1 +4r2

π

2r

так как sin ϕ ≥ 0 для ϕ 0,

4

,

sin ϕ =

1 +4r2 −1

ϕ = arcsin

1 +4r2 −1

, r [0,

2].

2r

2r

ϕ(r) в точке r = 0 понимается в предельном смысле, ϕ(0) = 0 .

I. Будем производить внешнее интегрирование по ϕ. Взяв произвольное

значение ϕ из промежутка							π		видим по рис. 3.33, что r		изменяется от
						0,
	sin ϕ						4
r =		до r =	1		. Поэтому будем иметь
	cos2 ϕ		cosϕ
					π		1
						r=
								cos ϕ
				I = ∫4 dϕ				∫ f (r cos ϕ, r sin ϕ)r dr .
					0	r=		sin ϕ
							cos2ϕ

II. Станем производить теперь внешнее интегрирование по r . Взяв произвольное значение r из промежутка [0, 1], видим по рис. 3.33, что ϕ изменяется

от ϕ = 0	до ϕ = arcsin						1 +4r2 −1 . Взяв произвольное значение r из проме-
жутка [1,		2],					2r		1
			видим				по рис. 3.33, что ϕ	изменяется от ϕ = arccos r			до
ϕ = arcsin		1 +4r2 −1			. Следовательно, будем иметь
		2r
1	ϕ=arcsin		1+4r2 −1				2	ϕ=arcsin	1+4r2 −1
				2r					2r
I = ∫dr			∫	f (r cos ϕ, r sin ϕ)r dϕ + ∫ dr					∫ f (r cosϕ,r sin ϕ)r dϕ.
0		ϕ=0					1		1
								ϕ=arccosr

95

Пример 6. Переменить порядок интегрирования в интеграле

π 2

r=a

sin 2ϕ

I = ∫ dϕ ∫ f (ϕ, r) dr .

−1 arcsin r2

0

r=0

y

π

Область интегрирования (

) определяет-

ϕ=

D

2

2

a2

0 ≤ ϕ

≤

π

,

ϕ= π

2

Из

ся соотношениями: ( D ) =

4

0

≤ r ≤ a

sin 2ϕ.

1

r2

2

2

соотношения r = a

sin 2ϕ

r

= a

sin 2ϕ

ϕ= 2 arcsin

a2

x

sin 2ϕ =

r2

2ϕ = arcsin

r2

O

a

a2

a2

Рис. 3.34. К примеру 6

ϕ =

1 arcsin

r

2

, r [0, a]. Требуется произве-

a2

сти внешнее интегрирование по r .

2

Возьмем произвольное значение r

из промежутка [0, a]. Из рис. 3.34 ви-

дим, что ϕ будет изменяться при этом r от значения ϕ =

1 arcsin

r2

до значе-

a2

π

1

r2

2

ния ϕ =

−

arcsin

. Следовательно, будем иметь

2

2

a

2

r2

ϕ=

π

−

1

arcsin

a

2

2

a2

I = ∫dr

∫ f (ϕ,r) dϕ.

0

ϕ=

1

arcsin

r2

2

a

2

Пример 7. В двойном интеграле ∫∫ f ( x, y) dxdy , где ( D ) – область, огра-

( D )

ниченная линиями: x + y = 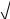a ( a > 0 ), x = 0 , y > 0 , сделать замену пере-

x = ucos4 v,

менных по формулам:

y = usin4 v.

При такой замене:

( a > 0 )

1) линия

x +

y =

перейдет

в

линию

a

u cos2 v +

u sin2 v =

a

u =

u = a (рис. 3.35, 3.36);

a

y = 0,

usin4 v = 0,

v = 0,

2) линия

перейдет в линию

0 < ucos4 v ≤ a

< u ≤ a;

0 < x ≤ a

0

96

	x = 0,		ucos	4	v	= 0,			v =	π	,
										2
3) линия	< y ≤ a	перейдет в линию	< usin4 v ≤ a
0		0							< u ≤ a;
								0

4) точка O(0, 0)		4	v = 0,	u = 0 .
	перейдет в линию ucos
y	usin4 v = 0			v

a

π2

(∆)

(D)

x

u

O

a

O

a

Рис. 3.35. К примеру 7 Рис. 3.36. К примеру 7

J (u, v) =		xu′	xv′		=	cos4 v −4ucos3 v sin v	= 4usin3 v cos3 v .
		yu′	yv′			sin4 v 4usin3 v cos v
Следовательно,		a	v=π 2
I = 4∫u du					∫ f (ucos4 v,usin4 v)sin3 v cos3 v dv .
	0				v=0

Пример 8. Произведя соответствующую замену переменных, свести двой-

ной интеграл	I = ∫∫ f ( x y) dxdy , где (		) – область, ограниченная линиями:
		D
	( D )
xy =1, xy = 2 , y = x , y = 4x ( x > 0 , y > 0 ), к однократному.
y			v

	4	y =4x
	3	(D)
	2		y =x
			xy =2
	1
			xy=1
	1	2	x

Рис. 3.37. К примеру 8

4

3

(∆)

2

1

u

1 2

Рис. 3.38. К примеру 8

97

Делаем замену переменных:

xy = u,

=

u

,

x

v

( u > 0 ,

v > 0 , ибо x > 0 , y > 0 ).

y

= v

=

uv

x

y

При такой замене:

1)

линия xy =1 перейдет в линию u =1;

2)

линия xy = 2 перейдет в линию u = 2 ;

3)

линия y = x перейдет в линию v =1;

4)

линия y = 4x перейдет в линию v = 4 .

x′

x′

1

−1

u

2 uv

2

v

3 2

1

J (u, v) =

u

v

=

=

.

u

2v

yu′

yv′

1 v 1

Будем иметь, следовательно,

2 u

2

v

2

v=4

u=2

2

I = 12 ∫du ∫ f (u) dvv =

12 ∫ f (u)[ln v]vv==14 du = ln 2 ∫ f (u) du.

1

v=1

u=1

1

Пример 9. Найти площадь фигуры, ограниченной линией ( x − y)2 + x2 = a2

( a > 0 ).

v

x − y = u,

Делаем замену

переменных

x = v

x = v,

При такой замене линия ( x − y)

2

+ x

2

= a

2

(∆)

u y

= v −u.

a

( a > 0 ) переёдет в линию u2 + v2 = a2 . Это – окруж-

ность радиуса a с центром в точке (0, 0).

J (u, v) =

xu′ xv′

=

0 1

=1.

Рис. 3.39. К примеру 9

y′

y′

−1 1

u

v

Искомая площадь F

фигуры,

ограниченной линией

( x − y)2 + x2 = a2 ( a > 0 ) будет равна

F = ∫∫dxdy = ∫∫

J (u, v)

dudv = ∫∫dudv = πa2 (кв. ед.).

( D )

( ∆)

( ∆)

Пример 10. Найти площадь фигуры, ограниченной линиями:

( x2 + y2 )2 = 2a2 ( x2 − y2 ); x2 + y2 ≥ a2 .

98

ϕ=5π	y	π
		ϕ= 6
6
	r =a	r=a 2cos 2ϕ
	a	x
		a 2	π
		ϕ=−
ϕ=− 5π			6
6
Рис. 3.40. К примеру 10
Переходим к полярным координатам		x = r cosϕ,		В полярной системе
		y = r sin ϕ.

координат линия ( x2 + y2 )2 = 2a2 ( x2 − y2 ) будет иметь уравнение: r = a 2 cos 2ϕ (это – лемниската), а линия x2 + y2 = a2 – уравнение r = a (это

– окружность). Найдем точки пересечения этих линий. Для этого нужно решить систему:

	2 cos 2ϕ,	2 cos 2ϕ =1	cos 2ϕ = 1	ϕ = ±	π	; ϕ = ±5π .
r = a
r = a			2		6	6

Принимая во внимание симметричность фигуры, станем вычислять площадь ее

части, расположенной в первой четверти. Взяв произвольное значение ϕ из
промежутка		π	, видим из рис. 3.40, что r	при этом ϕ изменяется от значе-
	0,
		6

ния r = a до значения r = a 2 cos 2ϕ . Будем иметь, следовательно,

		π	r=a	2 cos 2ϕ		π				r=a 2 cos 2ϕ		π
1 F =		6				6	r	2			dϕ=1	6	(2a2cos 2ϕ−a2 ) dϕ= a	2		3
			dϕ		r dr =												−
		∫		∫		∫						∫						π
4							2			r=a	2		2		2			6
		0		r=a		0						0
	F = 3 3 − π a2 (кв. ед.).
			3
	Пример 11. Найти площадь фигуры,											ограниченной кривыми			y2 = 2 px ;

y2 = 2qx ; x2 = 2ry ; x2 = 2sy ( 0 < p < q ; 0 < r < s ).

99

	v
y	2s
x2=2sy
x2=2ry		(∆)
y2=2qx
(D)	2r
y2=2px
x		u
O	O 2p
Рис. 3.41. К примеру 11		2q
	Рис. 3.42. К примеру 11

Делаем замену переменных

y2xx2

y

При такой замене:

=u,

=v

		1 3		v		2 3	,
	x = u
			2 3			1 3
								.
	y = u				v

1)ветвь параболы y2 = 2 px перейдет в прямую линию u = 2 p ;

2)ветвь параболы y2 = 2qx перейдет в прямую линию u = 2q ;

3)ветвь параболы x2 = 2ry перейдет в прямую линию v = 2r ;

4)ветвь параболы x2 = 2sy перейдет в прямую линию v = 2s .

1

−2 3

2 3 2 1 3

−1 3

J (u, v) =

3 u

v

3 u

v

= −1

J (u, v)

= 1 .

2 u−1 3v1 3 1 u2 3v−2 3

3

3

Поэтому

3

3

2q

2s

F = ∫∫dxdy = ∫∫

J (u, v)

dudv = 13 ∫ du ∫dv = 43 (q − p)(s −r) .

( D )

( ∆)

2 p

2r

Пример 12. Найти площадь фигуры, ограниченной линиями:

2

y

2

x

2

y

2

x 3

3

3

3

(l ):

+

=1; (l ):

+

= 4 ;

1

a

b

2

a

b

(l ):

x

=

y

;

(l ): 8

x

=

y

( x

> 0, y > 0).

b

b

3

a

4

a

100