Госы 5к Надя / лекции_3 / int_ zaw_ot_ par / Математический анализ - Интегралы - Аксёнов - 2000 - 145

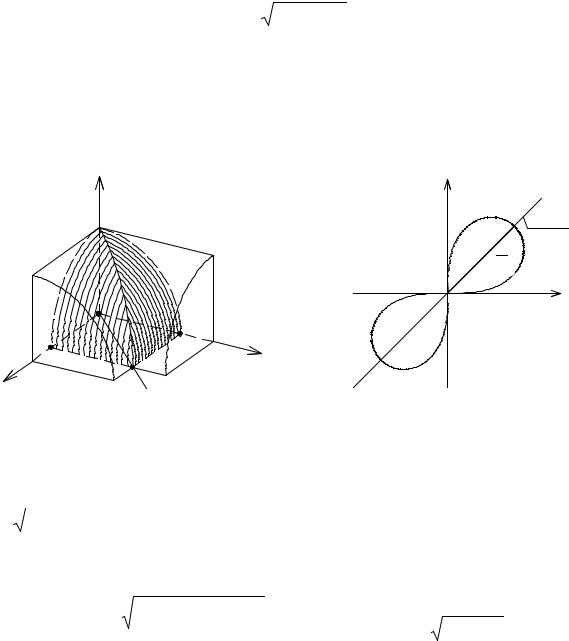
Замечание 2. Положим

( xu′)2 +( yu′)2 +( zu′)2 = E,

( xv′ )2 +( yv′ )2 +( zv′ )2 = G, xu′xv′ + yu′ yv′ + zu′zv′ = F

( E, G, F – это так называемые коэффициенты Гаусса). Легко проверить, что

A2 + B2 + C2 = EG − F2 . Поэтому
		s = ∫∫	EG − F2 dudv .		(11)
		(∆)
		§3. Примеры к главе 4
Пример 1. Найти площадь s			поверхности тела, ограниченного поверхно-
стями: x2 + z2 = a2 ,	y2 + z2 = a2 .		y
z
				y =x
			(D)	x
O	a
a		y
x	y =x
			Рис. 4.7. К примеру 2
Рис. 4.6. К примеру 1

На рис. 4.6 изображена часть интересующей нас поверхности, расположенная в первом октанте. Эта часть поверхности состоит из двух одинаковых по площади кусков. Один из этих кусков определяется уравнением

z = a2 − x2

и

проектируется

на плоскость Oxy

в

треугольник

0 ≤ x ≤ a,

Площадь

~

( D ) =

≤ y ≤ x.

s этого куска поверхности можно определить по

0

−x

~

∫∫

2

2

формуле:

s =

1 +( zx′ )

+( z′y )

dxdy . Имеем:

zx′ =

,

z′y = 0 . Сле-

a2

− x2

( D )

довательно,

x2

a2

1 +( z′ )2

+( z′ )2

=1 +

=

.

x

y

a2 − x2

a2 − x2

А тогда

111

~

a

dx

y=x

a

x dx

2

2 x=a

2

= a∫

2 ∫dy = a∫

= −a a

− x

= a

s

a

2

− x

a

2

− x

2

x=0

.

0

y=0

0

~

1

часть площади s , то находим

Так как s составляет лишь

16

s =16a2 (кв. ед.).

Пример 2. Найти площадь s

части поверхности x2 + y2 = 2az , заключен-

ной внутри цилиндра ( x2 + y2 )2 = 2a2 xy (рис. 4.7).

Поверхность z =

x

2 + y2

– параболоид вращения. Ось Oz

является осью

2a

симметрии

этого

параболоида

вращения.

Цилиндрическая

поверхность

( x2 + y2 )2 = 2a2 xy – симметрична относительно плоскости y = x . Она пересекается с плоскостью Oxy по кривой, уравнение которой в полярных координа-

тах имеет вид: r2 = a2 sin 2ϕ. Одна четвертая часть куска поверхности, вырезаемая цилиндром из параболоида вращения, проектируется на плоскость Oxy

				π			π
	в область ( D ), ограниченную линиями: ϕ =				и r = a sin 2ϕ , ϕ
				4		0,	4	.

Имеем

zx′ = ax ;

Следовательно,

z′	=	y	; 1 +( z′ )2 +( z′ )2				= a2 + x2 + y2
y		a		x		y	a2
	1 +( z′ )2			+( z′ )2	=	a2 + x2 + y2 .
			x	y			a

s = a4 ∫∫ a2 + x2 + y2 dxdy .

( D )

Перейдем в двойном интеграле к полярным координатам. Будем иметь

	4	π 4			r=a sin 2ϕ					2		2					4		π 4			2			2	3 2			r=a	sin 2ϕ
			∫ dϕ ∫																∫
S = a								a			+r		r dr =								(a		+ r		)							dϕ =
																3a													r=0
			0		r=0														0
	4		2	π 4				3 2		−1)dϕ =				4			2		π 4								3
				∫																											π
=	3 a				((1 +sin 2ϕ)									3 a					∫(sin ϕ + cosϕ) dϕ −												4		=
				0															0
						4 2					π 4			3					π					π
					=		a		2		2 ∫		sin		ϕ +								−				=
						3													4	dϕ
											0													4

112

		4 2					π 4					2					π								π			π
	=		a		2	2 ∫			cos					ϕ +										ϕ +			−		=
		3															4		−1 d cos						4
								0																				4
=	4	a	2				−		1		+		1			−		π		=	a2		(20 −3π). (кв. ед.).
	3		2 2					6		2				2				4				9

Пример 3. Найти площадь s части сферы, ограниченной двумя параллелями

и двумя меридианами.	z
Пусть ρ, ϕ, θ – сфериче-

ские координаты точек пространства. Декартовы и сферические координаты точки пространства связаны соотношениями

x = ρcosϕcosθ,y = ρsin ϕcosθ,

z = ρsin θ.

Координаты любой точки сферы радиуса R будут такими:

x = Rcosϕcosθ,y = Rsin ϕcosθ,

z = Rsin θ.

x

θ2

ϕ1 θ1

ϕ2

	Последние уравнения можно	Рис. 4.8. К примеру 3
	рассматривать как параметриче-
	ские уравнения интересующего

нас куска сферы, если ϕ [ϕ1, ϕ2 ]; θ [θ1, θ2 ]. Имеем:

xϕ′

yϕ′

zϕ′

=

−Rsin ϕcosθ

Rcosϕcosθ

0

yθ′

.

xθ′

zθ′

−Rcosϕsin θ −Rsin ϕsin θ

Rcosθ

E = ( x′ )2 +( y′ )2 +( z′ )2 = R2 cos2 θ,

G = ( x′ )2 +( y′ )2

+( z′ )2

ϕ

ϕ

ϕ

θ

θ

θ

F = x′ x′

+ y′

y′

+ z′ z′ = 0

EG − F2 = R2 cosθ.

ϕ

θ

ϕ

θ

ϕ θ

Следовательно,

ϕ2

θ2

s =

∫∫R2 cosθdϕdθ = R2 ∫dϕ∫cosθdθ =

ϕ1

≤ϕ≤ϕ2

ϕ1

θ1

θ1

≤θ≤θ2

= R2 (ϕ

2

−ϕ )(sin θ

2

−sin θ ) (кв. ед.).

1

1

y

= R2 ,

113

Пример 4. Найти площадь части поверхности тора

x = (b +a cosθ)cosϕ,
		< a ≤ b) ,
y = (b +a cosθ)sin ϕ, (0
	z = a sin θ

ограниченной двумя меридианами ϕ = ϕ1 , ϕ = ϕ2 ( ϕ1 < ϕ2 ) и двумя паралле-

лями θ = θ1 , θ = θ2 ( θ1 < θ2 ). Чему равна поверхность всего тора? y

O

C

x

b

a

Рис. 4.9. К примеру 4

Найдем коэффициенты Гаусса данной поверхности. Имеем:

xϕ′

yϕ′

zϕ′

−(b + a cosθ)sin ϕ (b +a cosθ)cosϕ

0

yθ′

=

−a sin θcosϕ

−a sin θsin ϕ

.

xθ′

zθ′

a cosθ

E = ( x′ )2

+( y′ )2 +( z′ )2 = (b +a cosθ)2 ,

G = ( x′ )2 +( y′ )2

+( z′ )2

= a2 ,

ϕ

ϕ

ϕ

θ

θ

θ

F = x′ x′ + y′ y′

+ z′ z′ = 0

EG − F2

= a(b + a cosθ) .

ϕ

θ

ϕ θ

ϕ

θ

∫∫

ϕ2

θ2

s =

EG − F2 dϕdθ = a ∫dϕ∫(b + a cosθ) dθ =

ϕ1

≤ϕ≤ϕ2

ϕ1

θ1

θ1

≤θ≤θ2

θ=θ2 =

= a(ϕ

−ϕ ) (bθ+ a sin θ)

2

1

θ=θ1

= a(ϕ2 −ϕ1 ) [b(θ2 −θ1 ) +a(sin θ2 −sin θ1 )] (кв. ед.).

Чтобы найти площадь поверхности всего тора, нужно в полученное выражение для s подставить значения: ϕ1 = 0, ϕ2 = 2π, θ1 = 0 , θ2 = 2π. Получим

sполн. = 2πa 2πb = 4π2ab (кв. ед.)

114

Глава 5. Несобственные интегралы, зависящие от параметра

§1. Определение равномерной сходимости несобственных интегралов

a ≤ x < +∞,

Пусть функция f ( x, y) задана в области Пусть при каждом

c ≤ y ≤ d.

+∞

закрепленном y из [c, d] несобственный интеграл ∫ f ( x, y) dx сходится. То-

a

+∞

гда ∫ f ( x, y) dx будет представлять собою функцию переменной (параметра)

a

y , определенную в промежутке [c, d] (в дальнейшем будем обозначать эту функцию через I( y) , y [c, d]).

			+∞
Утверждение, что несобственный интеграл ∫ f ( x, y) dx				сходится при каж-
			a
дом y из [c, d], означает следующее: при каждом закрепленном y из [c, d]
	A		+∞
	∫	f ( x, y) dx →	∫ f ( x, y) dx .
	a	A→+∞	a
Следовательно,
	A
+∞			+∞
∫ f ( x, y) dx − ∫		f ( x, y) dx → 0 , или ∫ f ( x, y) dx → 0 .
a	a	A→+∞	A	A→+∞

А это означает, что для каждого y из [c, d] по любому ε > 0 можно указать

+∞

число M > 0 такое, что как только A > M , так сейчас же ∫ f ( x, y) dx < ε.

A

Важно заметить, что число M > 0 выбирается по ε > 0 , и для каждого y из

[c, d] оно будет,	вообще говоря,		своим,		то есть M зависит и от ε, и от y :
M = M(ε, y) .
Если же для любого ε > 0 можно указать число M > 0, зависящее только от
ε (то есть одно	и то же для		всех		y из [c, d]),	такое, что как только
		+∞
A > M , так сейчас же		∫ f ( x, y) dx		< ε сразу для всех		y из [c, d], то несобст-
		A

115

+∞

венный интеграл ∫ f ( x, y) dx называется равномерно сходящимся относи-

a

тельно параметра y на [c, d].

Совершенно аналогично вводится понятие равномерной сходимости несобственных интегралов второго рода. Например, пусть функция f ( x, y) опреде-

a ≤ x < b,	( a, b, c, d – конечные числа).
лена в области
c ≤ y ≤ d.	b

Пусть при каждом y из [c, d] несобственный интеграл ∫ f ( x, y) dx сходит-

a

b

ся. Ясно, что тогда ∫ f ( x, y) dx будет представлять собой функцию переменной

a

(параметра) y , определенную в промежутке [c, d].

b

Утверждение, что несобственный интеграл ∫ f ( x, y) dx сходится при каж-

						a
дом y из [c, d], означает следующее. При каждом закрепленном y из [c, d]
β		b			b	β
∫	f ( x, y) dx →	∫ f ( x, y) dx ∫ f ( x, y) dx − ∫					f ( x, y) dx → 0
a	β→b−0	a			a	a	β→b−0
	b					b
	∫ f ( x, y) dx → 0					∫ f ( x, y) dx→0
	β			β→b−0		b−γ	γ→+0
(здесь положено β = b − γ				γ = b −β). А это означает, что для каждого y из
[c, d]	по любому ε > 0			можно указать		число δ > 0 такое, что как только
				b
0 < γ < δ, так сейчас же				∫ f ( x, y) dx	< ε.
			b−γ

И здесь важно отметить, что число δ > 0 выбирается по ε > 0 , и для каждого y из [c, d] оно будет, вообще говоря, своим, то есть δ зависит и от ε, и от y :

δ = δ(ε, y) .

Если же для любого ε > 0 можно указать число δ > 0 , зависящее только от

ε (то есть одно и то же для всех y из [c, d]), такое, что как только 0 < γ < δ,

b

так сейчас же ∫ f ( x, y) dx < ε сразу для всех y из [c, d], то несобственный

b−γ

116

b

интеграл ∫ f ( x, y) dx называется равномерно сходящимся относительно па-

a

раметра y на [c, d].

§2. О непрерывности интеграла как функции параметра

Теорема. Пусть

a ≤ x < +∞,

1) функция f ( x, y) непрерывна в области c ≤ y ≤ d;

+∞

2) ∫ f ( x, y) dx = I( y) сходится равномерно относительно y на [c, d].

a

Тогда функция I( y) непрерывна на [c, d].

Возьмем любое y0 из [c, d] и закрепим его. Возьмем любое ε > 0 .

+∞

По условию ∫ f ( x, y) dx сходится равномерно относительно y на [c, d],

a

поэтому взятому ε > 0 отвечает число M > 0, зависящее только от ε, такое, что при всяком A, удовлетворяющем условию A > M , сразу для всех y [c, d] бу-

дет

	+∞			ε
	∫ f ( x, y) dx		<
				3 .	(1)
	A				A > M .
Выберем и закрепим какое-нибудь A, удовлетворяющее условию

A

Положив ΨA( y) = ∫ f ( x, y) dx , неравенство (1) сразу для всех y [c, d] можно

a
записать в виде:				ε .
	I( y) − Ψ ( y)		<		(2)
	A			3
+∞	A			+∞
[I( y) −ΨA( y) = ∫ f ( x, y) dx − ∫ f ( x, y) dx = ∫ f ( x, y) dx].
a	a			A

Но ΨA( y) – собственный интеграл, зависящий от параметра y . По теореме о непрерывности собственных интегралов, зависящих от параметра, заключаем, что ΨA( y) C([c, d]), а значит, по теореме Кантора, ΨA( y) будет равномерно непрерывной на [c, d].

Следовательно, взятому ε > 0 отвечает δ > 0 , зависящее только от ε, такое,

117

что для любых двух точек y′ и y′′ из [c, d], для которых							y′′− y′		< δ, будет
	Ψ ( y′′) − Ψ ( y′)			<	ε .
	A	A			3
	Для разности значений функции I( y) в точках y′ и y′′					имеем:

I( y′′) − I( y′) =[I( y′′) − ΨA( y′′)]+[ΨA( y′′) − ΨA( y′)]+[ΨA( y′) − I( y′)]I( y′′) − I( y′) ≤ I( y′′) − ΨA( y′′) + ΨA( y′′) − ΨA( y′) +

+

Ψ ( y′) − I( y′)

<

ε +

ε

+ ε = ε.

A

3

3

3

В частности, полагая y′ = y0 , y′′ = y ,

где

y [c, d] – любое, но такое, что

y − y0

< δ, будем иметь

I( y) − I( y0 )

< ε. Последнее означает, что функция

I( y) непрерывна в точке

y0 . Так как у нас точка y0 – любая из [c, d], то

заключаем, что I( y) C([c, d]).

§3. Об интегрировании по параметру под знаком интеграла

Теорема. Пусть

a ≤ x < +∞,

1) функция f ( x, y) непрерывна в области c ≤ y ≤ d;

+∞

2) ∫ f ( x, y) dx сходится равномерно относительно y на [c, d].

a

Тогда справедливо равенство

d +∞			+∞ d
	∫		∫			(1)
∫		f ( x, y) dx dy =		∫	f ( x, y) dy dx ,
c	a		a	c

причем несобственный интеграл, стоящий в правой части (1), сходится.

+∞

Возьмем любое ε > 0 . По условию ∫ f ( x, y) dx сходится равномерно от-

a

носительно y на [c, d], поэтому взятому ε > 0 отвечает число M > 0, завися-

щее только от ε, такое, что при всяком A, удовлетворяющем условию A > M , сразу для всех y [c, d] будет справедливо неравенство:

+∞

∫ f ( x, y) dx < d ε−c .

A

Выберем и закрепим какое-нибудь A, удовлетворяющее условию A > M .

118

A

Полагая, как и раньше,

ΨA( y) = ∫ f ( x, y) dx , предыдущее неравенство сразу

a

для всех y [c, d] можно записать в виде

I( y) − Ψ ( y)

<

ε

.

A

d −c

Так как

I( y) C([c, d]) и

ΨA( y) C([c, d]), то I( y) R([c, d]),

ΨA( y) R([c, d]). Поскольку имеет место равенство

d

d

d

∫I( y) dy − ∫ΨA( y) dy = ∫[I( y) − ΨA( y)]dy ,

то

c

c

c

d

d

d

ε

∫I( y) dy − ∫ΨA( y) dy

≤ ∫

I( y) − ΨA( y)

dy <

(d −c) = ε.

d −c

c

c

c

A > M ,

Таким образом, получили: при любом A, удовлетворяющем условию

d

d

оказывается

∫I( y) dy − ∫ΨA( y) dy

< ε. Последнее означает, что

c

c

d

d

∫I( y) dy = Alim→∞ ∫ΨA( y) dy

(2)

c

c

A

(именно так, ибо первый интеграл от A не зависит). Но ΨA( y) = ∫ f ( x, y) dx –

a

собственный интеграл, зависящий от параметра y . По теореме об интегрировании по параметру под знаком собственного интеграла можем написать

d	d A		A d
∫ΨA( y) dy = ∫ ∫		f ( x, y) dx dy = ∫ ∫		f ( x, y) dy dx .
c	c a		a c

Теперь соотношение (2) может быть записано в виде

d		A d
∫I( y) dy =	lim
		∫ ∫
c	A→∞ a c

f ( x, y) dy dx .

Нами установлено существование написанного здесь предела. Но тогда мы должны обозначать этот предел так:

+∞ d
∫
	∫	f ( x, y) dy dx .
a	c

Таким образом, мы доказали сходимость несобственного интеграла, стояще-

119

го в правой части (1), и справедливость равенства (1).

§4. О дифференцировании по параметру под знаком интеграла

Теорема. Пусть

				a ≤ x < +∞,		непрерывна там и
1) функция f ( x, y) определена в области
				c ≤ y ≤ d,
имеет непрерывную частную производную f y′( x, y) ;
	+∞
2)	I( y) = ∫ f ( x, y) dx сходится при каждом y из [c, d];
	a
	+∞
3)	Ψ( y) = ∫ f y′( x, y) dx сходится равномерно относительно y на [c, d].
	a
Тогда:
1)	I′( y) существует при каждом y из [c, d];
	+∞		′	+∞
2)				= ∫ f y′( x, y) dx ;
	I′( y) = Ψ( y) , то есть	∫ f ( x, y) dx
		a	y	a
3)	I′( y) C([c, d]).
				a ≤ x < +∞,		+∞
	Так как f y′( x, y) непрерывна в области c ≤ y ≤ d				и	∫ f y′( x, y) dx схо-
						a
дится равномерно относительно			y на [c, d], то Ψ( y) C([c, d]) (см. теорему
	d			z

§2) и ∫Ψ( y) dy существует. В частности, существует ∫Ψ( y) dy для любого z ,

c									c
удовлетворяющего условию c ≤ z ≤ d . По теореме §3 имеем
z	z +∞						+∞ z
∫Ψ( y) dy = ∫				∫
					f y′( x, y) dx dy = ∫			∫	f y′( x, y) dy dx .
c	c			a			a	c
z			yy==cz
Но ∫ f y′( x, y) dy = f ( x, y)					= f ( x, z) − f ( x, c) . Поэтому
c
z			+∞			+∞
∫Ψ( y) dy = ∫ f ( x, z) dx − ∫ f ( x,c) dx = I( z) − I(c),
c				a		a
		14243				14243
					=I( z )		=I(c)

откуда

120