Госы 5к Надя / лекции_3 / int_ zaw_ot_ par / Математический анализ - Интегралы - Аксёнов - 2000 - 145

§6. Вычисление двойного интеграла в случае криволинейной области

Пусть ограниченная функция f (x, y) задана в области (D ), огра-

ниченной	линиями:	y = c , y = d
( c < d ) и	x = α( y);	x = β( y) , где

α( y), β( y) – функции, непрерывные на промежутке [c, d] и такие, что

α( y) ≤β( y) , y [c, d].

Определение. Пусть при каждом закрепленном y из [c, d] существует

y

d

	(D)
c	x =β( y)
x =α( y)	x

β( y)

β

( y)

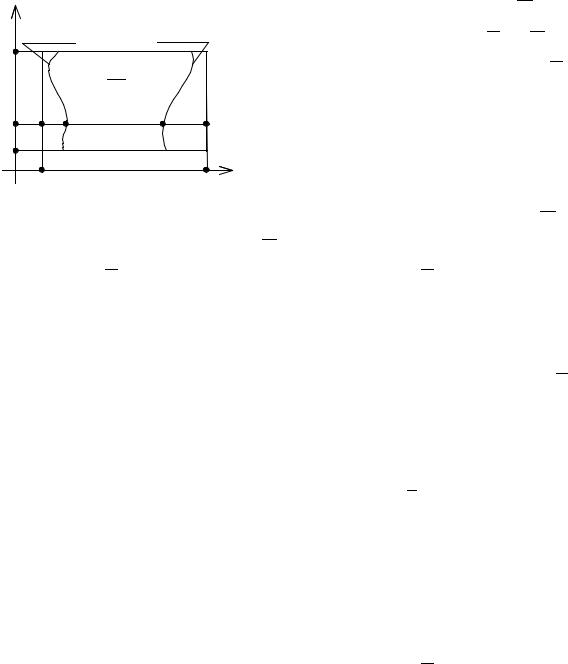
Рис. 2.5. К определению повторного

∫ f (x, y) dx .

Тогда

∫ f (x, y) dx

интеграла от функции

f (x, y)

α( y)

α( y)

в области (

)

D

представляет собой функцию аргу-

мента

y , определенную

на

проме-

β( y)

жутке [c, d], т. е. ∫ f (x, y) dx =

ϕ( y) ,

y [c, d]. Если эта функция ϕ( y)

α( y)

обозн.

[c, d],

оказывается

интегрируемой

на

промежутке

то

d

d

β( y)

∫ϕ( y) dy = ∫dy

∫ f (x, y) dx

называется повторным интегралом от функции

c

c

α( y)

f (x, y) в области (

).

D

Теорема 1. Если у ограниченной функции			f (x, y), заданной в области (		D	),
существуют	одновременно	оба интеграла:		Iдв. = ∫∫ f ( x, y) dxdy		и
				( D )
d	β( y)
Iповт. = ∫dy	∫ f (x, y) dx , то они равны, т. е.		Iдв. = Iповт..
c α( y)
По условию α( y) и β( y)		– функции, непрерывные на [c, d]. Значит, они

– ограниченные на [c, d]. Следовательно, найдутся числа a и b такие, что будет: a < α( y) ≤β( y) < b , y [c, d]. Построим прямоугольник

(		) = a ≤ x ≤ b,	Ясно, что (		) (		). Введем в рассмотрение вспомогатель-
	P			D		P
		c ≤ y ≤ d.

ную функцию g( x, y) , определив ее в прямоугольнике (P ) следующим образом:

41

y

g(x, y) =

f ( x, y) в (D ),

d x =α( y)

x =β( y)

0 в ( P ) \ (D ).

(D)

Покажем, что у функции g( x, y) в (P ) сущест-

y

вуют

оба

интеграла

Iдв*

. = ∫∫g(x, y) dF

и

( P )

c

x

Iповт* .

d

b

a

b

=

∫

dy

∫

g(x, y) dx .

Рис. 2.6. К доказательству

c

a

g( x, y) R( D ),

1) Действительно,

ибо

в

теоремы 1

(D )

g(x, y) ≡ f ( x, y) .

Кроме

того,

g(x, y) R (P ) \ (D)

, ибо g(x, y) = 0

всюду в

(P ) \ ( D) ,

за исключением,

(

)

лежащих на двух простых кривых: x = α( y)

быть может, множества точек,

и

x = β( y) ,

y =[c, d] (мы знаем, что существование и величина двойного инте-

грала не зависят от значений, принимаемых подынтегральной функций вдоль

конечного

числа

простых

кривых). Значит,

g(x, y) R(P ),

т. е.

Iдв*

. = ∫∫g(x, y) dF существует. Имеем, далее,

( P )

Iдв*

. = ∫∫g( x, y) dF = ∫∫g( x, y) dF + ∫∫g( x, y) dF =

( P )

( D )

( P )\( D)

1442443

= ∫∫ f ( x, y) dF + 0 = Iдв. .

=0

( D )

Итак, Iдв*

. существует, и

Iдв*

. = Iдв..

(1)

2) Покажем теперь, что у функции

g( x, y) в (P )

существует I*

. Для

этого возьмем любое y из [c, d] и закрепим его. Имеем

повт.

[a,b] =

[

a,α( y) U

[

α( y),β( y) U β( y),b .

]

]

[

]

Функция g( x, y)

интегрируема по x на каждом из этих трех промежутков, ибо

на

[

α( y),β( y) она совпадает с

f (x, y), а на остальных двух – g(x, y) = 0 всю-

]

ду за исключением, быть может, двух точек. Имеем, далее,

b

α( y)

β( y)

b

β( y)

∫g(x, y) dx = ∫g(x, y) dx + ∫g(x, y) dx + ∫g(x, y) dx = ∫ f (x, y) dx .

a

a

α( y)

β( y)

α( y)

142443

142443

=0

=0

42

По условию, правая часть последнего равенства интегрируема на промежутке [c, d] (по условию, Iповт. существует). Значит, интегрируема на промежутке

		т. е. существует Iповт*	d	b
[c, d] и левая часть этого равенства,			. = ∫dy∫g(x, y) dx .
Таким образом, показано, что Iповт*			c	a
	. существует и что
Iповт*		. = Iповт..		(2)

Так как у ограниченной функции g( x, y) , заданной в прямоугольнике (P ), су-

ществуют оба интеграла I*			и I*		, то по теореме 1 предыдущего параграфа
		дв.		повт.
заключаем, что				I*	= I* .
								(3)
				дв.	повт.
У нас Iдв*	. = Iдв., Iповт*	. = Iповт.. Следовательно, Iдв. = Iповт..
								β( y)
Теорема 2. Пусть функция				f (x, y) C(			) , и пусть ϕ( y) =	∫ f ( x, y) dx ,
						D
								α( y)

y [c, d]. Тогда ϕ( y) C([c, d]).

Эта теорема была доказана ранее (см. гл. 1, §6, теорема о непрерывности

интеграла как функции параметра).
Следствие. Если функция	f (x, y) C(		) , то существует
		D
d	d			β( y)
Iповт. = ∫ϕ( y) dy = ∫dy				∫ f (x, y) dx .
c	c α( y)
Ранее (см. §3, теорема 2)	было доказано, что если f (x, y) C(					) , то
					D

f (x, y) R(D ) , т. е. существует Iдв. = ∫∫ f ( x, y) dxdy . Таким образом, прихо-

				( D )
дим к заключению: если	f (x, y) C(				) ,	то существуют одновременно Iдв. и
				D
Iповт. . А тогда по теореме 1 настоящего параграфа приходим к выводу, что
Iдв. = Iповт., т. е.
				d		β( y)
∫∫ f ( x, y) dxdy = ∫dy ∫ f ( x, y) dx .								(4)
( D )				c		α( y)
Замечание 1. Если область (			) представляет собой криволинейную трапе-
		D
цию другого типа и ограничена кривыми						~	~	x [a,b] и пря-
						y = α(x),	y = β(x) ,
мыми x = a , x = b , a < b	~					~	предполагаются непрерыв-
	(функции α(x)					и β(x)

43

ными на промежутке [a,b] и такими, формулы (4) придем к формуле

∫∫ f ( x, y) dxdy =

( D )

что	~	~
	α(x) ≤ β(x) ,
b	~
	β( x)
∫dx	~ ∫ f ( x, y) dy .
a	α( x)

x [a,b]), то вместо

(5)

Разумеется, что при этом предполагается, что f (x, y) C(D ) , а, следователь-

но, Iдв. = ∫∫ f ( x, y) dxdy

	( D )
y	~
	y =β(x)

	b	~
~		β( x)
		~ ∫ f ( x, y) dy
и Iповт. = ∫dx
	a	α( x) y

d

существуют.

~

y =β(x)

(D )	(D )

	~	x	c
a	y =α( x)		a
	b

~

y =α( x)

x

b

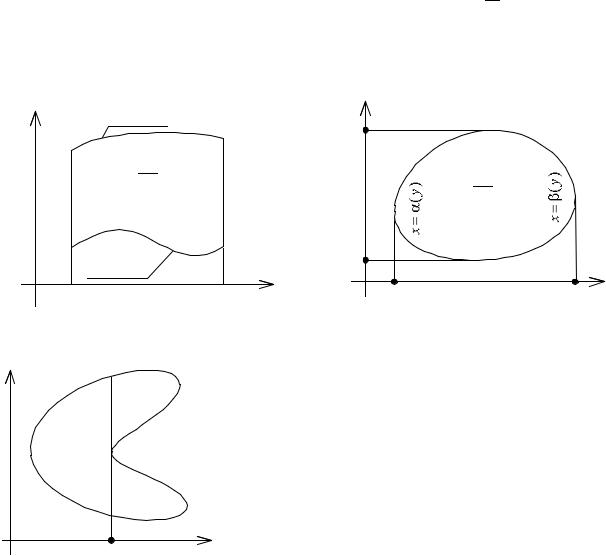
Рис. 2.7. К замечанию 1

Рис. 2.8. К замечанию 2

y

Замечание 2. Если контур области (

) пересе-

D

кается лишь в двух точках как параллелями оси

(D3)

абсцисс, так и параллелями оси ординат (как, на-

пример, в случае, изображенном на рис. 2.8), то

(D1)

справедливы обе формулы (4) и (5). При этом, ко-

нечно, предполагается, что f (x, y) C(

) . Функ-

D

(

D

)

~

~

2

x

ции

α(x), β( x) C([a,b]).

Функции

γ

α( y),β( y) C([c, d]).

Замечание 3. В случае более сложного контура

Рис. 2.9. К замечанию 3

область (

) обычно разлагается на конечное число

D

частей рассмотренного типа (например, на рис. 2.9 область (

) рассекается

D

прямой x = γ на три такие части: (

(

D1 ),

D2 ), ( D3 ) ). Тогда и искомый двойной

интеграл представляется суммой двойных интегралов, распространенных в от-

дельности на эти части:

∫∫ f ( x, y) dF = ∫∫ f (x, y) dF + ∫∫ f ( x, y) dF + ∫∫ f ( x, y) dF .

( D )	( D1 )	(			(
			D2 )			D3 )

44

§7. Примеры к главе 2

1. Вычислить I = ∫∫(x2 + y) dxdy , где (D ) – область, ограниченная двумя

( D )

параболами: y = x2 и y2 = x .

Полезно сделать чертеж (хотя бы грубо), чтобы получить общее представление об области. Решая совместно уравнения парабол, находим точки их пересе-

чения: (0, 0) и (1,1) .

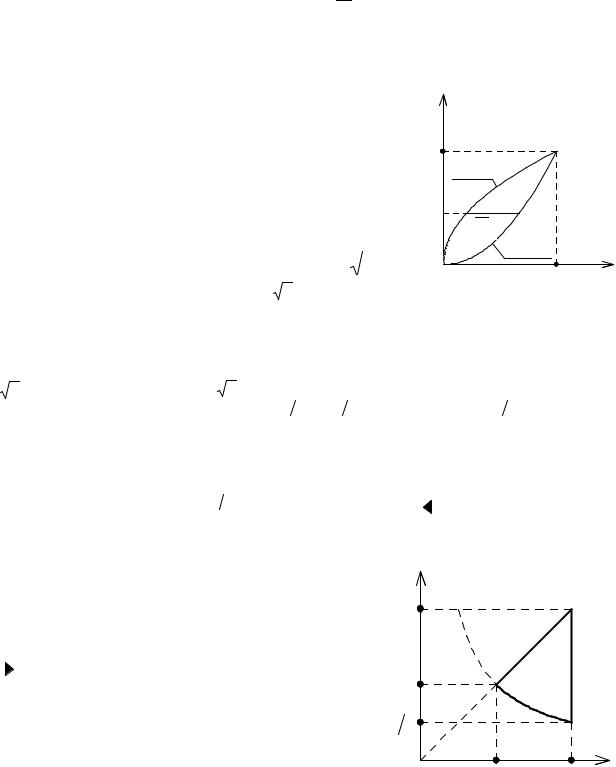
Если внешнее интегрирование производить по y , то промежутком изменения y будет [0,1]. Взяв произвольное значение y из промежутка [0,1], видим по

рисунку, что x изменяется от x = y2		до x =		. Бу-
			y
1	x=	y
дем иметь, следовательно, I = ∫dy	∫(x2 + y) dx .
0	x=y2

y

1	x = y2
y	(D)
		y =x2	x

O 1

Рис. 2.10. К примеру 1

Вычисляем внутренний интеграл:

x= y 2

x3

x= y

1

3 2

3 2

1

6

3

4

3 2

1

6

3

∫

(x

+ y) dx =

+ yx

=

y

+ y

−

y

− y

=

y

−

y

− y

.

3

3

3

3

3

2

x=y2

x

=y

Вычисляем теперь внешний интеграл:

1 4

3 2

1

6

3

33

∫

− 3 y

− y

3 y

dy = 140 .

0

2

2. Вычислить

I = ∫∫

x

dxdy ,

где (

)

– об-

y

D

2

( D ) y

y = x

2

ласть, ограниченная прямыми x = 2 ,

и ги-

y =x

перболой xy =1.

x =2

Наносим

все

эти

три

линии

на

рисунок

1

( D )

(рис. 2.11). Совместным решением

уравнений

легко получить, что прямая

x = 2

пересекает

1 2

xy =1

прямую

y = x

в точке (2, 2),

а гиперболу xy =1

x

1

; прямая же

y = x

и гипербола

O

1

2

– в точке 2,

2

Рис. 2.11. К примеру 2

xy =1 (в пределах первого квадранта, где и лежит

рассматриваемая область) пересекаются в точке (1,1) .

45

Если внешнее интегрирование производить по x , то промежуток изменения x будет [1, 2]. Взяв произвольное значение x из этого промежутка, видим по

рисунку,

что

y изменяется от

y =

1

до

y = x .

Будем иметь, следовательно,

2

y=x

y=x

x

y=x

x

2

x

2

x

2

I = ∫dx

∫

dy .

Но

∫

dy = −

= x3 − x ,

так

что

y

2

y

2

y

1

y=1 x

y=1 x

y=1

2

x

3

9

I = ∫

( x

− x) dx = 4 .

1

В то время как в примере 1 вычисление двойного интеграла по обеим формулам (4) или (5) представлялось одинаково простым, в примере 2 дело обстоит иначе: вычисление по формуле (4) здесь было бы сложнее. Тем не менее мы выполним его, ибо поучительно дать себе отчет в причине указанного обстоятельства.

Прямая, параллельная оси Ox , пересекает контур области (D ) в двух точках, так что формула (4) применима. Но кривая, ограничивающая нашу область слева, состоит из двух частей: куска гиперболы и куска прямой, которые определяются различными уравнениями. Иными словами, функция x = α( y) зада-

ется различными формулами в различных частях промежутка 12 , 2 изменения y . Именно,

	1			y	1
		,	если			, 1 ,
α( y) = y					2
			если	y [1, 2].
y,

Поэтому интегрирование по y следует разбить на два промежутка:

[1, 2]. Следовательно, будем иметь:

1

x=2

x

2

2

x=2

x

2

I = ∫

dy ∫

dx + ∫dy ∫

dx .

y

2

y

2

1 2

x=1 y

1

x=y

Так как

x=2

x=2

x=2

x2

x3

8

1

x=2

x2

x3

8

∫

dx =

=

−

,

∫

dx =

=

2

2

3y

2

3y

5

2

2

3y

2

x=1 y

y

3y

x=

1

x=y

y

3y

x=y

y

то

1 ,1 и2

− 3y ,

46

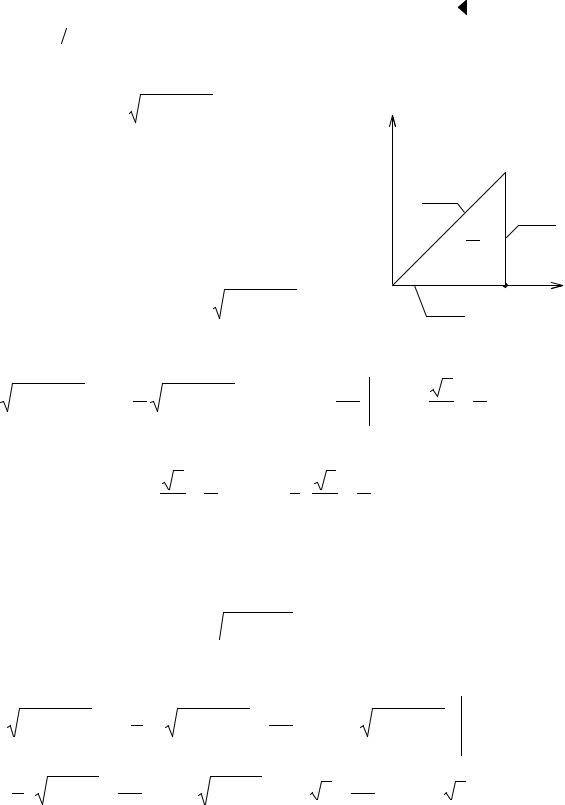
1		8			1			2		8			y		17		5		9
I = ∫				−			dy + ∫					−		dy =		+		=		.
		3y	2		3y	5					2		3		12		6		4
1 2								1	3y

С подобными обстоятельствами приходится считаться: из двух возможных путей вычисления двойного интеграла, естественно, выбирают более простой.

3. Вычислить I = ∫∫ 4x2 − y2 dxdy , где	(		)	–
		D
( D )	y = x .
область, ограниченная прямыми y = 0 , x =1,				x ,
Если внешнее интегрирование производить по

то промежуток изменения x будет [0,1]. Взяв произвольное значение x из промежутка [0,1], видим по

рисунку, что y изменяется от	y = 0 до y = x . Будем
1	y=x
иметь, следовательно, I = ∫dx	∫ 4x2 − y2 dy . Вы-
0	y=0

y

1 y =x

x =1

(D) x

O

y =0

1

Рис. 2.12. К примеру 3

числяем внутренний интеграл:

y=x		2		2	y				2			2				2			y y=x				3		π		2
∫	4x		− y					4x		− y			+ 2x				arcsin							+				.
					dy =	2																=	2		3	x
y=0																			2x		y=0
Вычисляем теперь внешний интеграл:
					I =	1		3	+		π			2	dx	=	1	3	+	π
						∫		2			x							2		3	.
											3						3
						0

В примере 3 вычисление I можно было вести и по формуле (4), т. е. производить внешнее интегрирование по y . Но в этом случае мы натолкнемся на

более трудные квадратуры. Чтобы убедиться в этом, станем вычислять I

1 x=1

по формуле (4). Имеем: I = ∫dy ∫ 4x2 − y2 dx . Вычисляем внутренний инте-

0 x=y

грал:

x=1

2

2

1

2

2

y2

∫

4x

− y

dx =

− y

2

x 4x

−

2 ln (2x + 4x

x=y

1

4 − y

2

y2

4 − y

2

)− y

2

3 +

y2

=

2

−

2 ln (2 +

2 ln

2− y2 ) x=1 =

x=y

(2 y +
	3y) .

А тогда

47

I =	1	1		4 − y	2	−	3y	2	+	ln (2 +	3)	y	2	+	y2	ln		y
	2	∫								2					2						2	dy .
		0														2	+	4	− y
Сопоставляя это выражения для										I с ранее полученным:								I =	1			3	+	π		2	dx ,
																			∫		2			3	x
видим, что вычисление I																			0
							по формуле (5) предпочтительнее. Подобное обстоя-

тельство следует учитывать при выборе формулы для вычисления двойного интеграла.

Для приобретения навыков в расстановке пределов интегрирования в случае

	криволинейной области полезны следующие упражнения.
			y		Задача 1. Переменить порядок интег-
			8		рирования		в	повторном	интеграле
					2	y=2−x
					I = ∫dx ∫ f (x, y) dy .
			x =2 y +1		−6	x2
						y= 4	−1		(D ) опре-
	x = −2 y +1	( D )	2		Область интегрирования
				x	деляется	совместными неравенствами:
	−6	−2	2		−6 ≤ x ≤ 2 ,		x2 −1 ≤ y ≤ 2 − x .		Изобразим
			−1				4
	Рис. 2.13. К задаче 1				эту область		(D )	на рисунке. Из рис. 2.13

видим, что если брать внешнее интегрирование по y , то область (D ) следует разбить на две области (D1 ) и (D2 ) лини-

ей

y = 0 . Тогда:

(

будет

определяться неравенствами:

−1 ≤ y ≤ 0 ,

D1 )

−2

y +1 ≤ x ≤ 2

,

а

(

–

неравенствами

0 ≤ y ≤ 8 ,

y +1

D2 )

−2

y +1 ≤ x ≤ 2 − y . Будем иметь, следовательно,

0

x=2 y+1

8

x=2−y

I = ∫dy

∫ f (x, y) dx + ∫dy

∫ f ( x, y) dx .

−1 x=−2 y+1

0

x=−2 y+1

Задача 2. Переменить порядок интегрирования в повторном интеграле

1

y=1−x2

I = ∫dx

∫ f (x, y) dy .

−1

y=−

1−x2

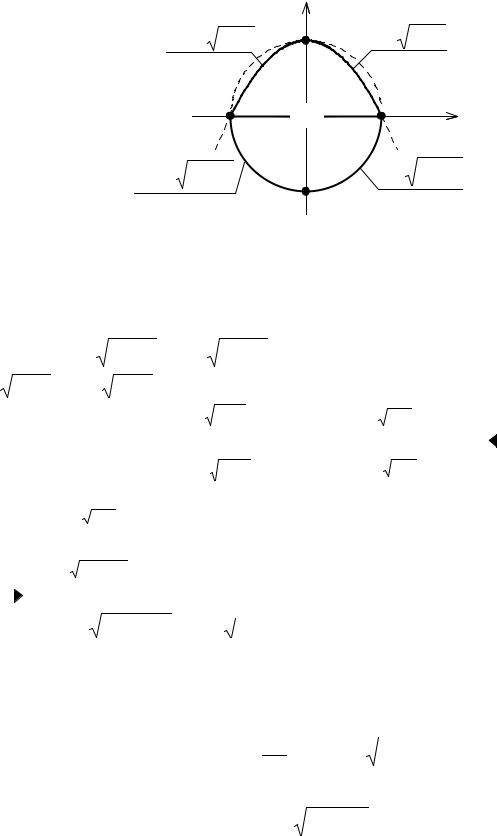
Область интегрирования (D ) определяется совместными неравенствами

−1 ≤ x ≤1, − 1 − x2 ≤ y ≤1− x2 .

48

y

x =− 1− y

1

x = 1− y

−1

1

x

( D )

x =− 1− y2

−1

x = 1− y2

Рис. 2.14. К задаче 2

Изобразим область (

) на рисунке. Из рис. 2.14 видим, что если внешнее ин-

D

тегрирование производить по

y , то область (

) следует разбить линией y = 0

D

на две области (

и (

(

D1 )

D2 ) . Область

D1 ) определяется неравенствами:

−1 ≤ y ≤ 0 ,

−

1− y2 ≤ x ≤

1− y2 , а область (

) – неравенствами 0 ≤ y ≤1,

D

2

− 1− y ≤ x ≤

1− y . Следовательно, будем иметь

0

x= 1−y2

1

x= 1−y

I = ∫dy

∫ f ( x, y) dx + ∫dy

∫ f (x, y) dx .

−1

x=− 1−y2

0

x=− 1−y

Задача

3.

Переменить

порядок

интегрирования в

повторном интеграле

2a

y= 2ax

I = ∫dx

∫ f (x, y) dy ( a > 0 ).

0

y=

2ax−x2

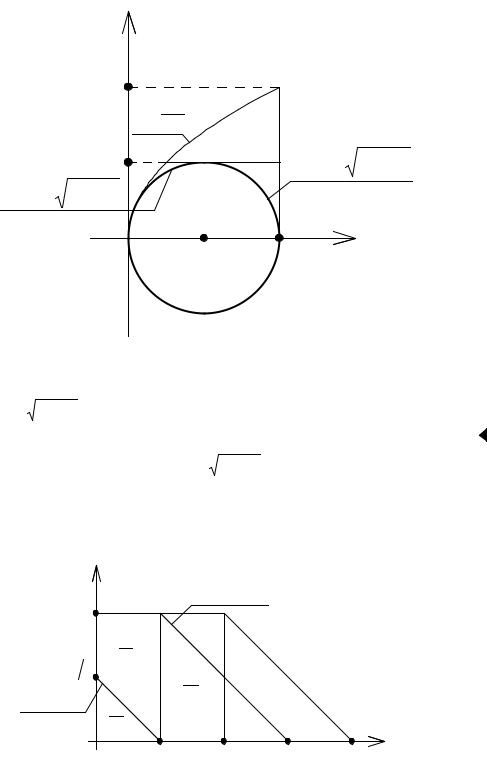
Область интегрирования (

) определяется совместными неравенствами:

D

0 ≤ x ≤ 2a ;

2ax − x2 ≤ y ≤

.

Изобразим

область

(

) на рисунке. Из

2ax

D

рис. 2.15 видим, что если внешнее интегрирование производить по y , то об-

ласть (

) следует разбить линией:

y = a на три области: (

D

D1 ) , (D2 ) , (D3 ) .

Область (

D1 ) определяется неравенствами:

y

2

0 ≤ y ≤ a,

≤ x ≤ a −

a

2

− y

2

;

2a

область (

D2 ) – неравенствами:

0 ≤ y ≤ a, a + a2 − y2 ≤ x ≤ 2a ;

область (

D3 ) – неравенствами

y2

a ≤ y ≤ 2a,

≤ x ≤ 2a .

2a

49

	y
	2a	y2	x =2a
	x =
		2a
	a		x =a +	a2−y2
x =a −	a2−y2			x
		a	2a
	Рис. 2.15. К задаче 3

Следовательно, будем иметь:

a	x=a− a2 −y2			a	x=2a	2a	x=2a
I = ∫dy	∫ f (x, y) dx + ∫dy				∫ f ( x, y) dx + ∫dy ∫ f ( x, y) dx .
0	x=	y2		0	x=a+ a2 −y2	a	x=	y2
		2a						2a

Задача 4. Вычислить I = ∫∫		cos( x + y)								0	≤ x ≤ π,
								dxdy , где (D ) =			≤ y ≤ π.
										0
( D )
y						3π −x
			y =
π						2
			(	D	4)

	π	π 2	(D2)
y =				(D3)
	2	−x	(D1)			x
			π	π	3π	2π
			2		2
			Рис. 2.16. К задаче 4

Отметим прежде всего, что cos(x

				≤ x ≤	π	; 0	≤ y ≤	π
(D ) = 0					2			2	− x и
1

cos(x + y) ≤ 0 в областях:

	+ y) ≥ 0 в областях:
				π		3π
	(D ) =				≤ x ≤ π;
						2	− x ≤ y ≤ π .
	4			2

50