Госы 5к Надя / лекции_3 / int_ zaw_ot_ par / Математический анализ - Интегралы - Аксёнов - 2000 - 145

( K2 ) (см. рис. 3.25), то условие непрерывности в области ( D2 ) , ограниченной контурами ( K1 ) и ( K2 ) , будет иметь место, но нарушится односвязность.

Дополнение.	Пусть	выполнены	все условия теоремы,	а	значит,
∫P( x, y) dx + Q( x, y) dy		по любому незамкнутому пути (AB ,		целиком ле-
(AB
жащему в ( D) , не зависит от формы пути, а зависит только от концов пути.
Пусть функция u( x, y) определена в ( D) и такая, что
	P( x, y) dx +Q( x, y) dy = du( x, y)
(т. е. выражение	P dx +Q dy является		полным дифференциалом		функции
u( x, y)). Тогда

∫P( x, y) dx + Q( x, y) dy = u( xB , yB ) − u( xA, yA )

(AB

(здесь xA, yA – координаты точки A , а xB , yB – координаты точки B). По условию P( x, y) dx +Q( x, y) dy = du( x, y) . Это значит, что

P( x, y) =

∂u( x, y)

;

Q( x, y) =

∂u( x, y)

.

∂x

∂y

Следовательно,

∂u( x, y)

∂u( x, y)

I = ∫P( x, y) dx + Q( x, y) dy =

∫

dx +

dy .

∂x

∂y

(AB

(AB

Для вычисления интеграла I введем параметрические уравнения (AB . Пусть

x = ϕ(t),

t [ p,q], причем значению t = p

отвечает точка A , а

они такие:

y = ψ(t),

значению t = q отвечает точка B. Будем иметь тогда

q

∂u(ϕ(t), ψ(t))

∂u(ϕ(t), ψ(t))

ϕ′(t)

+

∂x

∂y

I = ∫

ψ′(t) dt .

p

Заметив это, рассмотрим функцию f (t) = u(ϕ(t), ψ(t)). По правилу дифферен-

цирования сложной функции, имеем

f ′(t) =

∂u(ϕ(t), ψ(t))

ϕ′(t) +

∂u(ϕ(t), ψ(t))

ψ′(t).

∂y

∂x

Следовательно, предыдущее выражение для I принимает вид

q

I = ∫ f ′(t) dt = f (q) − f ( p) .

p

81

Но f (q) = u(ϕ(q), ψ(q))= u( xB , yB ) ; f ( p) = u(ϕ( p), ψ( p))= u( xA, yA ) (у нас ϕ( p) = xA , ψ( p) = yA , ϕ(q) = xB , ψ(q) = yB ). Поэтому

I = u( xB , yB ) −u( xA, yA ) .

Таким образом, для вычисления интеграла ∫P dx + Q dy нужно найти

(AB

функцию u( x, y), первообразную для дифференциала P dx +Q dy и составить

разность значений этой первообразной в конце и в начале пути интегрирования. Ясно, что это – аналог формулы Ньютона – Лейбница.

Примеры к §4.

1. Вычислить I = ∫( x − y)(dx − dy) , где (AB – любая кривая, соединяю-
(AB
щая точки A(1, −1) и B(1, 1).
В этом случае P( x, y) = x − y ; Q( x, y) = y − x	∂P =	∂Q	= −1 на всей
	∂y	∂x

плоскости. Следовательно, в любой односвязной области, расположенной в плоскости Oxy , подынтегральное выражение является полным дифференциа-

лом некоторой функции u( x, y). Так как

( x − y)(dx − dy) = ( x − y) d( x − y) = 12 d(( x − y)2 ),

то такой функцией u( x, y) будет: u( x, y) = 1 ( x − y)2 . Поэтому
		2
I =	( x − y)2			(1, 1)	22	= −2 .
	2			= 0 −	2
				(1, −1)
							где (AB
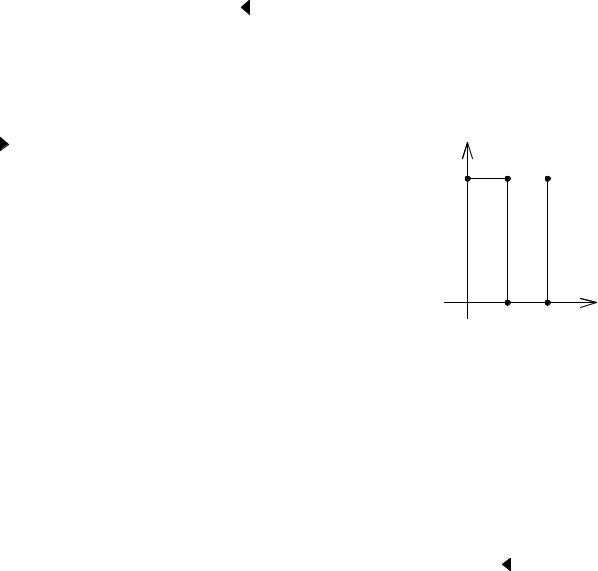
2. Вычислить I = ∫( x4 + 4xy3 ) dx +(6x2 y2 −5 y4 ) dy ,									– любая
(AB
кривая, соединяющая точки A(−2, −1) и B(3, 0).
Здесь P( x, y) = x4 + 4xy3 ;		Q( x, y) = 6x			2 y2 −5 y4		∂P =	∂Q	=12xy2
							∂y	∂x

	y
−2	B x
	3

A

−1

C

на всей плоскости Oxy . Следовательно, I не за-

висит от формы пути интегрирования, соединяющего точки A и B. А раз так, то возьмем, например, в качестве пути (AB ломаную AC UCB

(см. рис. 3.26). Тогда

Рис. 3.26. К примеру 2	I = ∫	= ∫	+ ∫ (= I1 + I2 ) .
Имеем:	(AB	(AC	(CB

82

(AC = −2 ≤ x ≤ 3

dy = 0 .

Поэтому

y = −1

3

3

4

x5

2

I1 = ∫

= ∫( x

−4x) dx + 0 =

−

2x

= 45 .

5

(AC

−

−2

Имеем:

2

x = 3

(CB =

dx = 0 .

Поэтому

−1 ≤ y ≤ 0

0

−01 =17 .

I2

=

∫

= ∫(54 y2 −5 y4 ) dy = (18 y3 − y5 )

(CB

−1

Следовательно, I = 45 +17 = 62.

∫

y2

y

y

y

y

(AB –

3. Вычислить

I =

1 −

cos

dx

+ sin

+

cos

dy , где

2

(AB

x

x

x

x

x

любая кривая, соединяющая точки A(1, π)

и

B(2, π)

и не пересекающая ось

Oy .

y

Здесь

B

P( x, y) =1−

y

2

cos

y

;

Q( x, y) = sin

y

+

y

cos

y

;

π

A

x2

x

x

y

y2

y

x

x

∂P =

∂Q

= − 2 y cos

+

sin

, x ≠ 0 .

∂x

x

x

∂y

x2

x3

Видим, что P( x, y) , Q( x, y) ,

∂P

∂Q

x

∂y

, ∂x

определены и не-

1

2

прерывны на всей плоскости Oxy , кроме точек, лежащих

Рис. 3.27.

∂P =

∂Q

на оси Oy , и что

для x ≠ 0 . Следовательно,

I

К примеру 3

∂y

∂x

не зависит от формы пути (AB . Требуется только, чтобы (AB не пересекала ось Oy . А раз так, то возьмем, например, в качестве (AB прямолинейный от-

резок, соединяющий точки A и B (см. рис. 3.27). Так как

			(AB = 1 ≤ x ≤ 2,				dy = 0 ,
то будем иметь					y = π
2		π2			π			π			x=2
I = ∫	1 −		2	cos	dx + 0 =						=1 + π.
						x + πsin
1		x			x			x			x=1

83

§5. Площадь плоской фигуры в криволинейных координатах

1°. Вычисление площади плоской фигуры при помощи криволинейного

интеграла второго рода.

Пусть ( K ) – простой, замкнутый самонепересекающийся контур, ограничивающий область ( D) .

1) Пусть область ( D) такая, что прямыми, параллельными оси Oy , она может быть разложена на конечное число областей типа I. Рассмотрим криволи-

нейный интеграл ∫y dx (это – частный случай интеграла							∫P dx +Q dy , когда
	( K )					( K )
P ≡ y ,	а Q ≡ 0 ). Преобразуя ∫y dx по					формуле	Грина, получим
					( K )
∫y dx = − ∫∫dxdy = −F
		D
( K )	( D )
			F		= − ∫y dx .		(1)
				D
					( K )

2)Пусть теперь область ( D) такая, что прямыми, параллельными оси Ox ,

ееможно разложить на конечное число областей типа II. Рассмотрим криволи-

нейный интеграл		∫x dy (это – частный случай интеграла							∫P dx +Q dy , когда
		( K )							( K )
P ≡ 0 ,	Q ≡ x ).	Преобразуя				∫x dy		по формуле	Грина, получим:
					( K )
∫x dy = ∫∫dxdy = F
			D
( K )	( D )
					F		= ∫x dy .		(2)
						D
							( K )
3) Пусть, наконец,				область	( D) такая,			что прямыми,	параллельными оси

Oy , она может быть разложена на конечное число областей типа I, а прямыми,

параллельными оси Ox , – на конечное число областей типа II. Тогда будут верны одновременно формулы (1) и (2). Сложив соответствующие части этих формул, получим

2F		= ∫x dy − y dx	F		= 12 ∫x dy − y dx .	(3)
	D			D
		( K )			( K )

84

( D ).

(∆), и пусть ее

2°. Формула для площади плоской фигуры в криволинейных координа-

тах.

Пусть в плоскостях Oxy и Oξη расположены области ( D) и (∆) с простыми контурами ( KD ) и ( K∆ ) . Если дано правило, которое каждой точке (ξ, η) из (∆) сопоставляет одну и только одну точку ( x, y) из ( D ), причем каждая точка ( x, y) из ( D ) оказывается сопоставленной одной и только одной точке из (∆), то говорят, что между точками областей ( D ) и (∆) установлено

взаимно-однозначное соответствие.

y

η

( D)

(∆)

(KD)

x

(K∆)

ξ

O

а)

O

б)

Рис. 3.28. К выводу формулы для площади в криволинейных координатах

Если (ξ, η) и ( x, y) есть взаимно-соответствующие точки, то

x = x(ξ, η),

(4)

y = y(ξ, η).

Уравнения (4) есть уравнения преобразования (

) в (

). В силу взаимной од-

∆

D

нозначности соответствия между точками областей (

) и (

), система (4) од-

D

∆

нозначно разрешима относительно ξ и η. Поэтому

ξ = ξ( x, y),

(5)

η= η( x, y).

Впредь функции x(ξ, η) ,

y(ξ, η)

будем считать непрерывными в (

), а

∆

функции ξ( x, y), η( x, y) – непрерывными в ( D ). Покажем, что тогда непрерывные кривые, лежащие, например, в (∆), преобразуются в непрерывные кривые, лежащие в

В самом деле, пусть (λ) – непрерывная кривая, лежащая в

ξ = α(t),	где α(t) , β(t) – функции, опре-
параметрические уравнения такие:
η= β(t),

деленные и непрерывные в промежутке [ p, q]. Тогда точки, соответствующие точкам кривой (λ) , имеют координаты:

85

x = x(α(t),β(t)),

y = y(α(t),β(t)). (6)

Так как правые части в уравнениях (6) есть функции непрерывные в промежутке [ p, q], как суперпозиции непрерывных функций, то заключаем, что непре-

рывная кривая (λ) преобразуется в непрерывную же кривую (l), лежащую в области ( D ).

Задача. Зная область (∆) и формулы преобразования области (∆) в область

		x = x(ξ, η),	найти площадь F
( D ):					области ( D ).
				D
		y = y(ξ, η),

Решать эту задачу будем при следующих предположениях.

1)Обе области (∆) и ( D ) прямыми, параллельными координатным осям, разлагаются на конечное число областей как типа I, так и типа II.

2)Контуру ( K∆ ) соответствует контур ( KD ) , причем положительному об-

ходу ( K∆ ) соответствует определенный (положительный или отрицательный)

обход ( KD ) .

3) Функции x(ξ, η) и y(ξ, η) имеют в (∆) непрерывные частные производные первого порядка xξ′, xη′ , yξ′, yη′ , а одна из этих функций имеет в (∆) непрерывные смешанные производные второго порядка. Пусть, например, в (∆)

существуют и непрерывны y′′

и y′′

( y′′

= y′′

в (

)).

∆

ξη

ηξ

ηξ

ξη

4) Определитель J(ξ, η) =

xξ′ xη′

сохраняет знак ( J(ξ, η) –

всюду в (∆)

y′

y′

ξ

η

определитель Якоби, или якобиан).

Решение. Мы знаем, что F

=

∫x dy . Выразим этот криволинейный инте-

D

( KD )

грал через обыкновенный определенный интеграл. Пусть параметрические

ξ = α(t),

t [ p, q], где α(t) , β(t) – функции,

уравнения контура ( K∆ ) такие:

η= β(t),

определенные на [ p, q] и имеющие там непрерывные производные α′(t), β′(t) .
Тогда параметрические уравнения контура ( KD ) будут такими:
x = x(α(t),β(t)),	t [ p,q].
y = y(α(t),β(t)),
Пусть для определенности изменению t от	p до q соответствует положитель-

ный обход контура ( KD ) . Тогда

86

q

FD = ∫x(α(t),β(t)) [yξ′(α(t),β(t))

α′(t) + yη′ (α(t),β(t)) β′(t)]dt . (7)

p

Рассмотрим теперь следующий криволинейный интеграл второго рода по контуру ( K∆ ) :

I = ∫x(ξ, η) [yξ′(ξ, η) dξ + yη′ (ξ, η) dη].

(8)

( K∆ )

Чтобы выразить I обыкновенным определенным интегралом, нужно использовать параметрические уравнения контура ( K∆ ) . Сделав это, мы придем в точности к интегралу, стоящему в правой части (7), если только положительный обход контура ( KD ) соответствует положительному обходу контура ( K∆ ) . Если же положительный обход контура ( KD ) соответствует отрицательному обходу контура ( K∆ ) , то мы получим интеграл стоящий в правой части (7), взятый со знаком «минус». Таким образом,

F

= ±I .

(9)

D

Преобразуем интеграл I (см. (8)) по формуле Грина

∫

P(ξ, η) dξ +Q(ξ, η) dη=

∫∫

∂Q

−

∂P

∂ξ

∂η

dξdη.

( K∆ )

( ∆)

У нас в I :

P = x(ξ, η) yξ′(ξ, η), Q = x(ξ, η) yη′ (ξ, η). Значит,

∂Q

= x′

y′

+ x y′′

∂Q −

∂P = x′

∂ξ

ξ

η

ηξ

y′

− x′

y′ = J(ξ, η) .

∂P

= x′

y′

+ x y′′

∂ξ

∂η

ξ

η

η

ξ

∂η

η

ξ

ξη

Поэтому

I = ∫∫( xξ′ yη′ − xη′ yξ′ ) dξdη= ∫∫J(ξ, η) dξdη.

( ∆)

(∆)

А, следовательно,

FD = ±∫∫J(ξ, η) dξdη.

( ∆)

У нас по условию J(ξ, η) всюду в (∆) сохраняет знак. Поэтому, принимая во

внимание, что F		> 0 , можем написать
	D
		F		= ∫∫		J(ξ, η)		dξdη.	(10)
			D
				( ∆)
Из рассуждений, проведенных выше, следует, что									J(ξ, η) > 0 тогда, когда

положительный обход контура ( KD ) соответствует положительному обходу

87

контура ( K∆ ) и что J(ξ, η) < 0 тогда, когда положительный обход контура ( KD ) соответствует отрицательному обходу контура ( K∆ ) .

К двойному интегралу, стоящему в правой части (10), применим частный

случай теоремы о среднем. Получим.

F

=

J(

, η)

F

, где (

ξ

, η) (

) .

(11)

ξ

∆

F

D

∆

Из (11) находим

D

=

J(ξ, η)

. Станем сжимать область

(∆)

по всем направ-

F

∆

лениям в некоторую точку (ξ, η) (тогда (ξ, η) → (ξ, η) ). В силу непрерывности отображения область ( D) будет при этом сжиматься в точку ( x, y), которая соответствует точке (ξ, η) . Следовательно,

J (ξ, η) = lim FD .

F∆→0 F∆

Таким образом, модуль якобиана есть коэффициент искажения площадей при переходе из плоскости Oξη в плоскость Oxy .

Замечание. Формула (10) остается верной и в том случае, когда взаимнооднозначное соответствие между точками областей ( D ) и (∆) нарушается на множестве точек, лежащих на конечном числе простых кривых. При этом предполагается, что якобиан J(ξ, η) остается ограниченным всюду в (∆).

§6. Замена переменных в двойном интеграле

Пусть между точками областей ( D ) и (∆) установлено взаимно-

x = x(ξ, η),

однозначное соответствие посредством формул y = y(ξ, η). Считаем, что вы-

полняются все условия, указанные при выводе формулы для площади плоской фигуры в криволинейных координатах.

Пусть в области ( D ) задана непрерывная функция f ( x, y). Мы знаем, что тогда существует двойной интеграл I = ∫∫ f ( x, y) dxdy . Требуется выразить I

( D )

через некоторый двойной интеграл по области (∆).

Составим интегральную сумму Римана для двойного интеграла I . Для этого произвольной сетью простых кривых нужно разбить область ( D ) на части ( D1 ) , ( D2 ) , K , ( Dn ); в каждой части ( Dk ) взять произвольную точку

n

( xk , yk ) , и тогда σ = ∑ f ( xk , yk ) FDk .

k=1

88

Заметим, что, проводя в ( D ) сеть простых кривых, мы, в силу однозначности отображения, будем проводить также сеть простых кривых в области (∆), так что (∆) разобьется на части (∆1 ), (∆2 ), K , (∆n ) .

По формуле для площади плоской фигуры в криволинейных координатах, имеем

FDk = ∫∫ J(ξ, η) dξdη.

( ∆k )

Применяя к двойному интегралу, стоящему в правой части, частный случай теоремы о среднем, получим

F

=

J(

k , ηk )

F

, где точка

(

k , ηk ) (

k ).

ξ

ξ

∆

D

∆

k

k

А тогда

n

σ = ∑ f ( xk , yk )

J(

k , ηk )

F

k .

ξ

∆

k=1

I существует. Следовательно,

Было отмечено, что у нас двойной интеграл

lim σ = I при любом выборе точек ( xk , yk ) в ( Dk ). В частности, в каче-

λ→0

стве точек ( xk , yk ) можно взять точки, соответствующие точкам (ξk , ηk ) , т. е.

положить xk = x(ξk , ηk ), yk = y(ξk , ηk ) . При таком выборе точек ( xk , yk ) будем иметь:

n

σ = ∑ f (x(ξk , ηk ), y(ξk , ηk )) J(ξk , ηk ) F∆k .

k=1

Сумма, стоящая здесь в правой части, есть сумма Римана для двойного интеграла

I* = ∫∫ f (x(ξ, η), y(ξ, η)) J(ξ, η) dξdη,

( ∆)

причем I* существует, ибо подынтегральная функция в нем есть функция непрерывная в (∆).

Отметим, что, измельчая дробление в ( D ), мы тем самым будем измельчать дробление и в (∆), ибо функции, осуществляющие взаимно-однозначное отображение областей ( D ) и (∆) друг на друга, есть непрерывные функции. Но

тогда σ → I* при λ → 0 . А так как σ → I при λ → 0 , то получаем I = I* , т. е.
∫∫ f ( x, y) dxdy = ∫∫ f (x(ξ, η), y(ξ, η))				J(ξ, η)		dξdη.	(1)
( D )	( ∆)
x = r cosϕ,		Тогда
Частный случай. Пусть
y = r sin ϕ.

89

∫∫ f ( x, y) dxdy = ∫∫ f (r cos ϕ, r sin ϕ)r drdϕ.

( D ) ( ∆)

Замечание. Формула (1) остается верной и тогда, когда взаимнооднозначное соответствие между точками областей ( D ) и (∆) нарушается на множестве точек, лежащих на конечном числе простых кривых. При этом предполагается, что якобиан J (ξ, η) остается ограниченным всюду в (∆).

§7. Примеры к главе 3

+∞

Пример 1 (интеграл Эйлера). Вычислить I = ∫e−x2 dx (попутно будет до-

0

y

казана сходимость этого несобственного интеграла).

Введем в рассмотрение функцию

f ( x, y) = e−x2 −y2

и области (

) ,

(

) , (

) , где:

D

D

D

1

2

3

(

) – четверть круга: x2 + y2 ≤ R2 , лежащая в

D

1

x

первой четверти;

0 ≤ x

≤ R,

R R 2

( D2 ) – квадрат:

≤ R;

0 ≤ y

Рис. 3.29.

(

D3 ) – четверть круга: x2 + y2 ≤ 2R2 , лежащая в

К вычислению

первой четверти.

интеграла Эйлера

Ясно, что ( D1 ) ( D2 ) ( D3 ) . Отсюда и из того,

что f ( x, y) > 0 следует:

∫∫e−x2 −y2 dxdy ≤ ∫∫e−x2 −y2 dxdy ≤ ∫∫e−x2 −y2 dxdy .

(2)

( D )

( D )

( D )

1442443

12442443

13442443

=I1

=I2

=I3

Выразим двойной интеграл I2 через повторный.

R

R

R

R

I2 = ∫∫e−x2 −y2 dxdy = ∫dx∫e−x2

− y2 dy = ∫e−x2 dx∫e− y2 dy =

( D2 )

0

0

0

2

0

R

2

R

−x

2

R

−x

2

−y

∫e

∫e

=

∫e

dy

dx

=

dx .

0

0

0

Вычисление двойных интегралов I1, I3 будем производить, переходя к полярным координатам. Будем иметь

90