§24. Непрерывность обратной функции

Теорема. Пусть f(x) строго монотонна (т.е. или возрастает, или убывает) и непрерывна на . Тогда существует обратная функцияопределенная, строго монотонная и непрерывная наE(f).

Доказательство.

Пусть функция y=f(x) непрерывна и монотонна на , ее множество значений промежуток с концами. По теореме о существовании обратной функции существует обратная функция, определенная и строго монотонная наE(f). Причем, если f(x) возрастает (убывает) то и обратная функция возрастает (убывает).

Докажем, чтонепрерывна наE(f). Доказательство проведем для возрастающей функции .

Возьмем

.

Докажем, что непрерывна в точкеy₀. По определению надо доказать, что выполнено .

Возьмем , рассмотрим . Так каки функция возрастает, то.

Обозначим ,

,

положим , т.е.и.

Тогда

. (1)

Возьмем , удовлетворяющее неравенству,(2)

Тогда из (1) и (2) следует, что . (3)

Так как возрастает, то из (3) следует, т.е..

Получили, что выполнено . Значит,непрерывна в точкеy₀. Т.к. y₀ - произвольная точка из E(f), то непрерывна наE(f).

§25. Непрерывность элементарных функций

1. Определение элементарной функции.

Основные элементарные функции:

- степенная,

, - показательная,

- логарифмическая,

- тригонометрические,

- обратные тригонометрические.

Определение. Элементарной называется функция, которая получается из основных элементарных функций путем конечного числа композиций и четырех арифметических операций.

Теорема. Всякая элементарная функция непрерывна во всех точках своей области определения.

Доказательство следует из утверждений:

1. основные элементарные функции непрерывны в своей области определения;

2. арифметические действия над непрерывными функциями дают непрерывные функции;

3. композиция непрерывных функций есть непрерывная функция;

4. функция, обратная непрерывной, является непрерывной.

Пример. 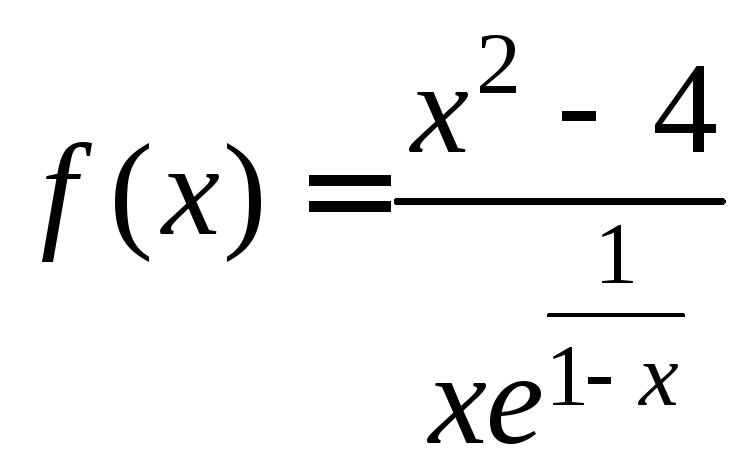 - элементарная функция.

2. Степенная функция.

Рассмотрим степенную функцию у=х^, где . Она имеет то или иное конкретное содержание в зависимости от значений (см. Бохан К. А. т.1 с.55 – самостоятельно). В любом случае она определена при х>0.

Из определения логарифма и свойств показательной функции следует

.

Тогда из монотонности показательной и логарифмической функции следует, что степенная функция тоже монотонна: возрастает при >0 и убывает при . <0. Покажем это. Степенная функция является композицией функций y=a^t и t=log_ax.

1) Пусть >0.

а) При a>1 функции y=a^t и t=log_ax возрастают. Следовательно, степенная функция возрастает как композиция двух возрастающих функций.

б) При 0<a<1 функции y=a^t и t=log_ax убывают. Следовательно, степенная функция возрастает как композиция двух убывающих функций.

2) Пусть <0.

а) При a>1функция y=a^t возрастает, а t=log_ax - убывает. Следовательно, степенная функция убывает как композиция возрастающей и убывающей функции.

б) При 0<a<1 функция y=a^t убывает, а функция t=log_ax возрастает. Следовательно, степенная функция убывает как композиция убывающей и возрастающей функции.

При =0 степенная функция обращается в постоянную: х⁰1.

Из непрерывности показательной и логарифмической функции и теоремы о непрерывности сложной функции следует, что степенная функция непрерывна на своей области определения. Действительно, имеем

.
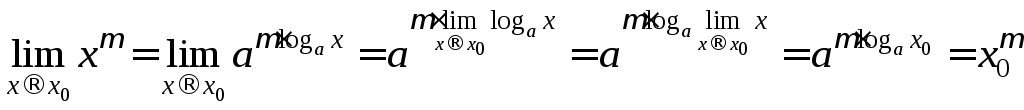