§4. Частные производные и дифференцируемость функции нескольких переменных
Лк (2ч)
Понятие частных производных
Рассмотрим вначале
случай функции двух переменных. Пусть
функция z=f(x,y)
определена на открытом множестве
,
(х0,у0)
– внутренняя точка множества G.
Определение. Если существует конечный предел
,
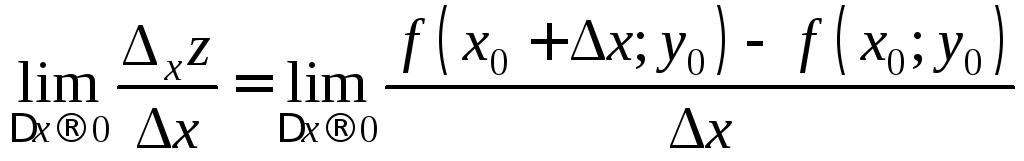то он называется
частной
производной функции
z=f(x,y)
по переменной
х
в точке (х0,у0)
и обозначается
,
,
,
.
Если существует конечный предел
,
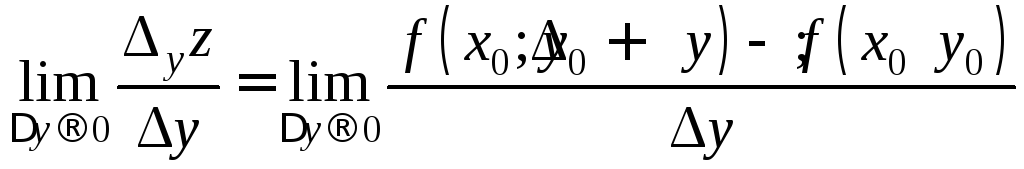то он называется
частной
производной функции
z=f(x,y)
по переменной
у
в точке (х0,у0)
и обозначается
,
,
,
.
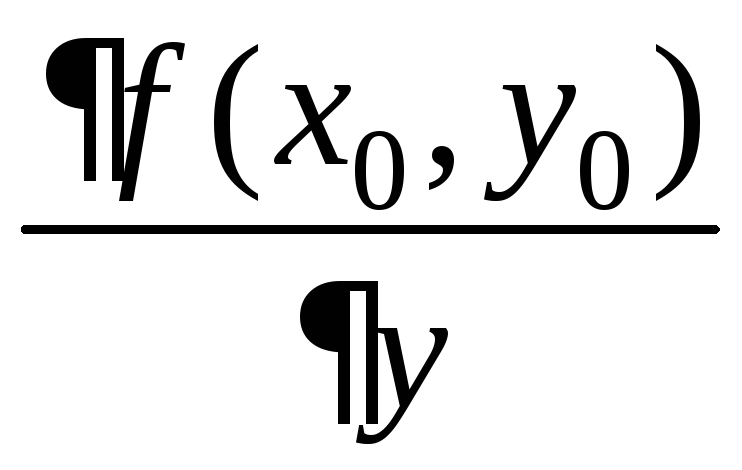Итак, 
=
,
=
.
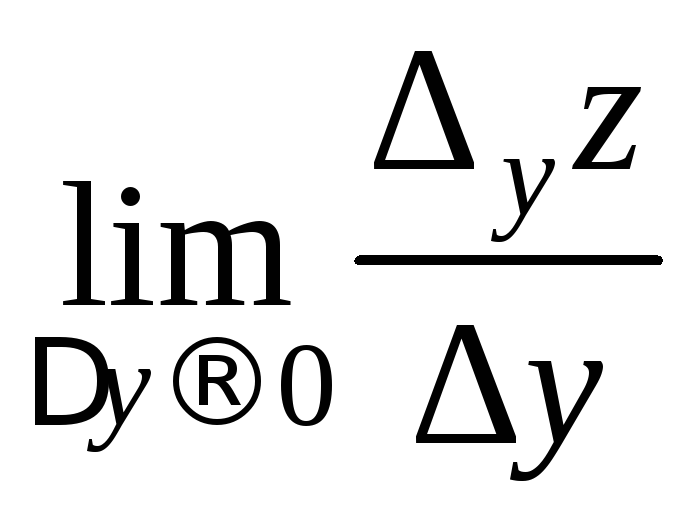Из определения
следует, что частная производная функции
z=f(x,y)
по переменной х
в точке (х0,у0)
является обычной производной функции
одной переменной f(х,у0)
в точке х0.
Если функция z=f(x,y)
имеет частную производную
в каждой точке (х,у)G,
то говорят, что частная производная
существует на G.
В этом случае каждой точке (х,у)G
соответствует число
.
Этим на множествеG
определяются две функции , которые
обозначаются
и
,
и называются частными производными
функцииf
на множестве G.
Т.к. частная производная
функцииf
определяется как обычная производная
функции одной переменной х
(или у),
получаемой из f
фиксированием
другой переменной у
(или х),
то правила дифференцирования функций
одной переменной применимы для нахождения
частных производных функций нескольких
переменных.
Пример 1.
Найти частные производные функции
.
.
,
.
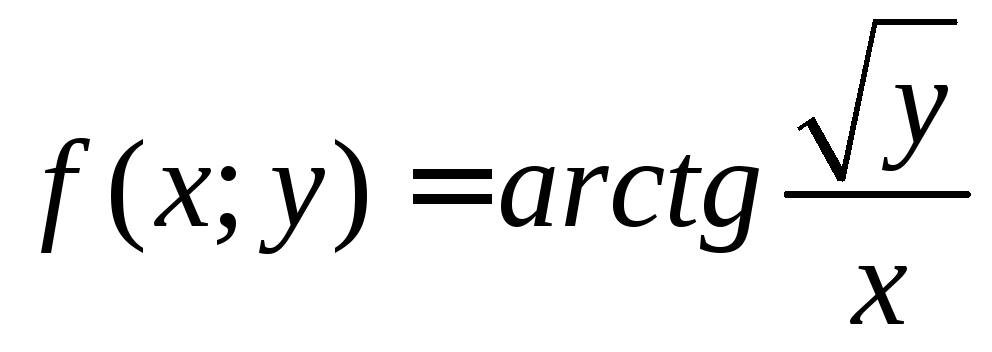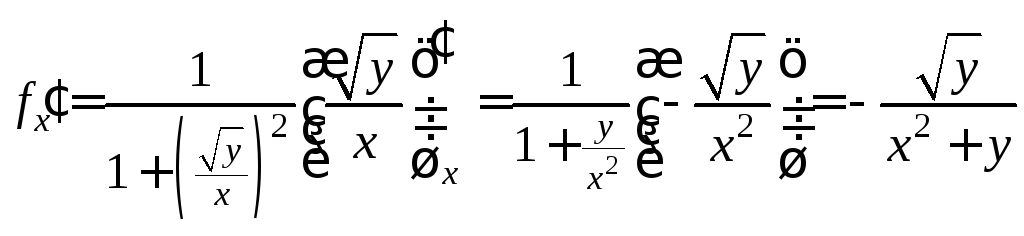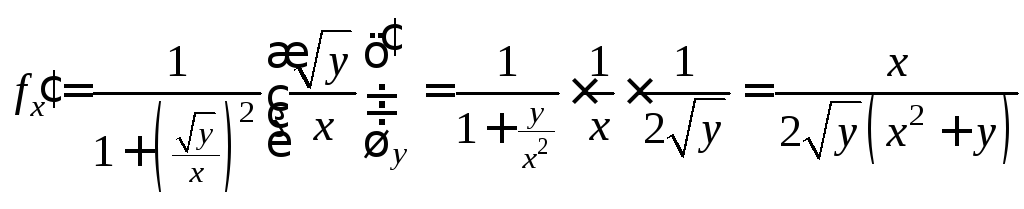Аналогично определяются частные производные функции трех и большего числа переменных.
Пусть функция
u=f(x1,x2,…xn)
определена на открытом множестве
,
- внутренняя точка множестваG.
Определение. Если существует конечный предел
,
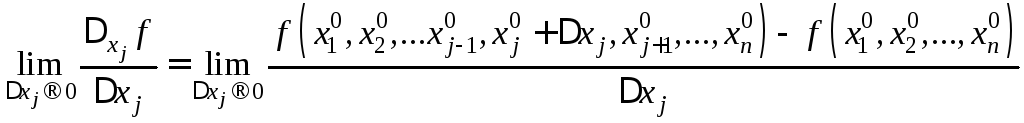
то он называется
частной
производной функции
u=f(x1,x2,…xn)
по переменной
xj
в точке
и обозначается
,
,
,
.
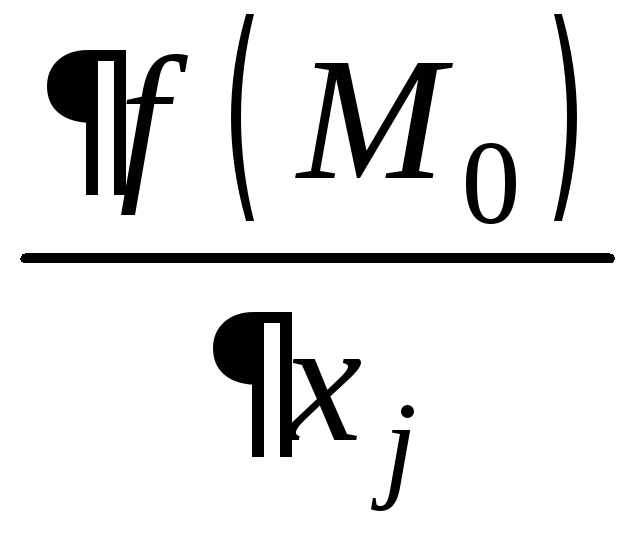Геометрический смысл частных производных
Пусть
функцияz=f(x,y)
определена на множестве
.
Рассмотрим поверхностьz=f(x,y),
являющуюся графиком этой функции. Пусть
точка M0(x0,y0,z0)
принадлежит поверхности. Проведем через
точку M0
плоскость x=x0,
параллельную плоскости yOz.
Кривая z=f(x0,y)
является линией пересечения поверхности
и плоскости. Частная производная данной
функции по переменной у
совпадает с производной функции f(x0,y)
в точке у=у0:
.
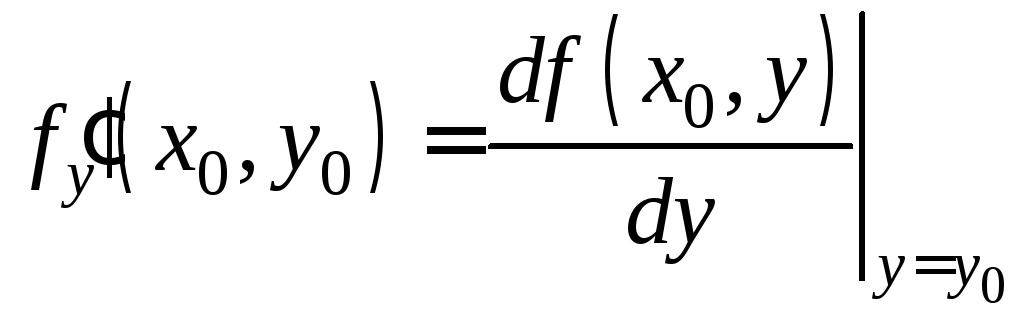Следовательно,
равна угловому коэффициенту касательной
к кривойz=f(x0,y)
в точке M0(x0,y0,z0).
,
где
- угол между касательной и положительным
направлением оси Оу.
2. Дифференцируемость и дифференциал функции нескольких переменных
Пусть функция
z=f(x,y)
определена на множестве
,
(х0,у0)
– внутренняя точка множества G.
Придадим значениям х0
и у0
приращения х
и у,
одновременно не равные нулю, так, что
точка (х0+х,у0+у)G.
Тогда полное приращение функции
z=f(х0+х,у0+у)-f(х0,у0).
Определение.
Пусть функция z=f(x,y)
определена на множестве
.
Функцияf(x,y)
называется дифференцируемой
в точке
(х0,у0)G,
если ее полное приращение в этой точке
можно представить в виде
z=Ах+Ву+х+у, (1)
где А, В - постоянные, =(x,y), =(x,y)- бесконечно малые функции.
Полное приращение дифференцируемой функции можно записать также в виде:
z=Ах+Ву+, (2)
где
,
.
Покажем, что (1)эквивалентно (2).
1) (1)(2). Т. к. первые два слагаемых одинаковые, то надо показать, что х+у можно представить в виде (с выполнением соответствующих условий).
,
где
.
, (*)
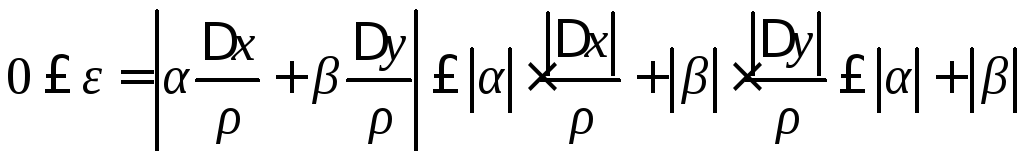т.к.
.
Пусть
,
тогдаx0,
y0.
Значит, по условию,
0,
0.
Следовательно, в силу неравенства (*),
0.
Итак, 0
при 0.
2) (2)(1).
,
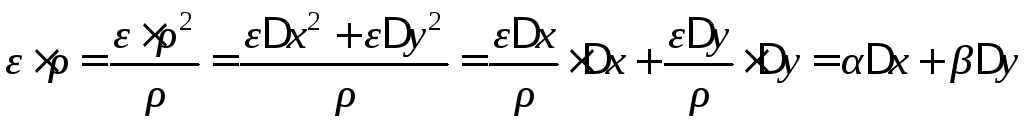где
.
. (**)
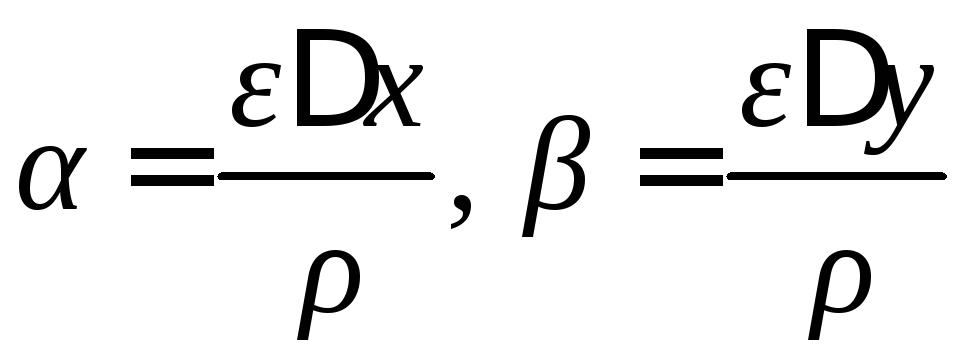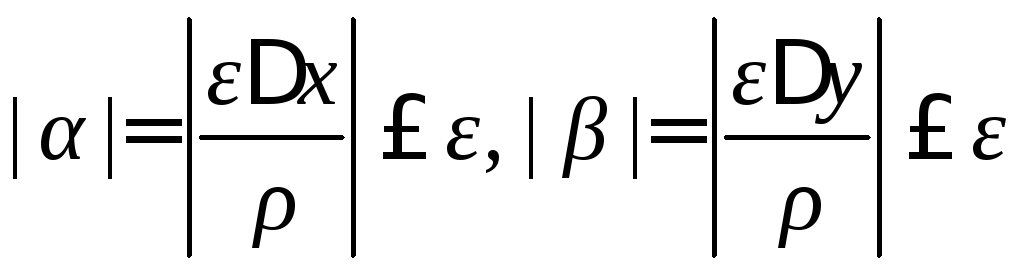Пусть x0, y0. Тогда 0. Отсюда, по условию, 0. А, значит, в силу неравенств (**), 0, 0.
Итак, условия (1) и (2) эквивалентны.
Замечание.
Т.к.
,
то=()
при 0,
и (2) можно записать в виде
z=Ах+Ву+(). (3)
Определение. Пусть функция z=f(x,y) дифференцируема в точке (х0,у0). Дифференциалом функции f в точке (х0,у0). Называется линейная относительно x и y часть полного приращения функции в точке (х0,у0).
Обозначается dz, df(х0,у0).
dz=Ах+Ву. (4)
Т.о., z=dz+х+у или z=dz+(). (5)
Т.к. z-dz=(), то z и dz одного порядка малости при 0. Из (5) также следует, что dz0 – главная часть полного приращения функции при 0. Т.о., дифференциал обладает двумя свойствами:
1) является линейной частью приращения функции;
2) если dz0, то он является главной частью полного приращения при 0.
Из второго свойства следует применение дифференциала к приближенным вычислениям:
f(х0,у0)df(х0,у0) при 0,
f(х0+х,у0+у)=f(х,у)f(х0,у0)+df(х0,у0).
Теорема 1 (непрерывность дифференцируемой функции). Если функция z=f(x,y) дифференцируема в точке (х0,у0), то она непрерывна в этой точке.
Доказательство.
Пусть функция
z=f(x,y)
дифференцируема в точке (х0,у0).
Тогда ее полное приращение может быть
представлено в виде (1)
z=Ах+Ву+х+у,
где А,
В
- постоянные,
.
Пусть x0,
y0.
Тогда 0,
0,
и, значит, f(х0,у0)0.
Т.е. бесконечно малым приращениям
аргументов в точке (х0,у0)
соответствует бесконечно малое полное
приращение функции. Следовательно, по
определению, функция z=f(x,y)
непрерывна в точке (х0,у0).
Лк (2ч)
Теорема
2 (необходимое
условие дифференцируемости). Если
функция z=f(x,y)
дифференцируема в точке (х0,у0),
то в этой точке существуют конечные
частные производные
,
,
и имеет место равенство:
, (6)
т.е. всегда
.
Доказательство.
Т.к. функция
дифференцируема в точке (х0,у0),
то имеет место (1). Пусть х0
получает приращение х0,
а у0
остается неизменным, т.е. у=0.
Тогда
.
Обозначим
,
.
Тогда
.
Разделим обе части
этого равенства на х0:
.
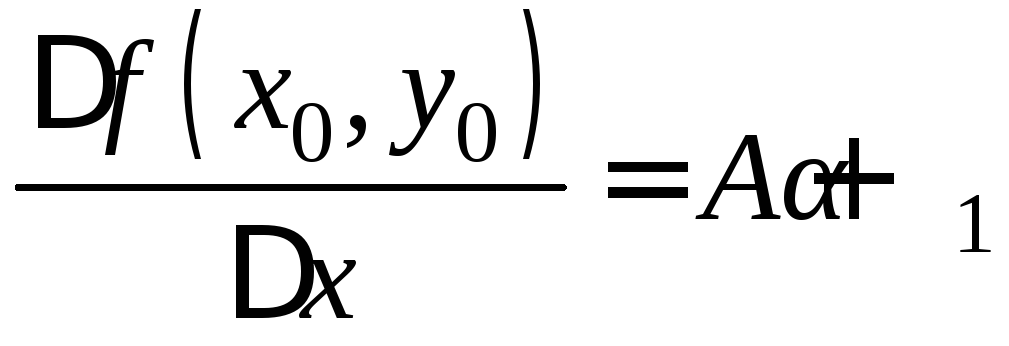Т.к. существует
предел правой части при х0:
,
то существует и предел левой части: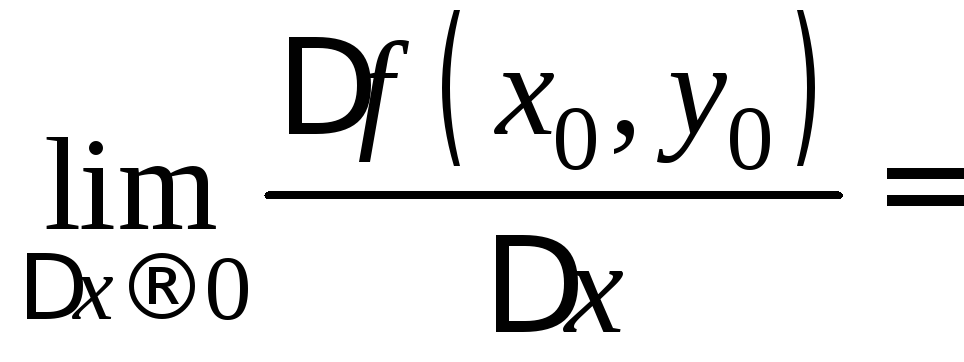
,
и эти пределы равны:
=А.
Аналогично
доказывается, что
=В.
Замечание 1. Теорема, обратная к теореме 1, неверна. Функция, непрерывная в точке (х0,у0), может быть не дифференцируема в ней.
П
ример
3.z=f(x,y)=|x|.
,
функция непрерывна на
.
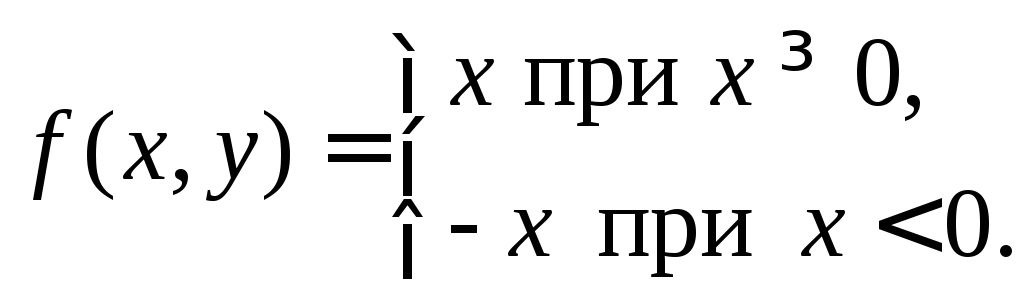
Покажем, что функция дифференцируема везде, кроме точек оси Оу. Зафиксируем у0.
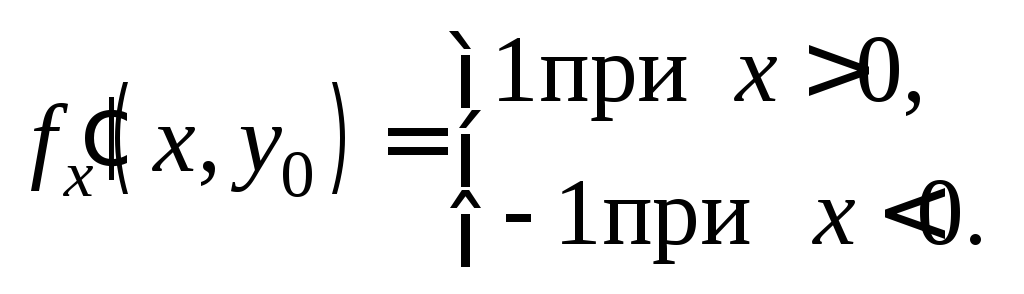
Следовательно,
не существует. Из теоремы 2 следует, что
функция не дифференцируема на оси Оу.
Замечание
2. Теорема,
обратная к теореме 2, не имеет места.
Функция f(x,y),
имеющая частные производные
и
,
может и не быть дифференцируемой в точке
(х0,у0).
Теорема 3
(достаточное
условие дифференцируемости функции
двух переменных).
Пусть функция f(x,y)
в некоторой окрестности точки (х0,у0)
имеет частные производные
и
,
которые непрерывны в точке (х0,у0).
Тогда функция f(x,y)
дифференцируема в точке (х0,у0).
Д
оказательство.
Пусть функция
f(x,y)
и ее частные производные
и
определены в некоторой окрестности
точкиМ0(х0,у0):
.
Придадим х0,
у0
произвольные приращения х
и у,
не равные нулю одновременно и такие,
чтобы
.
Тогда функцияf
получит приращение
,
которое можно представить в виде:
(1)
Первая скобка
является частным приращением по
переменной х
функции f(x,y)
в точке
;
вторая скобка является частным приращением
функцииf(x,y)
по переменной у
в точке (х0,у0).
Т. к. первая скобка является приращением
функции одной переменной 
в
точке х0,
а вторая - приращением функции одной
переменной 
в точке у0,
то к ним можно применить теорему Лагранжа.
В силу условия
функция 
имеет производную
на
,
а функция
имеет
производную на
.Тогда
применяя теорему Лагранжа, получим
=
,(8)
,
.(9)
Подставим (8) и (9) в (7):
,
.
Добавим и вычтем
справа
и
:
. (10)
Обозначим
,
,
,
.
Тогда
.
Если доказать, что
при
,
то функцияf(x,y)
будет дифференцируема в точке (х0,у0)
по определению.
Пусть
.
Так как
,
то
,
,
.
Тогда в силу непрерывности частных
производных в точке (х0,у0)
,
.
Следовательно,
,
.
По определению функцияf(x,y)
дифференцируема в точке (х0,у0).
Лк (2ч)
Дифференцирование сложной функции
Пусть функция
определена
на D,
определены наG=<a,b>.
Если
,
то на G определена функция
- сложная функция одной переменнойt
(1)
Теорема 1 Если
конечные производные
в точке
и непрерывные частные производные
в соответствующей точке
,
то
производная
от сложной функции (1) в точке t и она
может быть найдена по формуле
(2)
Доказательство.
Придавая
точке t приращение
получим
.
Тогдаx
и y
получат соответствующие приращения
и
.
Тогда
получит приращение
в соответствующей точке
.
Так как
в
точке
имеет непрерывные частные производные,
то она дифференцируема в этой точке, и
поэтому ее приращение можно записать
в виде
,
где
.
(3)
Разделим (3) на
:
(4)
Пусть
.
Так как функции
и
дифференцируема
в точке t, то они непрерывны в этой точке.
Тогда если
,
то
,
.
Все это значит,
что правая часть (4) имеет предел ( при
),
равный
.
Тогда существует
предел и левой части (4) при
,
равный
.
Переходя в (4) к
пределу при
,
получим (2).
Теорема 1 справедлива для открытой области D и промежутка G.
Частный случай:
,
то есть
.
Тогда
Пример 1.
,
но
можно было найти непосредственно из
(*).
Эффективность дифференцирования по формуле(2) проявляется в более сложных примерах.
Пример 2.
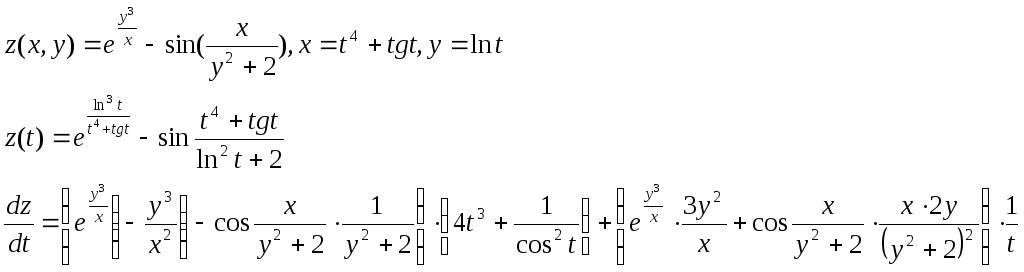
Пусть
определена
наD,
определены
на G
соответствует
.
Тогда на G определена
функция
. (6)
Теорема 2. Если
существуют частные производные
на G и непрерывные частные производные
от сложной функции (6) на G , которые могут
быть вычислены по формулам:
(7)
(8)
Доказательство.
зафиксируем
.
Тогда (6) обращается в сложную функцию
одной переменной, к которой можно
применить теорему (1). На основании этой
теоремы
,
т.е. справедливо (7).
Аналогично, фиксируя
,
получим следующую функцию от одной
переменной
.
Применяя к ней теорему 1, получим формулу
(8).
Пример.
Инвариантная форма дифференциала
I.
определена
на G;
- независимые переменные.
Пусть на D функция f имеет непрерывные частные производные, тогда она дифференцируема и ее дифференциал
,
(1)
где
,
т.е.
- произвольные числа, не зависящие от
.
II. Пусть
,
определены наG;
- независимые переменные.
Пусть
.
Тогда наG
определена сложная функция
.
(2)
Пусть на
соответствующих областях существуют
непрерывные частные производные
на G,
наD.
Тогда
непрерывные частные производные
от сложной функции
:
,(3)
. (4)
Тогда сложная функция (2) дифференцируема, ее дифференциал равен
,
(5)
где
- произвольные числа.
Из (3),(4),(5) следует, что
(6)
- дифференциал
функции, не равный
,
- дифференциал функции, не равный
.
Сравнив (1) и (6)
можно сделать вывод. Дифференциал
функции
имеет одну и ту же форму относительно
:
как для случая, когда
- функции других переменных, так и для
случая, когда
- функции других переменных. Хотя форма
(1) инвариантна, но смысл символов
- не один и тот же.
Если
-
независимые переменные, то
-
не зависят от
(числа).
Если
-
функции, то
-
дифференциалы этих функций.
Итак, так как (1)
инвариантна, то дифференциал функции
всегда
может быть записан в виде (1).
Замечание. Если
-
независимые переменные, то существуют
2 формы записи дифференциала:
Если
-
функции, то
и
Лк (2ч)