§6. Производная по направлению. Градиент

1. Производная по направлению

Рассмотрим функцию трех переменных u=f(x,y,z), определенную на множестве G. Пусть точка . Через точкуМ₀ проведём прямую l. Выберем произвольно на l точку М₁ и установим таким образом направление . Тогдаl – прямая с выбранным направлением.

ПустьМ(x,y,z) – переменная точка на прямой l. Через М₀М обозначим ориентированную длину отрезка М₀М, т.е. М₀М=|М₀М|, если направление отрезка совпадает с направлением l (точки М и М₁ лежат по одну сторону от точки М₀) и М₀М=-|М₀М|, если направление отрезка не совпадает с направлением l. Полное приращение функции:

.

Определение. Если существует конечный предел

,

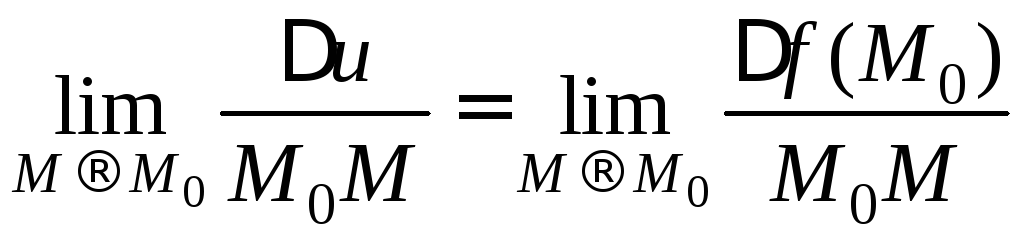то он называется производной функции f в точке М₀ по направлению l.

Обозначается .

Замечание. Производная функцииf(x) в точке х₀- это скорость изменения функции в точке х₀. Частная производная - скорость изменения функции в точкеМ₀ по направлению оси Ох; частная производная - скорость при функции в точкеМ₀ по направлению оси Оу, а - по направлению осиOz. Тогда - скорость изменения функции в точкеМ₀ по направлению l. Если направление l совпадает с положительным направлением оси Ох, то =. Аналогично для. Т.е. частные производные функции – это производные по направлению координатных осей.

Теорема (достаточное условие существования производной по направлению l). Если u=f(x,y,z) дифференцируема в точке М₀, то в этой точке существует производная по направлению, исходящему из точки М₀, и

, (1)

где - направляющие косинусы направленияl (координаты единичного вектора в этом направлении).

Доказательство.

Проведём через точкуМ₀прямуюl возьмём на ней точку М,- ориентированная длина.

.

По условию функцияf дифференцируема в точке М₀. Следовательно, её полное приращение можно записать в виде

, (2)

где при. Разделим (2) на:

. (3)

Пусть ММ₀. Тогда . Тогда (проекции на оси координат) стремятся к 0. Следовательно,. Значит, правая часть равенства (3) пристремится к. Это означает, что существует илевой части:. Переходя в (3) к, получим (1).

Пример. . Найти производную в точкеМ₀(1,-2,3) в направлении вектора, соединяющего точки А(1;2;3) и В(3;3;1).

(2,1,-2), , .

, ,

, ,

, ,

.

2. Градиент

Пусть функция u=f(x,y,z) определена и дифференцируема на множестве G.

Определение. Градиентом функции u=f(x,y,z) в точке М₀ называется вектор с координатами .

Обозначается или.

Итак, .

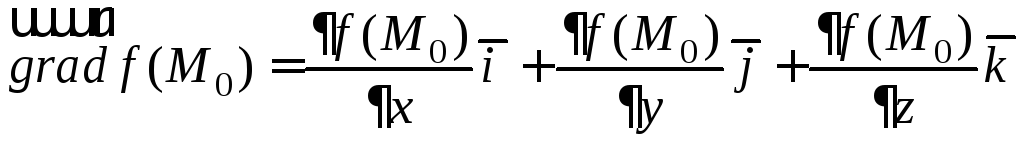Если функция f дифференцируема на G, то в каждой точке МG определён вектор . В этом случае говорят, что градиент функцииf образует векторное поле на G, и оно называется векторным полем градиентов.

Теорема. Если функция u=f(x,y,z) дифференцируема в точке М₀, то производная по направлению l в точке М₀ равна проекции градиента функцииf в этой точке на направление l.

Доказательство.

Т.к. функцияf дифференцируема в точке М₀, то в этой точке существуют производная по направлению l и градиент, т.е. имеем

,

.

Ч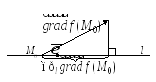ерезобозначим единичный вектор направления l: .

Тогда(скалярное произведение).

Т.к. , где- угол между векторамии, то, учитывая, чтоа, получим. Следовательно,.

Свойства градиента

1. Производная в данной точке М₀ по направлению l имеет наибольшее значение, если направление l совпадает с направлением градиента. Это наибольшее значение

.

2. Производная по направлению вектора, перпендикулярного к вектору градиента, равна нулю (следует из доказательства теоремы).

3. В каждой точке М₀ области определения функции градиент функции f направлен по нормали к поверхности уровня проходящей через эту точку.

4. ;

5. , гдес=const;

6.

Свойства 4-6 следуют из определения градиента и правил дифференцирования.