2. Дифференциалы высших порядков
Пусть z=f(x;y), где х, у – независимые переменные, определена на области G и имеет на этой области непрерывные частные производные. Тогда она дифференцируема, и ее дифференциал равен
,
где dx=Δx,
dy=Δy.
Следовательно, dz – функция четырех переменных: х, у, dx, dy. Зафиксируем dx и dy. Тогда dz=φ(x;y). Если функция f на G имеет непрерывные частные производные второго порядка, то функция dz=φ(x;y) на этой области имеет непрерывные частные производные, следовательно, она дифференцируема на G и имеет дифференциал.
Определение. Дифференциалом второго порядка d2z функции z=f(x;y) называется дифференциал от ее дифференциала первого порядка dz:
d2z=d(dz).
.
Т.к.
,
то
. (6)
Символическая
запись второго дифференциала:
.
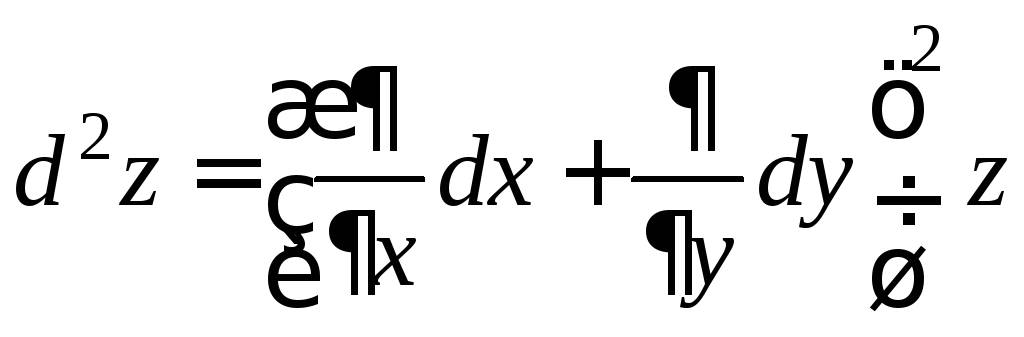Если функция f на G имеет непрерывные частные производные третьего порядка, то функция d2z=ψ(x;y) на этой области имеет непрерывные частные производные, следовательно, она имеет дифференциал. Дифференциал от этой функции называется дифференциалом третьего порядка функции z=f(x;y) и обозначается d3z. Таким образом,
.
Символическая
запись:
.
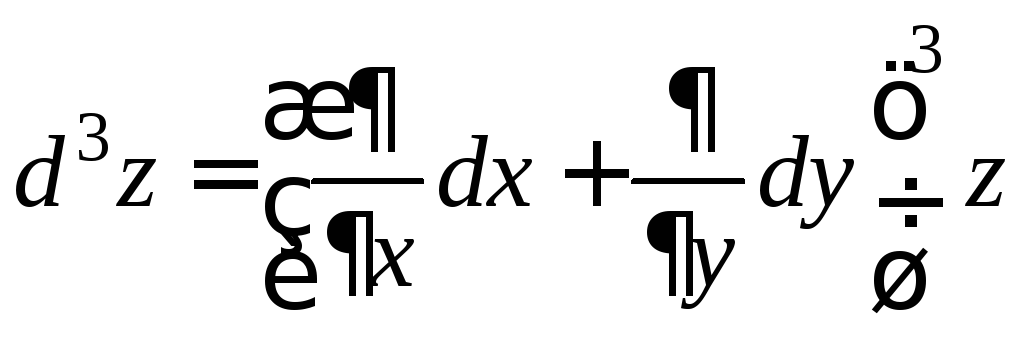Если функция f на G имеет непрерывные частные производные n-го порядка, то на G существует дифференциал n-го порядка, и он определяется с. о.: dnz=d(dn-1z).
.
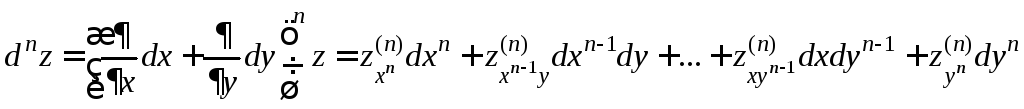Форма (6) записи дифференциала второго порядка неинвариантна, т. е не пригодна в случае, когда x и y являются функциями. Дифференциалы высших порядков также не обладают свойством инвариантности формы.
3. Формула Тейлора для функции двух переменных
Пусть функция F(t) в некоторой окрестности V(t0) имеет производные до (n+1)-го порядка включительно. Тогда справедлива формула Тейлора:
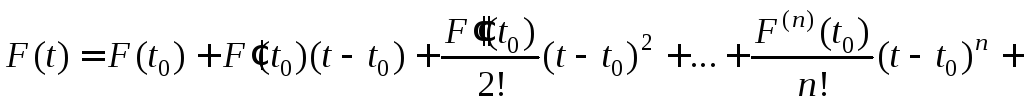
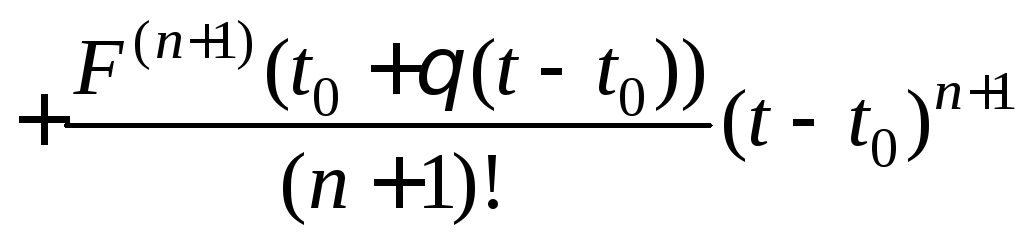. (7)
Обозначим t-t0=Δt, F(t)-F(t0)=ΔF(t0),
F'(t0)(t-t0)=F'(t0)Δt=dF(t0),
F''(t0)(t-t0)2=F''(t0)(Δt)2=d2F(t0) и т.д.
Тогда (7) можно записать в виде
,
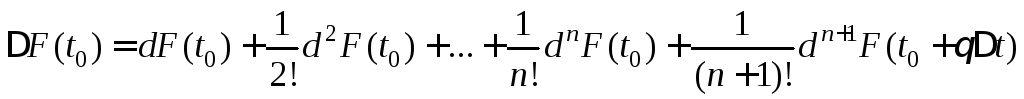где 0<θ<1.
(8)
В виде (8) формула Тейлора распространяется и на случай функций нескольких переменных.
Теорема.
Пусть функция z=f(x;y),
где х,
у
– независимые переменные, определена
и имеет непрерывные частные производные
до (n+1)-го
порядка включительно
в некоторой окрестности точки М(х0;y0)
Vδ(х0;y0).
Тогда Δх,
Δу,
удовлетворяющих условию
,
имеет место формула Тейлора:
,
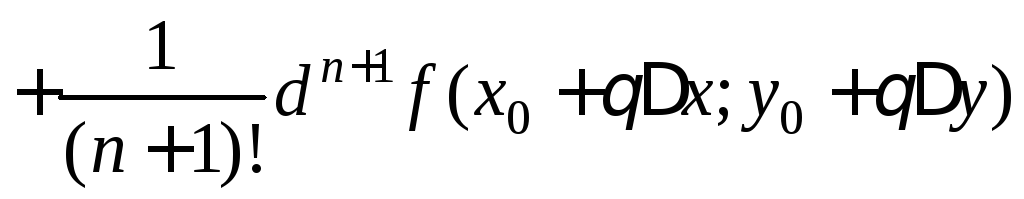где 0<θ<1.
(без доказательства)
Формула Тейлора имеет большое значение при вычислении приращений и значений функции с большой степенью точности.
§8. Неявные функции
1. Неявные функции одной переменной
Пусть дано уравнение F(x;y)=0, (1),
где F(x;y)
определена на
.
Пусть, например,G=[a,b;c,d]
- прямоугольник. Пусть х[a;b]
существует единственное значение y,
которое совместно с x
удовлетворяет уравнению (1). В этом случае
на [a;b]
определена однозначная функция y=f(x),
для которой равенство F(x;f(x))=0
верно х[a;b].
Определение. Функция y=f(x), определяемая уравнением (1), называется неявной функцией.
Е
сли
уравнение (1) разрешить относительноy,
то получим явную функцию y=f(x)
(функция справа известна), что далеко
не всегда можно сделать. Т.о., термины
«явная», «неявная» относятся к способу
задания функции.
Примеры.
1) x-6y+12=0,
где
,
F(x;y)=x-6y+12.
Разрешим уравнение относительно х:
- однозначная функция отх.
2)
F
(x;y)=
.Данное уравнение
представляет двузначную функцию
.
Если уравнение
рассматривать на
,
то оно определяет однозначную функцию
.
3)
не определяет функцииy=f(x).
Из примеров видно, что уравнение F(x;y)=0 не всегда определяет функцию y=f(x) (кроме того, далеко не всегда уравнение (1) можно разрешить относительно y). Поэтому необходимо знать условия существования неявной функции.
Теорема 1. (достаточные условия существования и дифференцируемости неявной функции). Пусть дано уравнение F(x;y)=0 (1), и выполнены условия:
1) функция F(x;y)
и ее частные производные
определены и непрерывны в некотором
прямоугольнике [x0-a,
x0+a;
y0-b,
y0+b];
2)
;
3)
.
Тогда справедливы следующие утверждения:
а) в некотором прямоугольнике (x0-, x0+; y0-, y0+) уравнение (1) определяет неявную функцию y=f(x);
б) f(x0)=y0;
в) функция y=f(x) непрерывна в промежутке [x0-; x0+];
г) функция y=f(x)
в промежутке [x0-;
x0+]
имеет непрерывную производную, причем
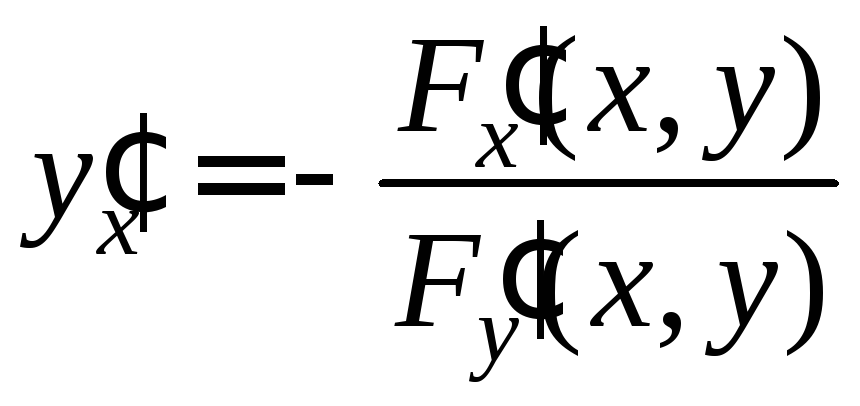. (2)
(без доказательства)
Замечание 1. Формулу (2) можно получить следующим образом. Продифференцируем равенство F(x;f(x))0 по x (F – сложная функция от x):
,
(2)
Замечание 2.
В уравнении (1) F(x;y)=0
переменные x
и y
равноправны. Следовательно, можно
ставить вопрос о существовании функции
.
В этом случае в теореме (1) надо изменить
условие 3) – требовать, чтобы
.
Но если одновременно
,
то нельзя утверждать, что уравнение (1)
определяет какую-либо неявную функцию.
Пример 1. Вычислить
производные первого и второго порядка
функции, заданной неявно уравнением
(x>0).
.
1
способ
вычисления
- по формуле (9).
.
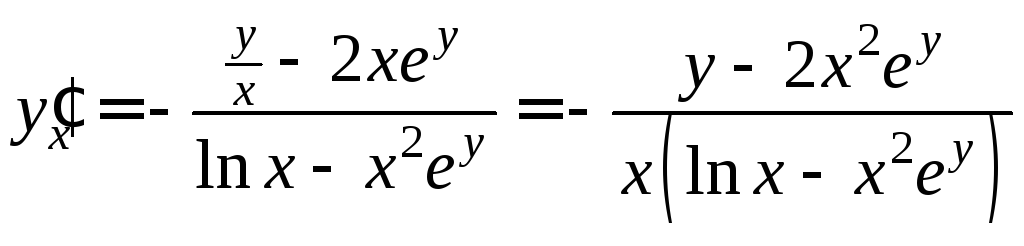2
способ
вычисления
.
Продифференцируем данное уравнение,
учитывая, что оно определяет функциюу=у(х).
(*) 
,
.
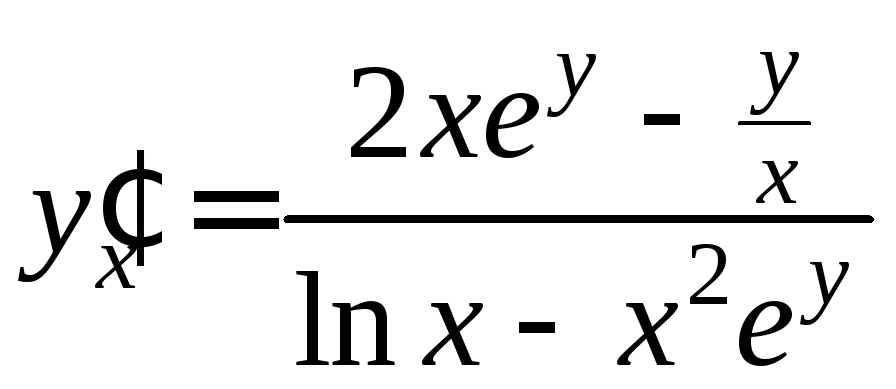Найдем
,
учитывая, чтоу=у(х),
а х
– независимая переменная:
.
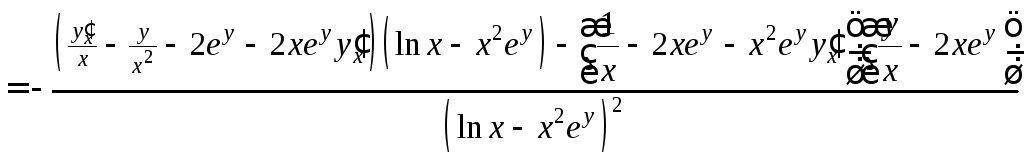Далее надо
преобразовать и подставить
.
Второй способ
вычисления
- продифференцировать равенство (*).