2. Уравнения касательной и нормали к кривой

Пусть дано уравнение (1) F(x;y)=0, и для функции F(x;y) в окрестности точки (х₀;y₀) выполнены условия теоремы 1. Тогда в окрестности точки х₀ V(х₀) уравнение (1) задает функцию у=f(х), определенную, непрерывную и дифференцируемую в некоторой окрестности точки х₀ и f(х₀)=y₀. Графиком этой функции является некоторая кривая. Так как существует , то существует касательная и нормаль к кривой (1).

Для функции y=f(x) уравнение касательной точке х₀ имеет вид:

, (3)

нормали: 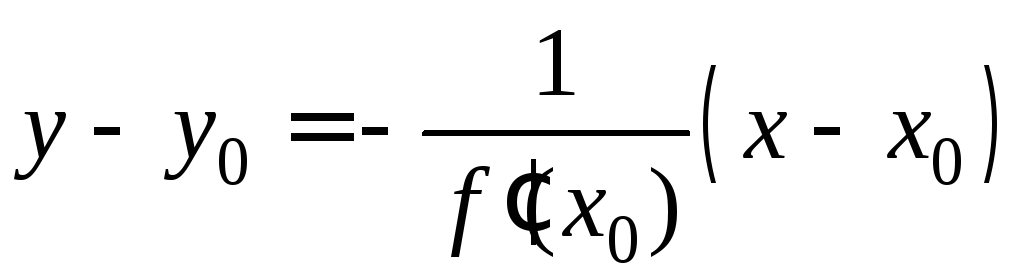. (4)

Из теоремы 1 следует 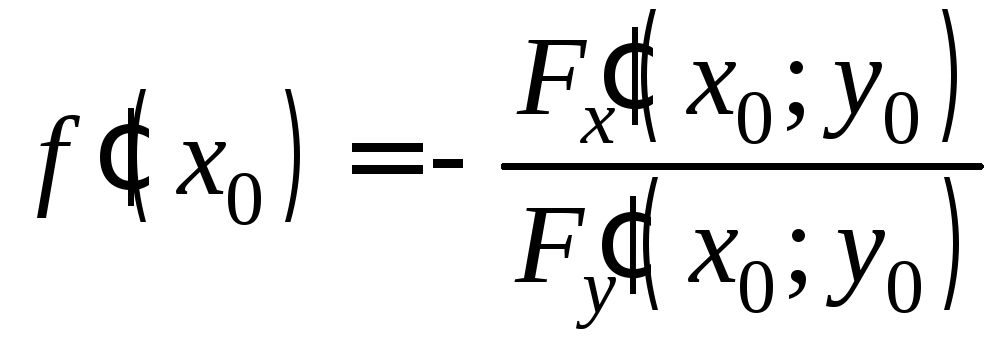. (5)

Подставляя (5) в (3), (4), получим 

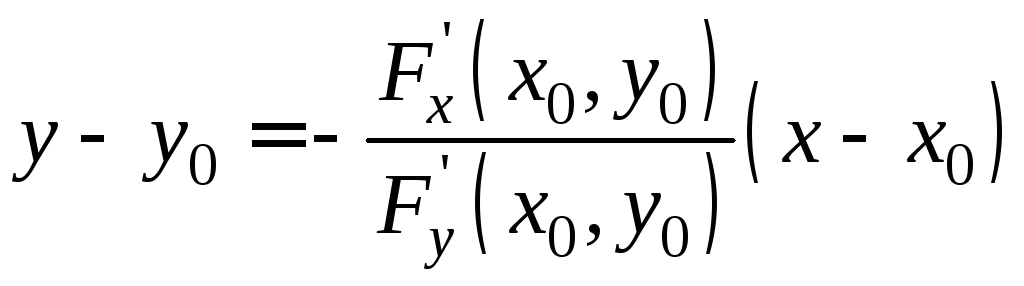
–уравнение касательной;

или

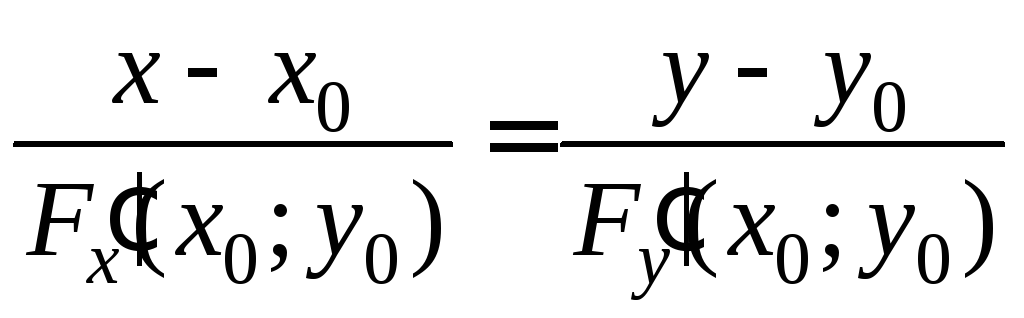–уравнение нормали.

3. Неявные функции нескольких переменных

Пусть дано уравнение . (6)

- функция (n+1)-й переменной. Если в каждой точке существует единственное значениеy, которое совместно с x удовлетворяет уравнению (13), то уравнение (13) на множестве G определяет функцию n переменных , (7)

и имеет место тождество наG.

Теорема 2 (достаточное условие существования и дифференцируемости неявной функции n переменных). Пусть функция F и ее частные производные непрерывны в некоторой окрестности точки, и пусть, а . Тогда уравнение (13) определяет функцию определенную, непрерывную и дифференцируемую в некоторой окрестности точки, причем, а частные производныенаходятся по формулам:

.

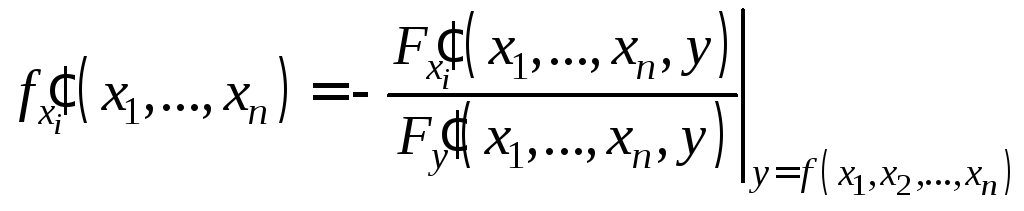
Рассмотрим частный случай. Пусть на дано уравнение

F(x;y;z)=0. (8)

Пусть это уравнение определяет неявную функцию z=f(x;y), дифференцируемую на , т.е. справедливо тождество (9)F(x;y;f(x;y))0. Правая часть (9) – сложная функция отх и у. в силу условий теоремы 2 (существуют непрерывные ) эта функция дифференцируема наD. Дифференцируя (9) по x, получим:

.

Отсюда 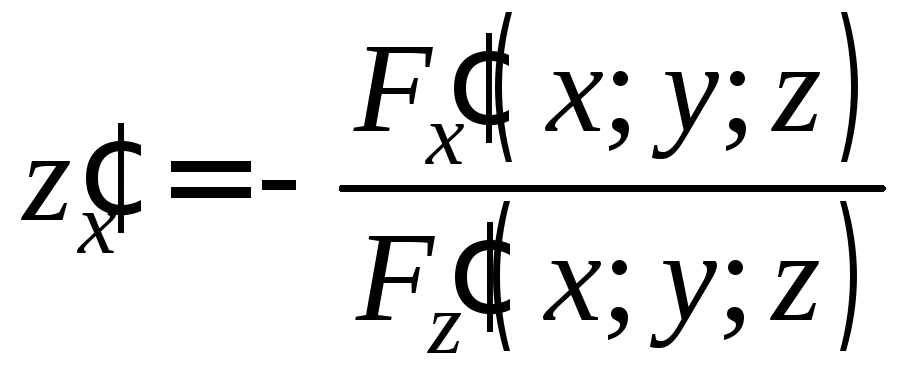. (10)

Дифференцируя (9) по y, получим:

.

Отсюда 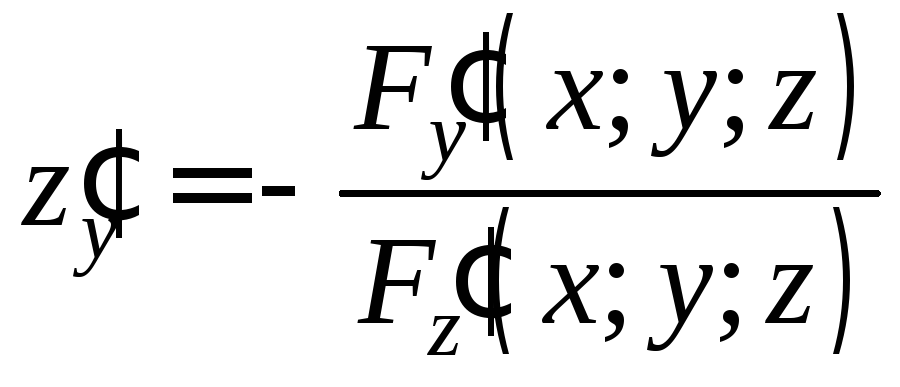. (11)

Пример 2. Пусть уравнение 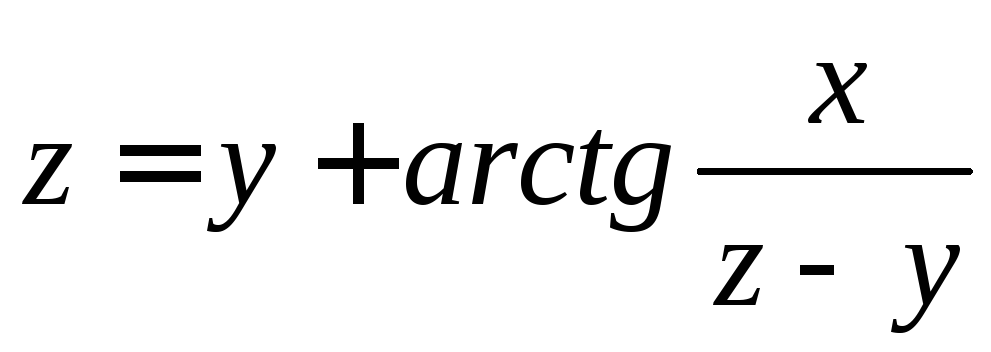определяет функциюz=f(x;y). Найти

 .

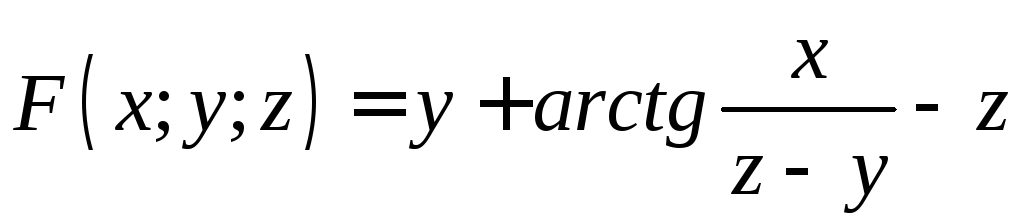По формулам (10), (11):

,

,

.

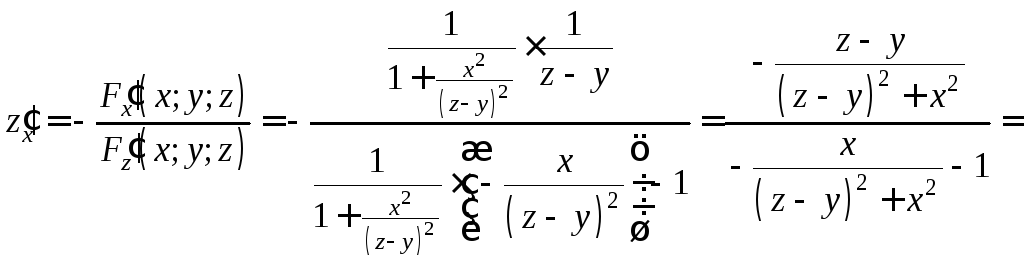
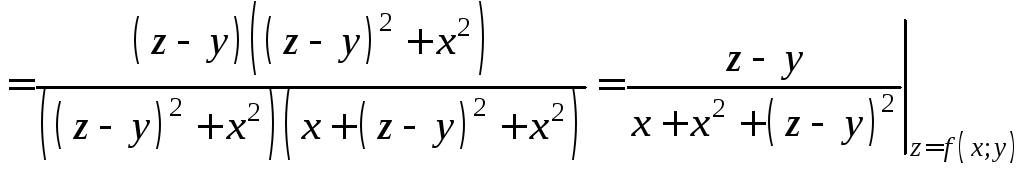
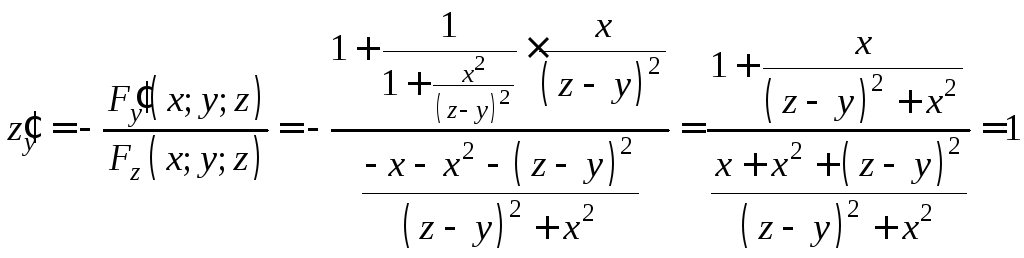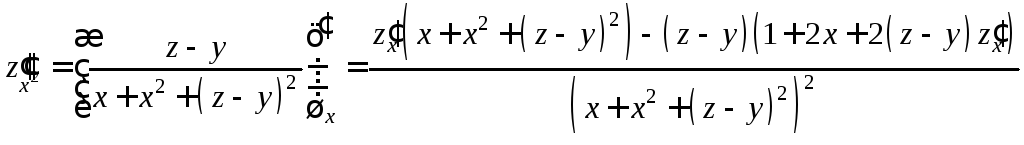Подставляя сюда выражение для и заменяя z на f(x;y), найдем .

Тогда .

4. Уравнения касательной плоскости и нормали к поверхности

Пусть уравнение (8) F(x;y;z)=0 определяет поверхность. Тогда (8) называется уравнением поверхности.

Пусть в окрестности (x₀;y₀;z₀) выполняется условия теоремы 2. Тогда в окрестности точки (x₀;y₀) определена функция z=f(x;y), дифференцируемая в этой окрестности. Тогда поверхность z=f(x;y) имеет касательную плоскость и нормаль в точке (x₀;y₀).

–уравнение касательной плоскости,

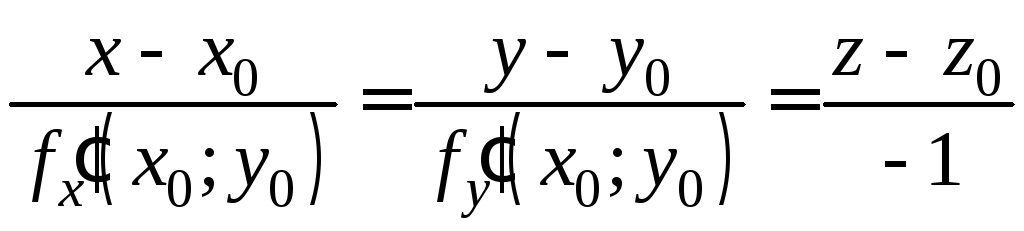–уравнение нормали.

Так как 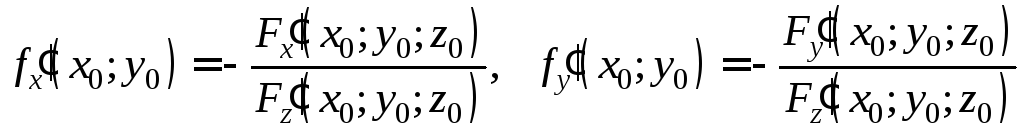, то

–

уравнение касательной плоскости,

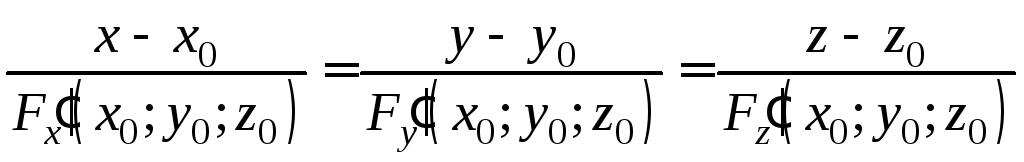–уравнение нормали.

Неявные функции могут определяться системой функциональных уравнений.

§ 9. Экстремум функции нескольких переменных

1. Понятие экстремума, необходимое и достаточное условия

Пусть функция z=f(x;y) задана в некоторой окрестности точки M₀(x₀;y₀) V(M₀).

Определение 1. Функция z=f(x;y) имеет в точке M₀(x₀;y₀) строгий максимум (строгий минимум), если , такая, чтовыполнено неравенствоf(x;y)<f(х₀;y₀) (f(x;y)>f(х₀;y₀)).

Определение 2. Функция z=f(x;y) имеет в точке M₀(x₀;y₀) максимум (минимум), если , такая, чтовыполнено неравенствоf(x;y)f(х₀;y₀) (f(x;y)f(х₀;y₀)).

Определение 3. Функция z=f(x;y) имеет в точке M₀(x₀;y₀) (строгий) экстремум, если она имеет в этой точке (строгий) максимум или (строгий) минимум.

Точку М₀ называют точкой (строгого) экстремума, а значение функции в ней, т.е. f(M₀) – (строгим) экстремумом.

Теорема 1 (необходимое условие экстремума). Пусть функция z=f(x;y) достигает экстремума в точке _M0(_x0;_y0). Если в этой точке существуют частные производные и , то они в этой точке равны нулю, то есть =0и =0.

Доказательство.

Пусть z=f(x;y) имеет в точке _M0(_x0;_y0) максимум. Тогда , такая, чтовыполнено

f(x;y)f(х₀;y₀). (1)

Рассмотрим точки окрестности V_(M₀), для которых y=y₀. На этом множестве точек, т.е. на , функцияf(x;y) превращается в функцию f(x;y₀) одной переменной х. Из (1) следует, что f(x;y₀)f(х₀;y₀) . Это означает, что функция одной переменной f(x;y₀) имеет в точке х₀ максимум. По условию . Она совпадает с в точке х₀, т.е =. На основании необходимого условия экстремума функции одной переменной =0. Следовательно, =0.

Аналогично, рассмотрим точки окрестности V_(M₀), для которых х=х₀. На этом множестве точек, функция f(x;y) становится функцией f(x₀;y) одной переменной у. Из (1) следует, что f(x₀;y)f(х₀;y₀) . Значит, функция одной переменной f(x₀;y) имеет в точке у₀ максимум. По необходимому условию экстремума функции одной переменной =0. Следовательно, =0.

Замечание. Если функция z=f(x;y) дифференцируема в точке (х₀;y₀), то условие 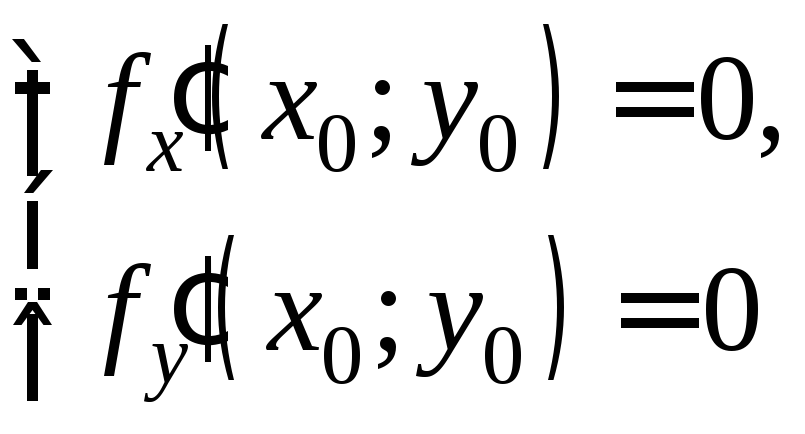равносильно условиюdf(х₀;y₀)=0.

Следствие. Если функция z=f(x;y) имеет экстремум в точке (х₀;y₀) и дифференцируема этой точке, то df(х₀;y₀)=0.

Определение 3. Точки, в которых частные производные равны нулю, называются стационарными точками функции z=f(x;y).

Определение 4. Точки, в которых частные производные равны нулю (или не существуют) называются критическими точками функции z=f(x;y).

Из теоремы 1 и определения 3 следует, что если функция дифференцируема, то точки экстремума являются стационарными точками. Обратное неверно. Не всякая стационарная точка является точкой экстремума.

Пример.  Рассмотрим функцию z=f(x;y)=x²-y², f(0;0)=0.

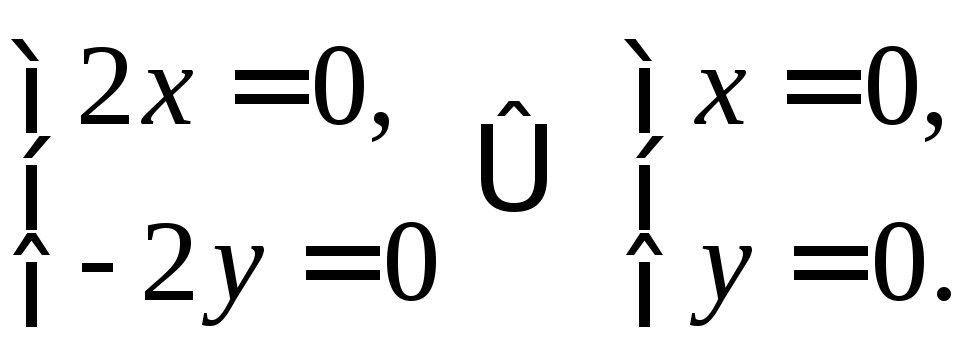
,  (0;0) – стационарная точка.

Рассмотрим . На оси Ох f(x;0)=x²>0, на оси Оу f(0;y)=-y²<0. Следовательно, в любой окрестности есть значения функции, как большиеf(0;0)=0, так и меньшие f(0;0)=0. Значит, точка (0;0) не может быть точкой экстремума. 

Теорема 2 (достаточное условие экстремума).(без доказательства)

Пусть функция z=f(x;y) определена и имеет непрерывные частные производные до второго порядка включительно в некоторой окрестности точки М₀(x₀;y₀) V(x₀;y₀). Пусть М₀(x₀;y₀) - стационарная точка, то есть и . Обозначим

.

Тогда

1) если то z=f(x;y) имеет в точке М₀(x₀;y₀) экстремум, причем при A<0 (C<0)- локальный максимум, при - локальный минимум;

2) если , то точка М₀(x₀;y₀) не является точкой экстремума;

3) если , то никакого заключения о характере стационарной точки сделать нельзя, требуются дополнительные исследования.

Теорема 3.Пусть df(х₀;y₀)=0. Если d²f(х;y) сохраняет знак в некоторой достаточно малой окрестности точки (х₀;y₀), то в этой точке функция имеет строгий экстремум, причем, если d²f(х₀;y₀)<0, то строгий максимум, а если d²f(х₀;y₀)>0, то строгий минимум.

В таком виде достаточное условие экстремума переносится на случай функций любого числа переменных.

Пример 1. Исследовать функцию f(x;y)=xy(a-x-y), a>0 на экстремум.

 .

Найдем стационарные точки.

f_x=y(a-x-y)-xy=y(a-2x-y), f_y=x(a-x-y)-xy=x(a-x-2y)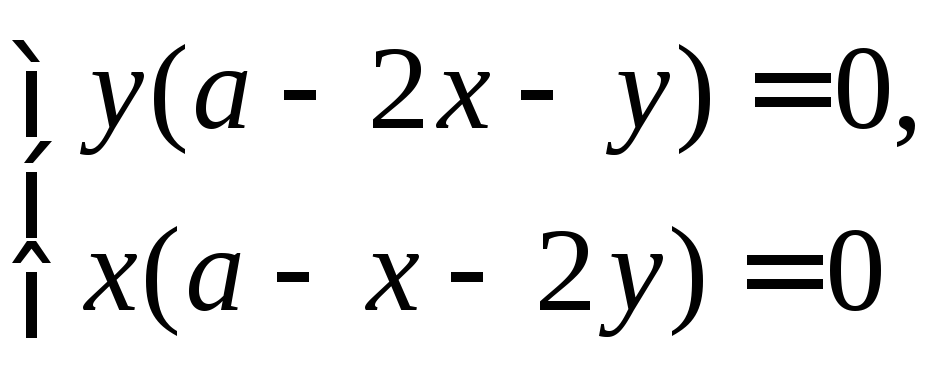

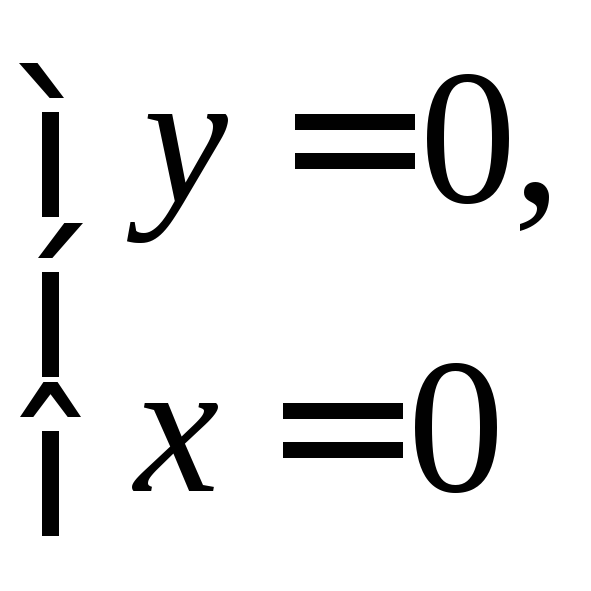
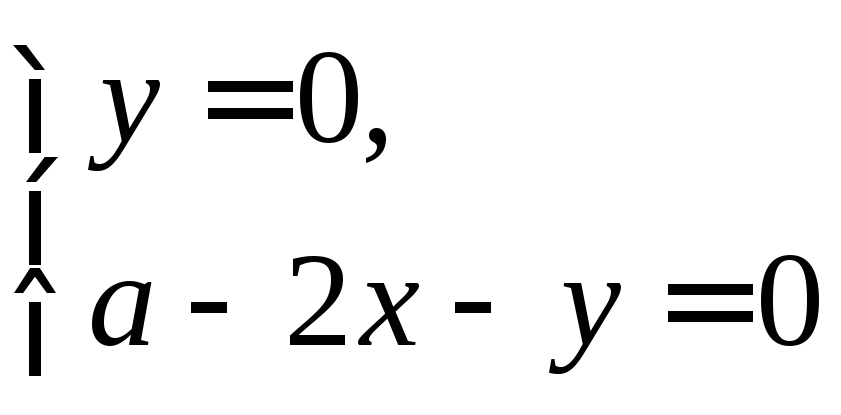
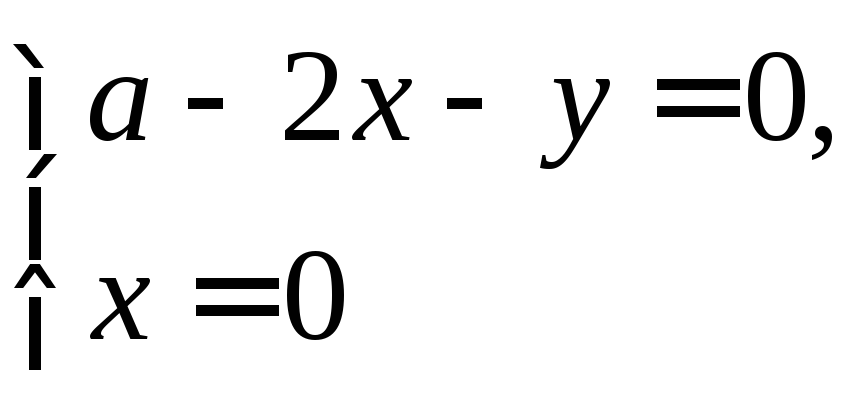
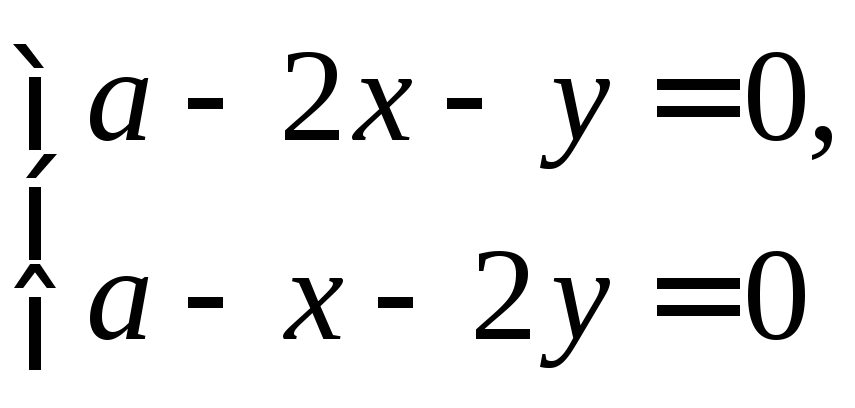
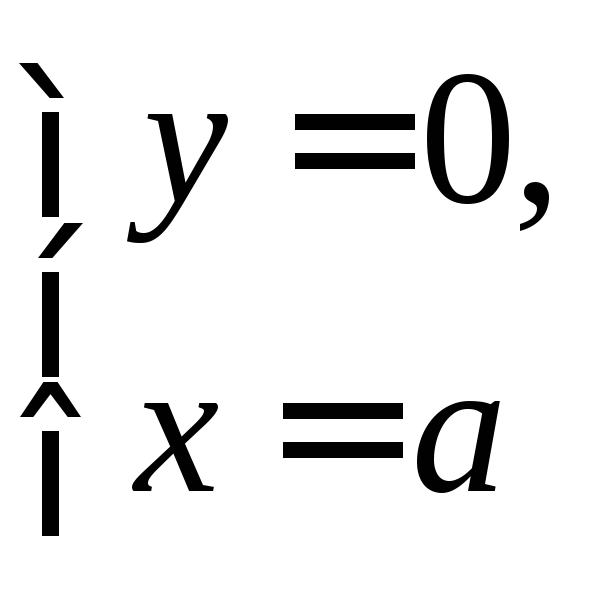
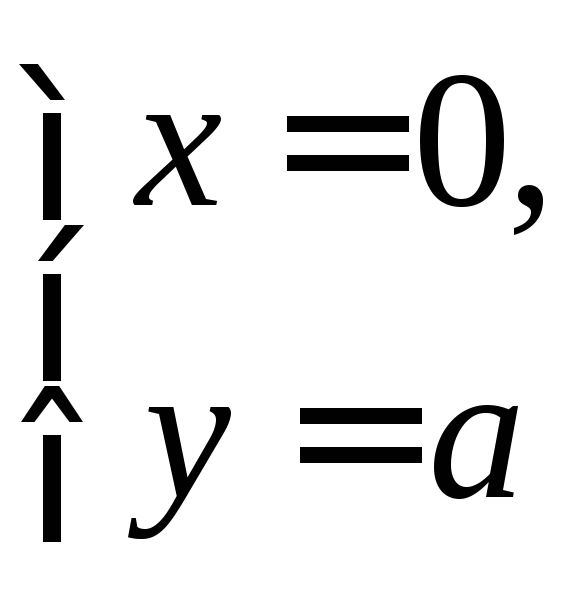
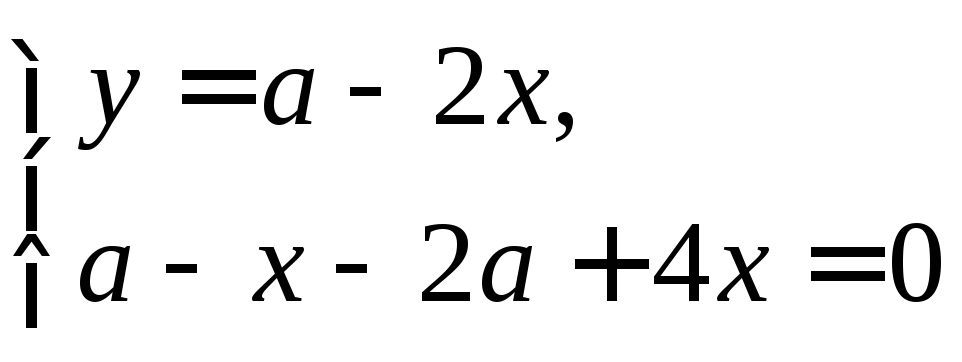
Стационарные точки: О(0;0), М(а;0), N(0;a), .

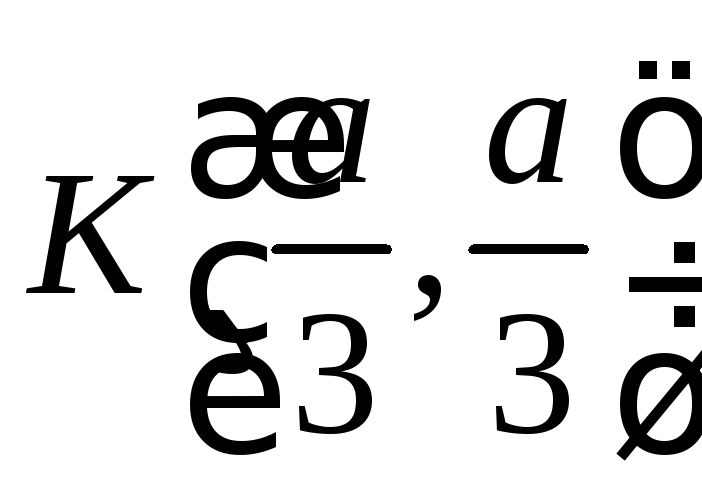Проверим, являются ли они точками экстремума.

, ,.

О(0;0): А=0, В=а, С=0, АС-В²=0-а²<0  экстремума нет;

М(а;0): А=0, В=-а, С=-2а, АС-В²=0-а²<0  экстремума нет;

N(0;a): А=-2a, В=-а, С=0, АС-В²=0-а²<0  экстремума нет;

: , , ,

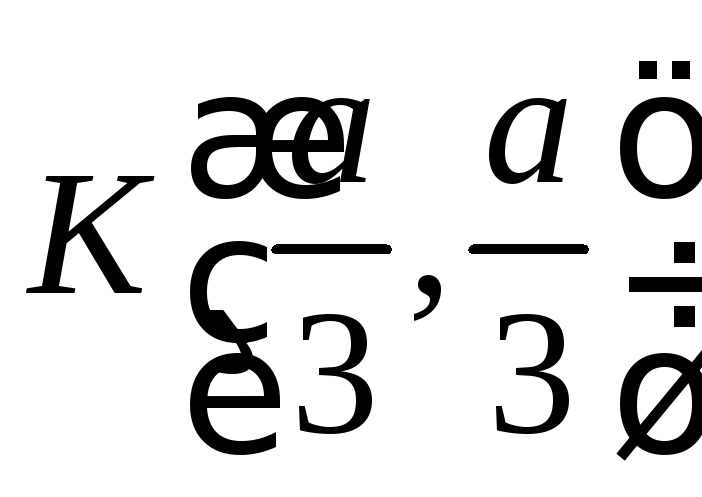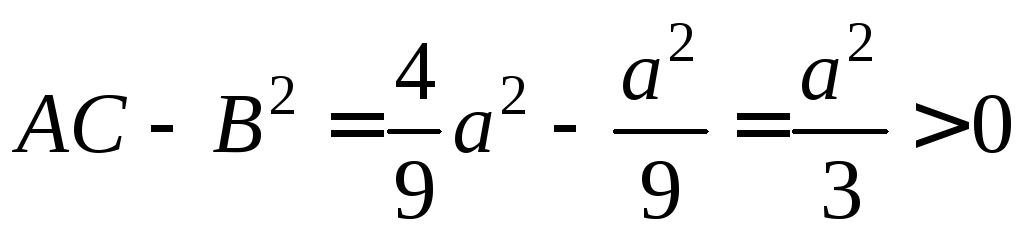К – точка экстремума, т.к. A<0, то - точка максимума.