Ряды

I. Числовые ряды

§1. Основные понятия

1. Понятие числового ряда. Сходящиеся и расходящиеся ряды

Пусть - числовая последовательность. Образуем из нее бесконечную сумму

, (1)

которая называется числовым рядом. Числа (члены последовательности) называютсячленами ряда (1), a - общим членом ряда (1).

Суммы

S₁=a₁;- первая частичная сумма ряда (1)

S₂=a₁+a₂;

S₃=a₁+a₂+a₃;

……………..

S_n=a₁+a₂+…+a_n - n-я частичная сумма

называют частичными суммами ряда (1).

Так как число слагаемых в ряде (1) бесконечно, то можно составить последовательность частичных сумм.

Определение. Ряд (1) называется сходящимся, если существует конечный предел последовательности его частичных сумм, то есть:

При этом число S называют суммой ряда (1) и пишут .

В противном случае ряд (1) называетсярасходящимся. Для расходящегося ряда понятие суммы не определено.

Задача установления сходимости или расходимости ряда – одна из главных задач теории рядов.

Рассмотрим примеры исследования рядов на сходимость с помощью определения.

Пример 1. Исследовать на сходимость ряд

.

Δ Представим n-й член ряда в виде суммы простейших дробей

.

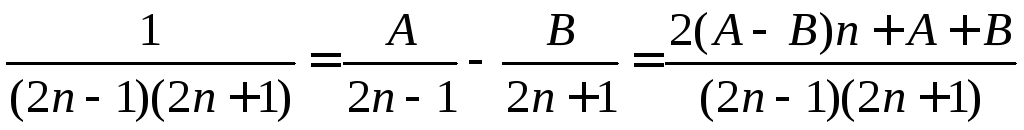Приравнивая коэффициенты при одинаковых степенях n, получим



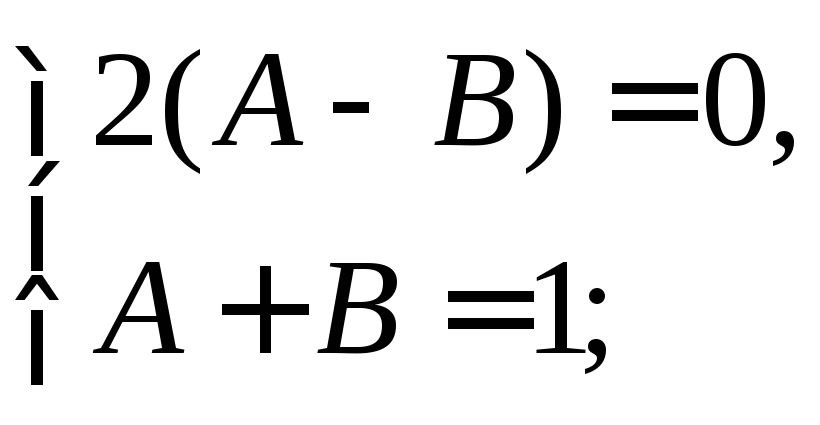
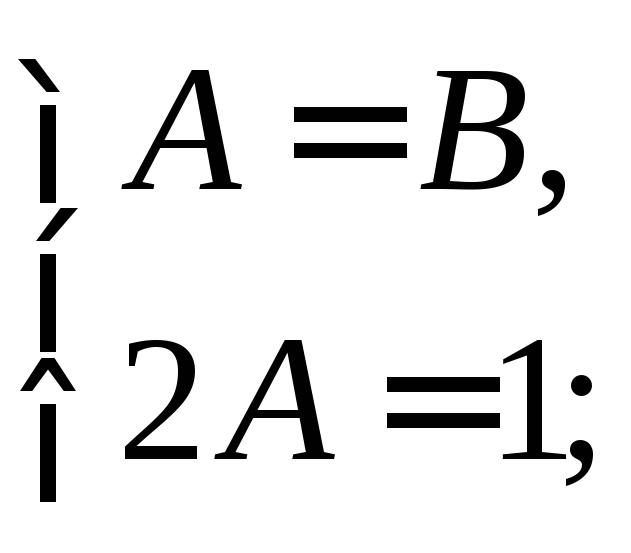
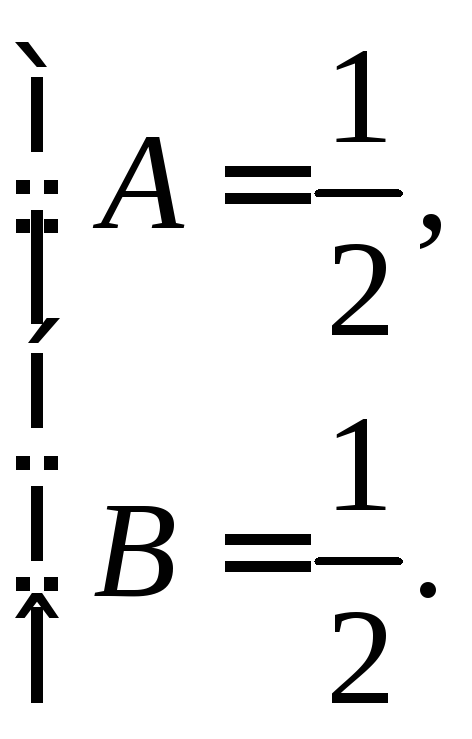
Значит,

.

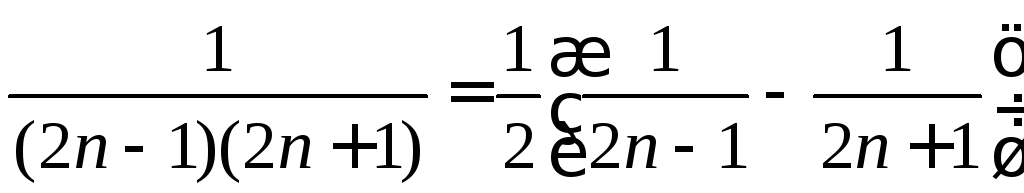Тогда n-я частичная сумма примет вид

.

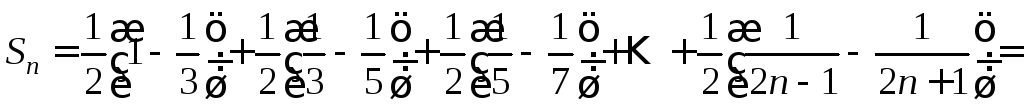
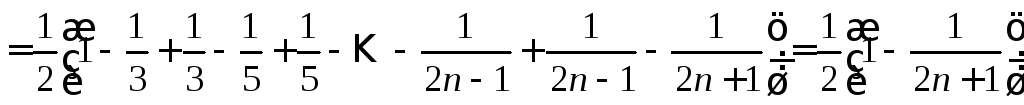Следовательно, .

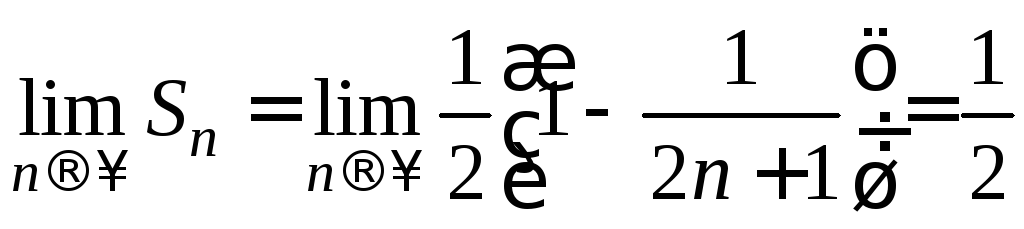Значит, согласно определению ряд сходится. Сумма ряда

Δ

Пример 2. Доказать, что ряд расходится.

Δ

Значит, ряд расходящийся. Δ

Пример 3. Исследовать ряд на сходимость.

Δ Данный ряд называется геометрическим. (, – фиксированные числа). Геометрический ряд является суммой членов геометрической прогрессии. Как известно,

.

Рассмотрим 4 случая

1) ТогдаСледовательно,.

Значит, при рядсходится и его сумма.

2) . Тогдаи, значит,. Следовательно, ряд прирасходится.

3) q=1. Тогда данный ряд имеет вид

,

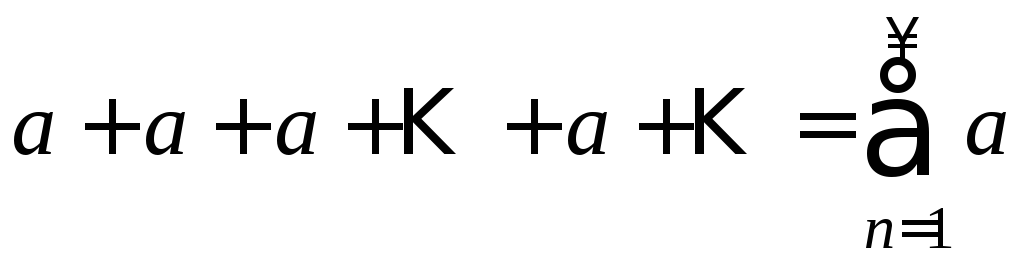. Значит, ряд при расходится.

4) q=-1. Ряд примет вид

;

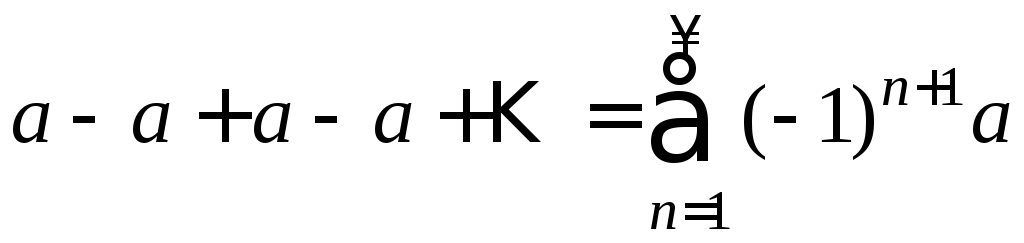Значит,

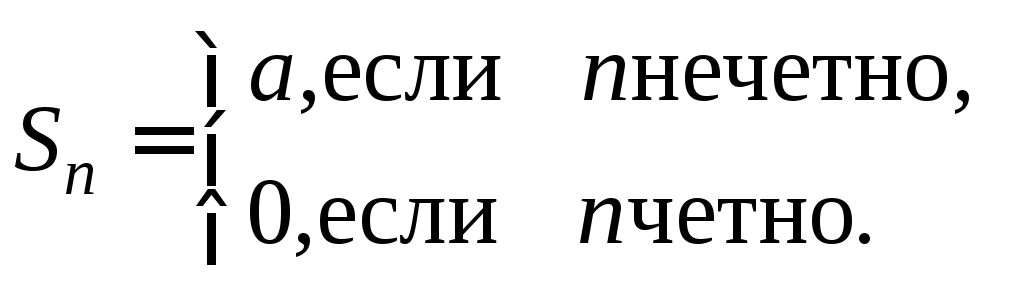
{S_n}: a;0;a;0;… .

Значит, и в этом случае ряд расходится.

Итак, геометрический ряд (сходится при,

расходится при . Δ

2. Остаток сходящегося ряда

Рассмотрим ряд (1):

(1)

Отбросим в этом ряде n членов подряд, начиная с первого. Получим ряд

(2)

Ряд (2) называется n-м остатком ряда (1).

Если -й остаток (2) ряда (1) сходится, то его сумму обозначают.

Теорема 1. Ряд (1) сходится тогда и только тогда, когда сходится любой из его остатков (2). При этом если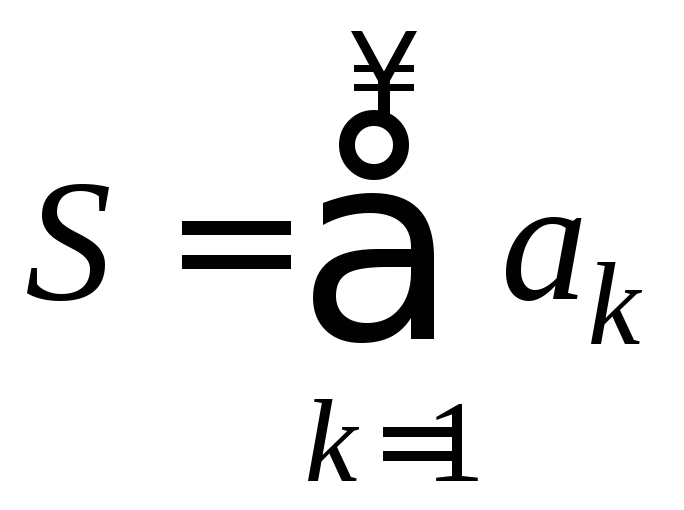,,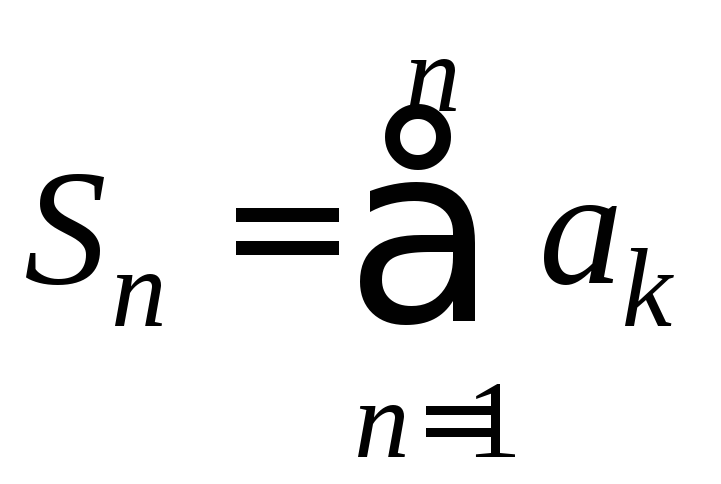, то

. (3)

Из теоремы 1 следует, что отбрасывание или добавление любого конечного числа первых членов ряда не влияет на его сходимость или расходимость.

Теорема 2. Если ряд (1) сходится, то его остаток имеет предел, равный 0:.

Доказательство.

Пусть ряд (1) сходится. Тогда, согласно теореме 1, сходится его остаток (2) и имеет место равенство (3): .

Отсюда .

Переходя к , получим:.

Из равенства следует, что абсолютная погрешность, допускаемая при замене суммыS сходящегося ряда (1) его частичной суммой , равна. Т. о., для оценки этой погрешности достаточно оценить

3. Свойства сходящихся рядов

Определение. Суммой рядов (A) и (B) называется ряд (A+B).

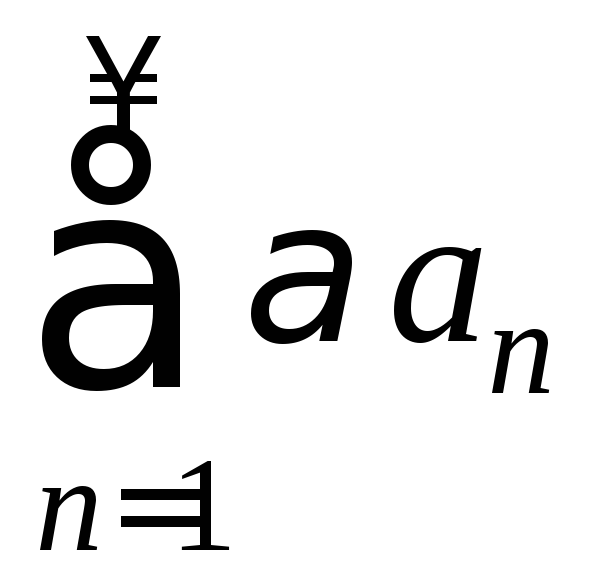Произведением ряда на числоназывается ряд(A).

Теорема 3. Если ряды исходятся, то сходится и их сумма, причем.

Доказательство.

Так как ряды исходятся, то

, .

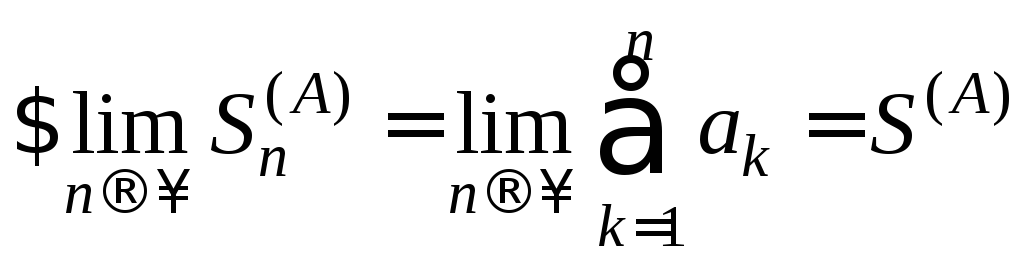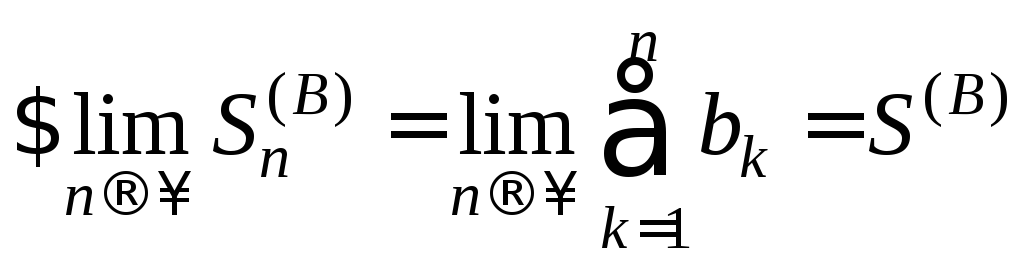Тогда .

следовательно, ряд сходится и.

Теорема 4. Если ряд , сходится,, то рядсходится и

.

Доказательство.

Так как ряд сходится, то .

тогда .

То есть ряд 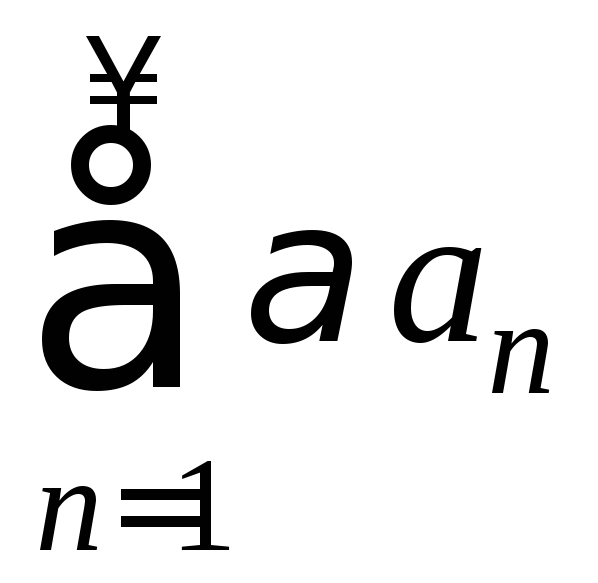сходится, и.

Пример 4. Исследовать на сходимость ряд . В случае сходимости найти сумму ряда.

Δ По теореме 3 и теореме 4

.

Ряды в правой части – геометрические, сходятся. Следовательно данный ряд сходится. Найдем его сумму.

, .

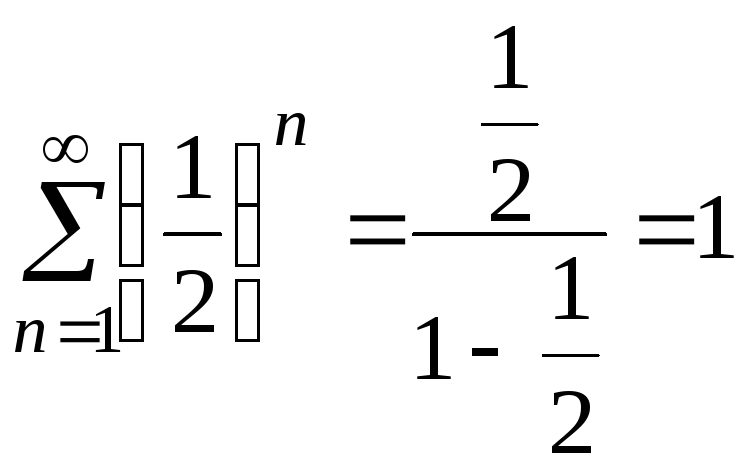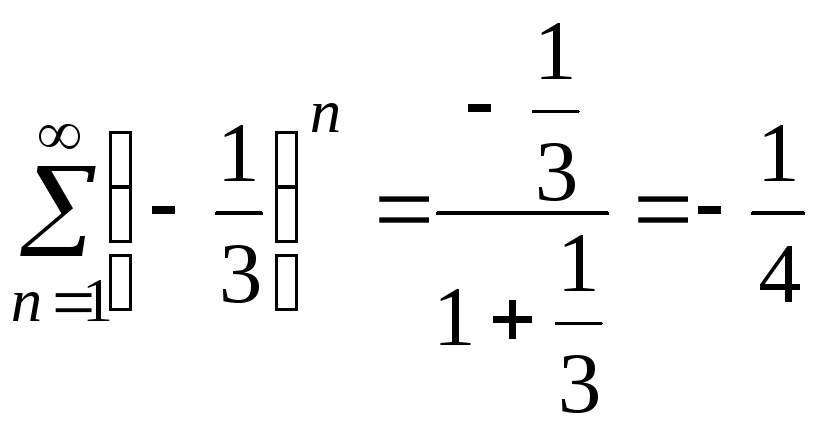тогда . Δ

Замечание. Сумма двух расходящихся рядов не обязательно является расходящимся рядом. Например, ряды расходятся, а- сходится.