
Лекция №2
Тема: Типы дифференциальных уравнений первого порядка.
Вопросы:
1. Простейшие типы уравнений первого порядка: не содержащие искомую функцию, не содержащие явно независимую переменную.
2. Дифференциальная форма ДУ. Уравнения с разделенными переменными.
3. Уравнения с разделяющимися переменными.
4. Однородные уравнения.
5. Линейные уравнения и уравнения Бернулли.
1. Уравнение вида
![]() , (1)
, (1)
т.е. уравнение, не содержащее искомую функцию.
Предположим, что
функция
![]() непрерывна при
непрерывна при
![]() .
Как известно из курса интегрального
исчисления, все первообразные для
.
Как известно из курса интегрального
исчисления, все первообразные для
![]() ,
а, следовательно, все решения уравнения
выражаются формулой
,
а, следовательно, все решения уравнения
выражаются формулой
![]() ,
,
![]() .
.
Если в качестве первообразной взять определенный интеграл с переменным верхним пределом х
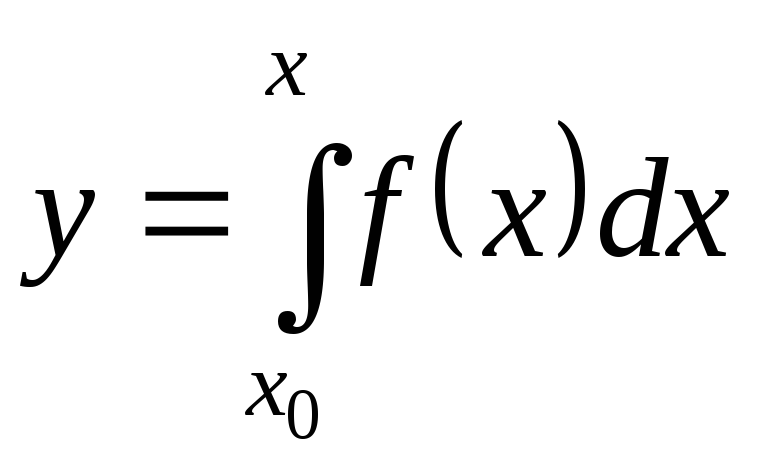 ,
,
где
![]() ,
то общее решение уравнения (1) примет
вид:
,
то общее решение уравнения (1) примет
вид:
 .
.
Как только в полосе
![]() зададим точку
зададим точку
![]() ,
через которую должна проходить
интегральная кривая, постоянная С
определится единственным образом:
,
через которую должна проходить
интегральная кривая, постоянная С
определится единственным образом:
![]() .
Значит, через каждую точку
.
Значит, через каждую точку
![]() этой полосы проходит одна и только одна
интегральная кривая, а именно
этой полосы проходит одна и только одна
интегральная кривая, а именно
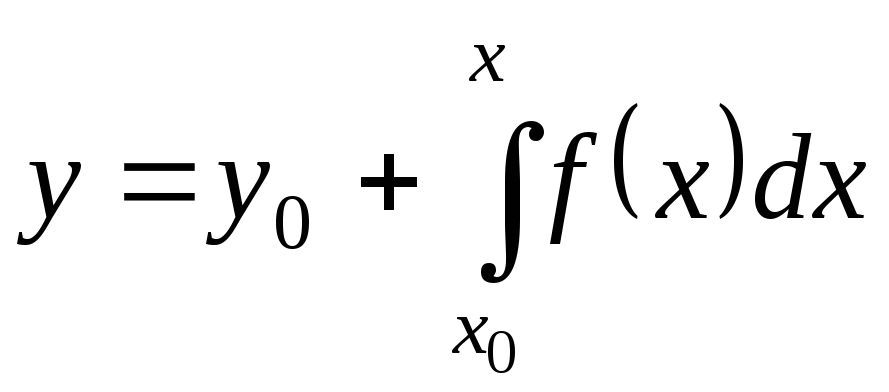 .
.
Это есть общее решение уравнения (1) в форме Коши.
Каждая из указанных
формул общего решения дает возможность
найти решение, удовлетворяющее начальному
условию
![]() при
при
![]() ,
где
,
где
![]() .
.
Пример.
Найти общее решение уравнения
![]() и выделить решение, удовлетворяющее
начальному условию
и выделить решение, удовлетворяющее
начальному условию
![]() при
при
![]() ,
т.е. выделить интегральную кривую,
проходящую через точку
,
т.е. выделить интегральную кривую,
проходящую через точку
![]() .
.
Решение. Правая часть уравнения непрерывна при всех х. Общее решение имеет вид
![]() ,
,
![]() .
.
Подставляя в
полученное уравнение вместо х
и у
числа 0 и1, имеем
![]() ,
откуда
,
откуда
![]() .
Следовательно, искомым решением будет
.
Следовательно, искомым решением будет
![]() .
.
2. Уравнение вида
![]() , (2)
, (2)
где
![]() - непрерывная в некотором интервале
- непрерывная в некотором интервале
![]() функция. Предположим сначала, что
функция. Предположим сначала, что
![]() отлична от нуля на всем интервале
отлична от нуля на всем интервале
![]() .
Тогда, не нарушая равносильности,
уравнение (2) можно переписать в виде
.
Тогда, не нарушая равносильности,
уравнение (2) можно переписать в виде
![]() ,
,
откуда
![]() , (3)
, (3)
или
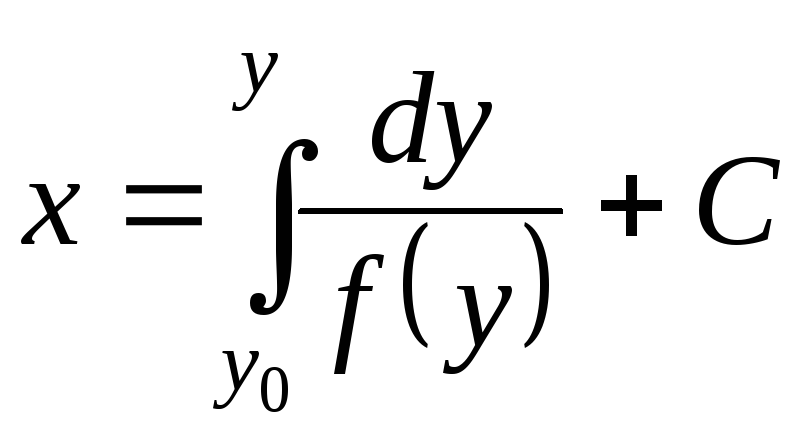 , (4)
, (4)
где
![]() .
Каждое из соотношений (3), (4) является
общим интегралом уравнения (2).
.
Каждое из соотношений (3), (4) является
общим интегралом уравнения (2).
Если правая часть
уравнения (2) обращается в нуль при
![]() ,
причем
,
причем
![]() ,
то оно, очевидно, имеет решение
,
то оно, очевидно, имеет решение
![]() , (5)
, (5)
так как обе части
этого уравнения обращаются в нуль при
![]() .
Решение (5) при переходе от (2) к (3) можно
потерять. Поэтому следует после
интегрирования уравнения
.
Решение (5) при переходе от (2) к (3) можно
потерять. Поэтому следует после
интегрирования уравнения
![]() рассмотреть уравнение
рассмотреть уравнение
![]() .
.
Пример. Решить
уравнение
![]() .
.
Решение. Правая часть этого уравнения непрерывна при всех значениях у и не обращается в нуль, поэтому потери решений быть не может. интегрируя, имеем
![]() ,
,
откуда
![]() .
.
Это есть общий интеграл уравнения.
Определение 1. Общее решение дифференциального уравнения, записанное в виде, не разрешенном относительно искомой функции у,
![]() ,
,
называется общим интегралом этого уравнения.
Возвращаясь к
примеру, отметим, что поскольку
![]() ,
то переменные х
и С
связаны условием
,
то переменные х
и С
связаны условием
![]() .
.
Полученный общий интеграл можно записать в виде, разрешенном относительно у, не забывая при этом указанного ограничения на х и С. Получим
![]() ,
,
![]() .
.
Таким образом, мы получили общее решение исходного уравнения.
Дифференциальное
уравнение, в нормальной форме, т.е.
разрешенное относительно производной,
можно записать в виде
![]() или
или
![]()
это уравнение в дифференциальной форме.
