Гоу впо
«Брянский государственный университет
имени академика И.Г.Петровского»
УТВЕРЖДАЮ:
Зав. кафедрой____________________
« » 2011 года Курс 2, ИТ, ФМФ
Экзаменационный билет № 1
по дифференциальным и разностным уравнениям
Понятие дифференциального уравнения в частных производных. Задача Коши и теорема Ковалевской. Геометрическая трактовка.
Простейшие типы уравнений первого порядка: не содержащие искомую функцию, не содержащие явно независимую переменную.
Решить дифференциальное уравнение
.
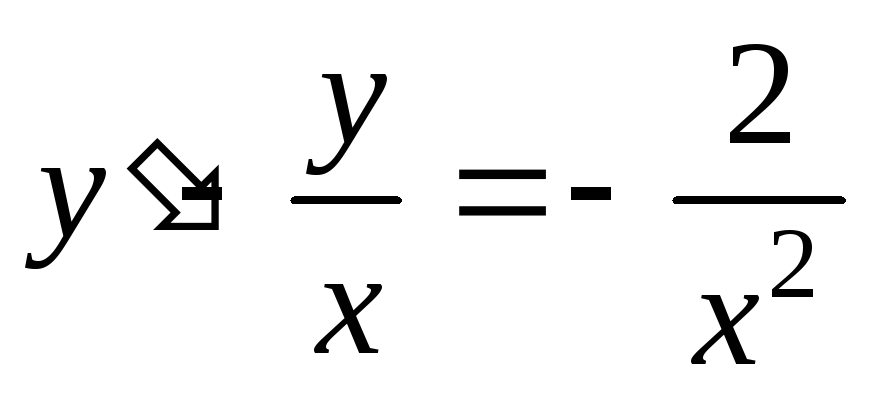Экзаменатор_________________
ГОУ ВПО
«Брянский государственный университет
имени академика И.Г.Петровского»
УТВЕРЖДАЮ:
Зав. кафедрой____________________
« » 2011 года Курс 2, ИТ, ФМФ
Экзаменационный билет № 2
по дифференциальным и разностным уравнениям
Линейные дифференциальные уравнения в частных производных. Свойства их решений. Векторные линии и векторные поверхности, характеристики. Примеры.
ДУ первого порядка. Нормальная форма записи. Задача Коши и теорема Пикара. Общее, частное и особое решения ДУ.
Решить дифференциальное уравнение
.
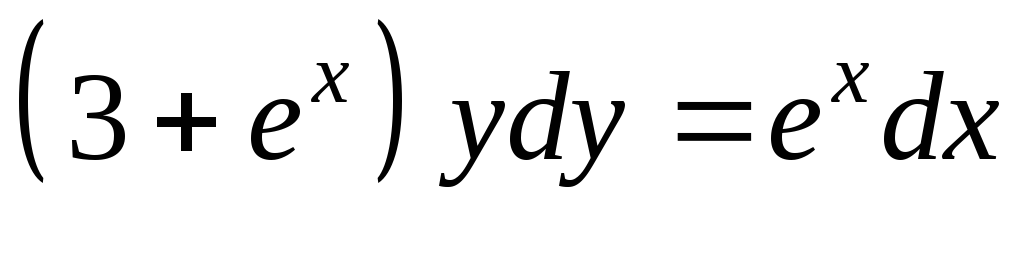Экзаменатор_________________
ГОУ ВПО
«Брянский государственный университет
имени академика И.Г.Петровского»
УТВЕРЖДАЮ:
Зав. кафедрой____________________
« » 2011 года Курс 2, ИТ, ФМФ
Экзаменационный билет № 3
по дифференциальным и разностным уравнениям
Геометрические и физические задачи, приводящие к понятию дифференциального уравнения.
Уравнения гиперболического типа. Канонический вид.
Решить задачу Коши
.
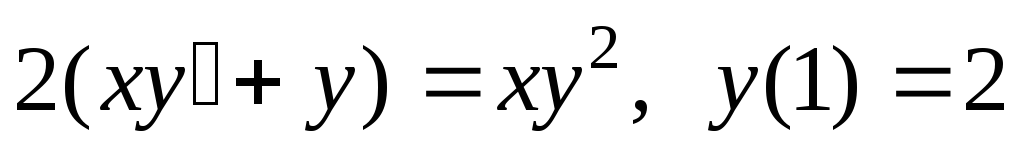Экзаменатор_________________
ГОУ ВПО
«Брянский государственный университет
имени академика И.Г.Петровского»
УТВЕРЖДАЮ:
Зав. кафедрой____________________
« » 2011 года Курс 2, ИТ, ФМФ
Экзаменационный билет № 4
по дифференциальным и разностным уравнениям
Основные понятия теории дифференциальных уравнений: дифференциальное уравнение, порядок ДУ, решение ДУ, интегральная кривая, начальные данные.
Классификация дифференциальных уравнений в частных производных второго порядка. Примеры. Типы краевых задач для дифференциальных уравнений
Найти поверхность, удовлетворяющую данному уравнению и проходящую через данную линию
,
,
.
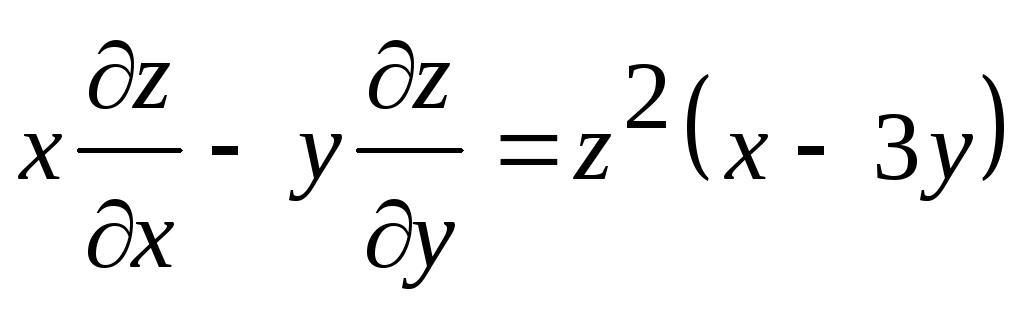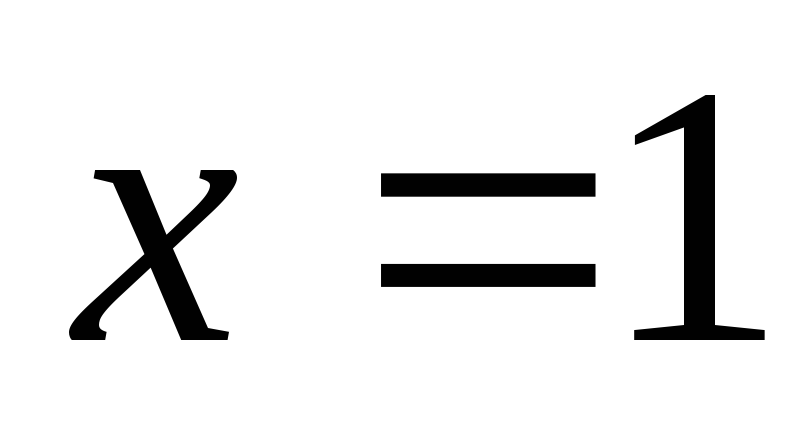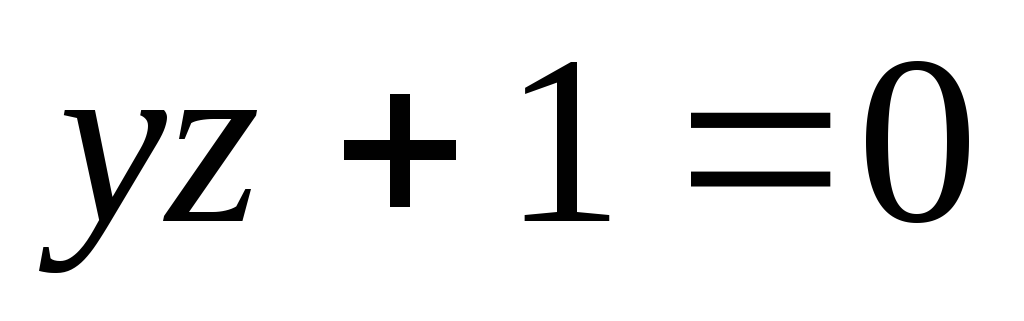Экзаменатор_________________
ГОУ ВПО
«Брянский государственный университет
имени академика И.Г.Петровского»
УТВЕРЖДАЮ:
Зав. кафедрой____________________
« » 2011 года Курс 2, ИТ, ФМФ
Экзаменационный билет № 5
по дифференциальным и разностным уравнениям
Уравнения параболического типа. Решение задачи Коши для уравнения теплопроводности методом разделения переменных. Интеграл Пуассона и фундаментальное решение.
Дифференциальная форма ДУ. Уравнения с разделенными переменными.
Найти общее решение уравнения
.
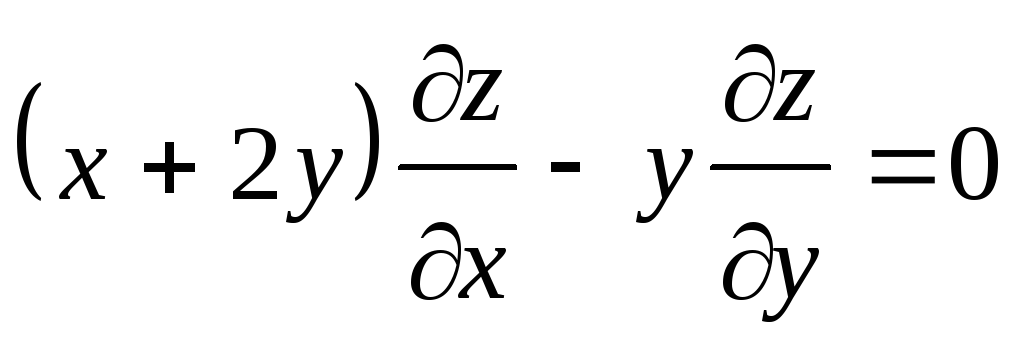Экзаменатор_________________
ГОУ ВПО
«Брянский государственный университет
имени академика И.Г.Петровского»
УТВЕРЖДАЮ:
Зав. кафедрой____________________
« » 2011 года Курс 2, ИТ, ФМФ
Экзаменационный билет № 6
по дифференциальным и разностным уравнениям
Уравнения с разделяющимися переменными.
Уравнения эллиптического типа. Гармонические функции. Постановка краевых задач.
Привести к каноническому виду уравнение
.
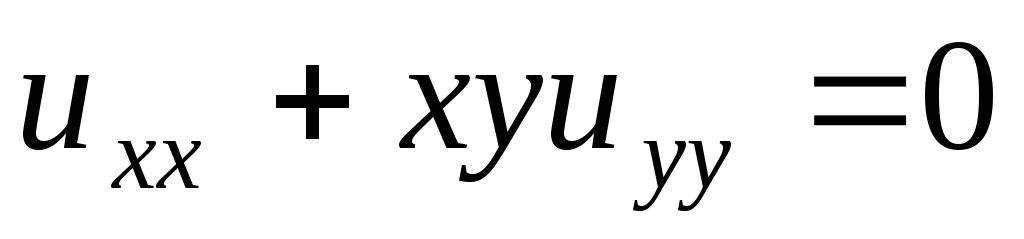Экзаменатор_________________
ГОУ ВПО
«Брянский государственный университет
имени академика И.Г.Петровского»
УТВЕРЖДАЮ:
Зав. кафедрой____________________
« » 2011 года Курс 2, ИТ, ФМФ
Экзаменационный билет № 7
по дифференциальным и разностным уравнениям
Однородные уравнения.
Классификация дифференциальных уравнений в частных производных второго порядка. Примеры. Типы краевых задач для дифференциальных уравнений.
Найти общее решение или общий интеграл уравнения
.
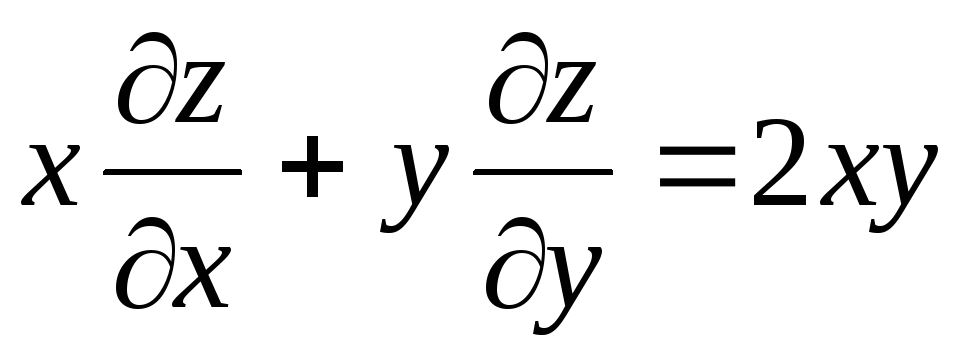Экзаменатор________________
ГОУ ВПО
«Брянский государственный университет
имени академика И.Г.Петровского»
УТВЕРЖДАЮ:
Зав. кафедрой____________________
« » 2011 года Курс 2, ИТ, ФМФ
Экзаменационный билет № 8
по дифференциальным и разностным уравнениям
Уравнения параболического типа. Каноническая форма.
Уравнения, сводящиеся к уравнениям в полных дифференциалах. Интегрирующий множитель. Частные случаи нахождения интегрирующего множителя.
Решить дифференциальное уравнение
.
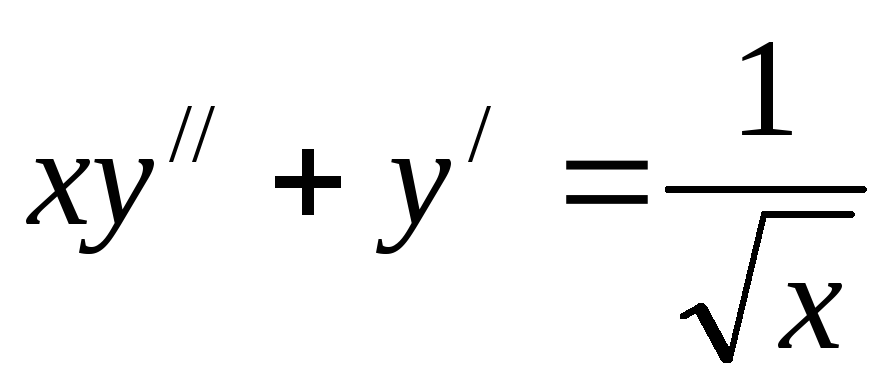Экзаменатор_________________
ГОУ ВПО
«Брянский государственный университет
имени академика И.Г.Петровского»
УТВЕРЖДАЮ:
Зав. кафедрой____________________
« » 2011 года Курс 2, ИТ, ФМФ
Экзаменационный билет № 9
по дифференциальным и разностным уравнениям
Понятие дифференциального уравнения п-го порядка.
Уравнения гиперболического типа. Применение метода Фурье разделения переменных к решению задачи о вынужденных колебаниях однородной струны с подвижными концами. Обоснование метода в случае неоднородного уравнения.
Решить задачу Коши
.
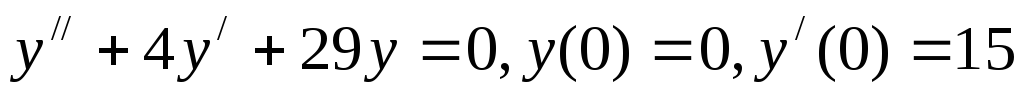Экзаменатор_________________
ГОУ ВПО
«Брянский государственный университет
имени академика И.Г.Петровского»
УТВЕРЖДАЮ:
Зав. кафедрой____________________
« » 2011 года Курс 2, ИТ, ФМФ
Экзаменационный билет № 10
по дифференциальным и разностным уравнениям
Задача Коши. Теорема Пикара.
Уравнения параболического типа. Решение задачи Коши для уравнения теплопроводности методом разделения переменных. Интеграл Пуассона и фундаментальное решение.
Решить дифференциальное уравнение
.
Экзаменатор_________________
ГОУ ВПО
«Брянский государственный университет
имени академика И.Г.Петровского»
УТВЕРЖДАЮ:
Зав. кафедрой____________________
« » 2011 года Курс 2, ИТ, ФМФ
Экзаменационный билет № 11
по дифференциальным и разностным уравнениям
Линейные дифференциальные уравнения п-го порядка. Однородные и неоднородные уравнения.
Уравнения гиперболического типа. Применение метода Фурье разделения переменных к решению задачи о вынужденных колебаниях однородной струны с подвижными концами.
Однородная струна, закрепленная на концах
,
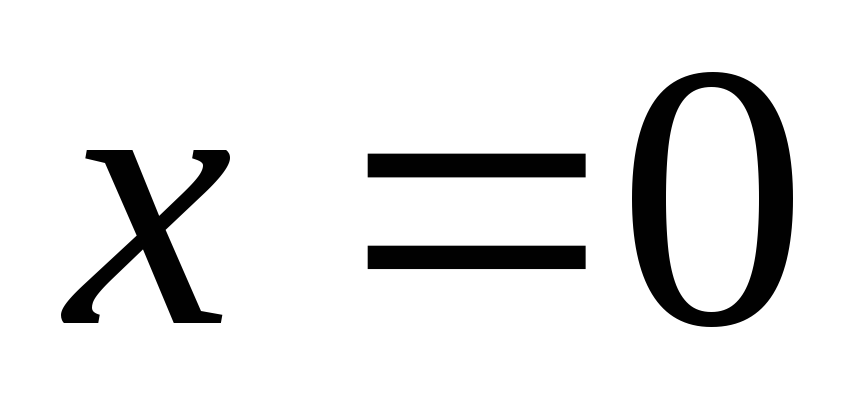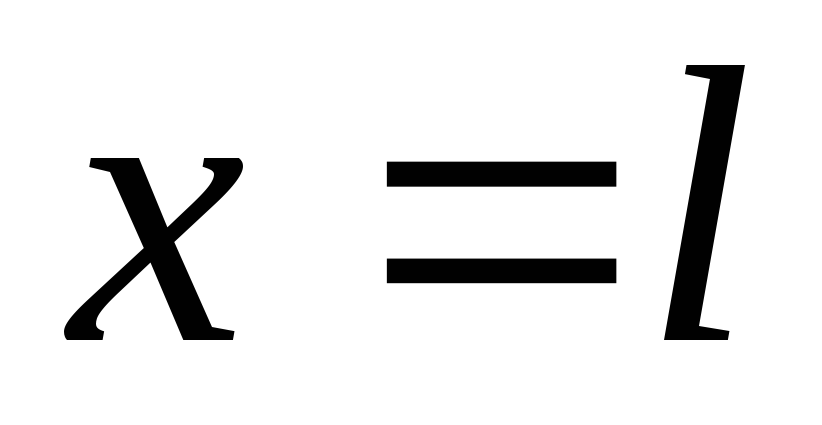и имеющая в начальный момент времени
форму
,
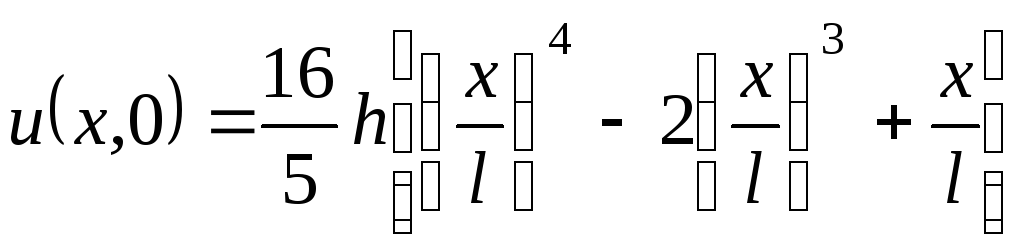где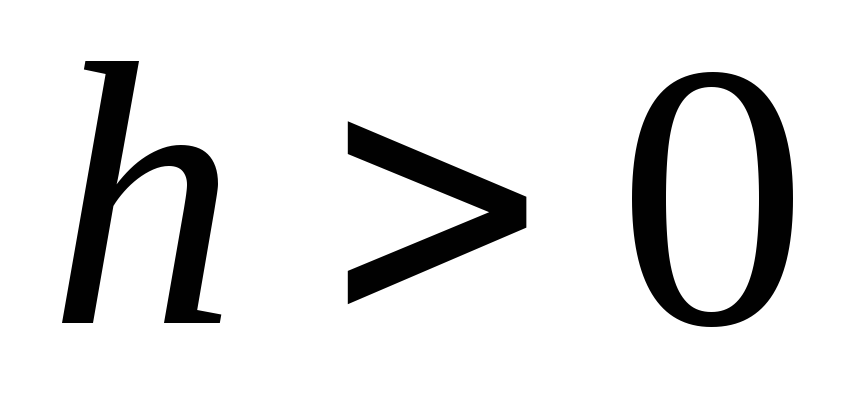
- достаточно малое число, начала
колебаться без начальной скорости.
Найти свободные колебания струны.
Экзаменатор_________________
ГОУ ВПО
«Брянский государственный университет
имени академика И.Г.Петровского»
УТВЕРЖДАЮ:
Зав. кафедрой____________________
« » 2011 года Курс 2, ИТ, ФМФ
Экзаменационный билет № 12
по дифференциальным и разностным уравнениям
Линейный дифференциальный оператор п-го порядка, его свойства.
Уравнения гиперболического типа. Решение задачи Коши для неограниченной струны. Формула Даламбера.
Найти распределение температуры в стержне длиной l, если на концах его поддерживается температура, равная нулю, а начальная температура равна единице вдоль всего стержня.
Экзаменатор_________________
Брянский государственный университет
имени академика И.Г.Петровского
УТВЕРЖДАЮ:
Зав. кафедрой____________________
“ “ 2008 года Курс 4
Экзаменационный билет № 13
по уравнениям математической физики
Уравнения гиперболического типа. Канонический вид.
Уравнения параболического типа. Решение задачи Коши для уравнения теплопроводности методом разделения переменных. Интеграл Пуассона и фундаментальное решение.
Однородная струна, закрепленная на концах
,
,
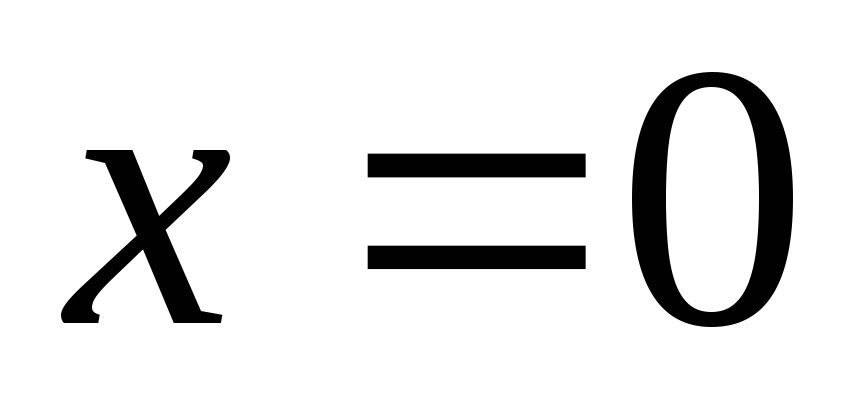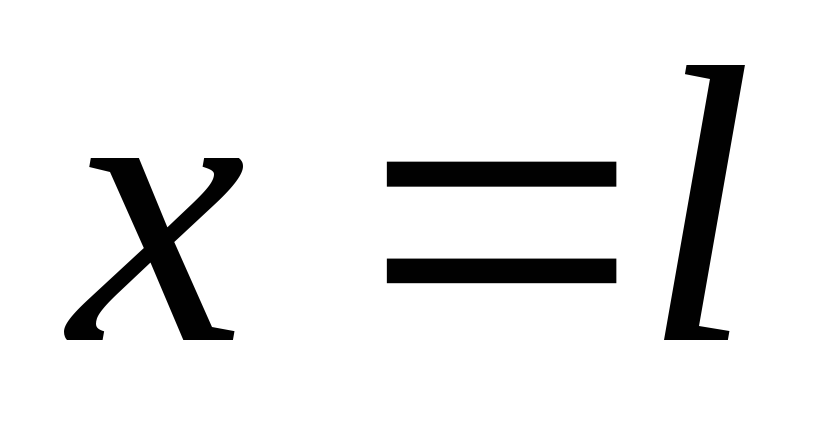имеет в начальный момент времени форму
параболы, симметричной относительно
перпендикуляра, проведенного через
точку
.
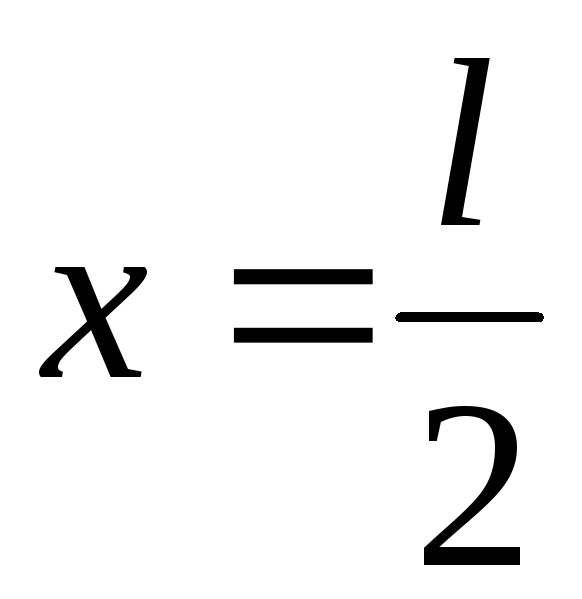Определить смещение точек струны от
прямолинейного положения равновесия,
предполагая, что начальные скорости
отсутствуют.