
Госы 5к Надя / уравнения математической физики / Модуль 2 / лекции / 3-4
.docУравнения в частных производных второго порядка Лекция №3-4
Тема: Уравнения в частных производных второго порядка.
Вопросы:
1. Общий вид уравнения второго порядка. Линейные уравнения второго порядка в частных производных. Линейные однородные и линейные неоднородные уравнения.
2. Свойства решений линейного однородного и линейного неоднородного уравнений.
3. Классификация дифференциальных уравнений второго порядка.
4. Приведение линейного уравнения к каноническому виду: гиперболический тип, параболический тип и эллиптический тип.
5. Постановка основных задач для линейных дифференциальных уравнений второго порядка.
Уравнение вида
![]() (3.1)
(3.1)
есть дифференциальное уравнение второго порядка с искомой функцией z от двух переменных х и у.
Уравнения математической физики в отличие от уравнений с частными производными второго порядка общего вида (3.1) являются линейными, т.е. линейно зависят от искомой функции и ее частных производных. Например, в случае двух независимых переменных они имеют вид
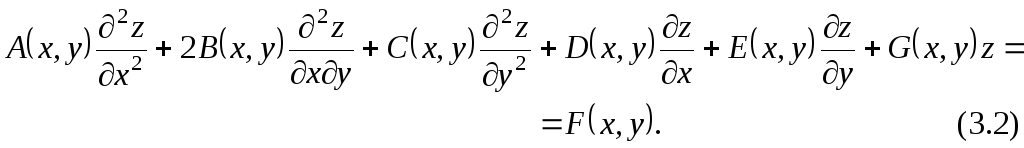
Уравнение (3.2)
называется однородным, если
![]() .
Если
.
Если
![]() ,
то уравнение (3.2) называется неоднородным.
,
то уравнение (3.2) называется неоднородным.
Обозначим левую
часть уравнения (3.2) через
![]() ,
тогда (3.2) можно записать в виде:
,
тогда (3.2) можно записать в виде:
![]() . (3.3)
. (3.3)
Соответствующее однородное уравнение примет вид
![]() . (3.4)
. (3.4)
![]() - линейный
дифференциальный оператор. Самостоятельно
проверить свойства линейности оператора
- линейный
дифференциальный оператор. Самостоятельно
проверить свойства линейности оператора
![]() .
.
Из свойств линейности
оператора
![]() непосредственно вытекают следующие
утверждения:
непосредственно вытекают следующие
утверждения:
Теорема 3.1.
Если
![]() - решение линейного однородного уравнения
(3.4), то функция
- решение линейного однородного уравнения
(3.4), то функция
![]() также является решением уравнения
(3.4), где С
– произвольная постоянная.
также является решением уравнения
(3.4), где С
– произвольная постоянная.
Теорема 3.2.
Если
![]() и
и
![]() - решения линейного однородного уравнения
(3.4), то сумма
- решения линейного однородного уравнения
(3.4), то сумма
![]() +
+
![]() также является решением этого уравнения.
также является решением этого уравнения.
Следствие.
Линейная комбинация с произвольными
постоянными коэффициентами k
решений уравнения (3.4)
![]() также является решением этого уравнения.
также является решением этого уравнения.
В отличие от обыкновенных линейных однородных дифференциальных уравнений, имеющих конечное число линейно независимых частных решений, линейная комбинация которых дает общее решение этого уравнения, уравнения в частных производных могут иметь бесконечное множество линейно независимых частных решений.
Например. Уравнение
![]()
имеет общее решение
![]() ,
поэтому его решениями будут, например,
функции
,
поэтому его решениями будут, например,
функции
![]() .
.
Для линейного неоднородного
![]() . (3.5)
. (3.5)
уравнения справедливы следующие утверждения:
Теорема 3.3.
Если
![]() - решение линейного неоднородного
уравнения (3.5), а
- решение линейного неоднородного
уравнения (3.5), а
![]() - решение соответствующего однородного
уравнения (3.4), сумма
- решение соответствующего однородного
уравнения (3.4), сумма
![]() также является решением неоднородного
уравнения (3.5).
также является решением неоднородного
уравнения (3.5).
Теорема 3.4.
Если
![]() - решение уравнения
- решение уравнения
![]() ,
а
,
а
![]() - решения уравнения
- решения уравнения
![]() ,
то сумма
,
то сумма
![]() +
+
![]() является решением уравнения
является решением уравнения
![]() .
.
Рассмотрим классификацию дифференциальных уравнений второго порядка с двумя независимыми переменными.
Определение.
Линейное дифференциальное уравнение
второго порядка (3.2) в некоторой области
![]() на плоскости хОу
называется
на плоскости хОу
называется
-
гиперболическим в
 ,
если
,
если
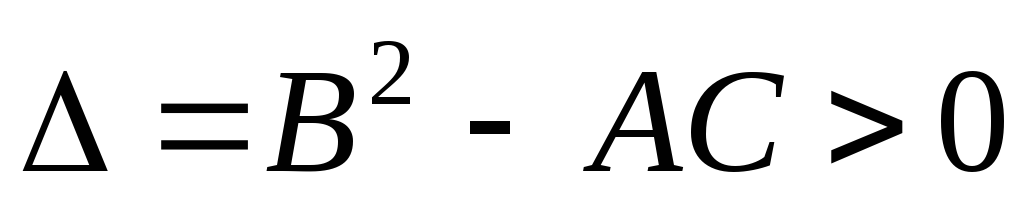 в
в
 ;
; -
эллиптическим в
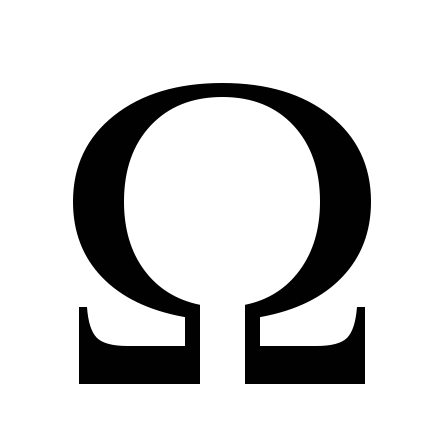 , если
, если
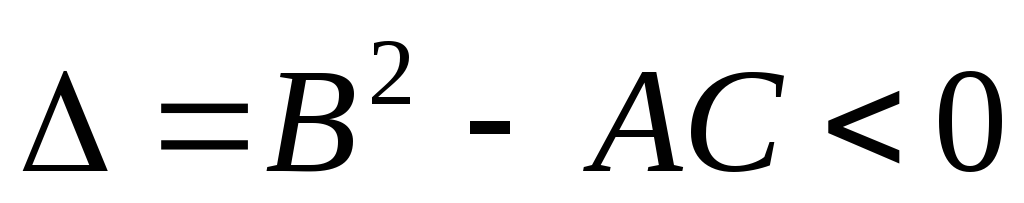 в
в
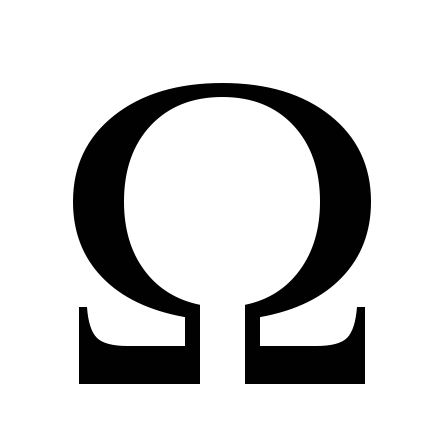 ;
; -
параболическим в
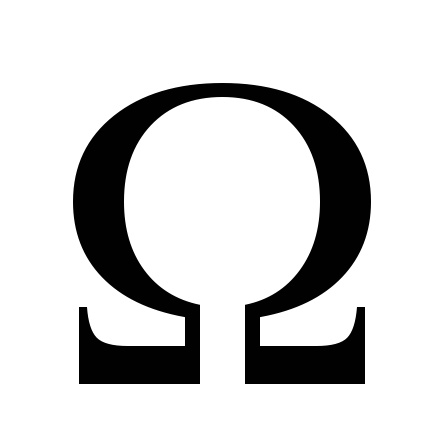 , если
, если
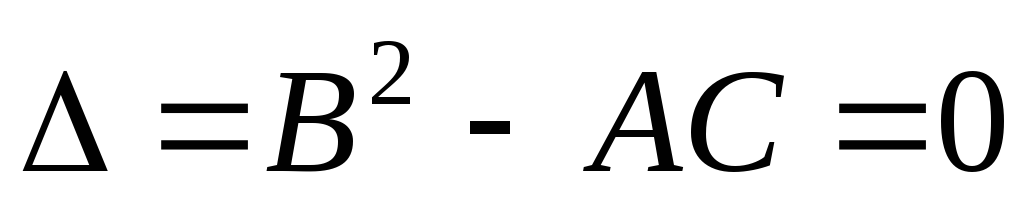 в
в
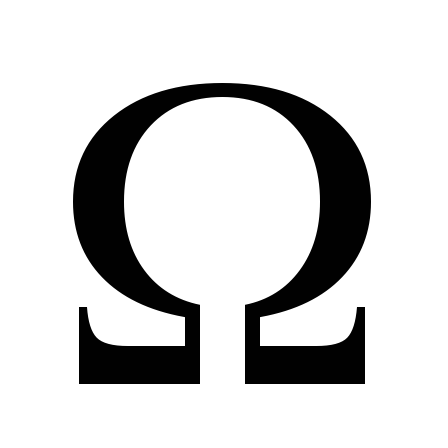 .
.
Простейшим из уравнений гиперболического типа является волновое уравнение
![]() .
.
Оно встречается в задачах, связанных с колебательными процессами.
Простейшим из уравнений эллиптического типа является уравнение Лапласа
![]() .
.
К интегрированию этого уравнения приходят при изучении стационарных процессов.
Простейшим уравнением параболического типа является уравнение теплопроводности (уравнение Фурье)
![]() .
.
Оно часто встречается при изучении процессов теплопроводности и диффузии.
Позже мы с вами рассмотрим эти уравнения подробнее.
В курсе математической физики также изучаются волновое уравнение, уравнение Лапласа и уравнение Фурье более общего вида:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Приведем уравнение
(3.2) к каноническому виду в достаточно
малой окрестности любой точки, в которой
задано это уравнение. Предположим, что
коэффициенты А,
В
и С
в уравнении (3.2) принадлежат классу
![]() в некоторой окрестности и нигде в ней
не обращаются в нуль одновременно. Для
определенности можно считать, что
в некоторой окрестности и нигде в ней
не обращаются в нуль одновременно. Для
определенности можно считать, что
![]() в этой окрестности. Действительно, в
противном случае может оказаться, что
в этой окрестности. Действительно, в
противном случае может оказаться, что
![]() ,
но тогда меняя местами х
и у,
получим уравнение у которого
,
но тогда меняя местами х
и у,
получим уравнение у которого
![]() .
Если же А
и С
обращаются одновременно в нуль в
какой-нибудь точке, то
.
Если же А
и С
обращаются одновременно в нуль в
какой-нибудь точке, то
![]() в окрестности этой точки. В таком случае
после деления на 2В
уравнение (3.2) уже будет иметь канонический
вид:
в окрестности этой точки. В таком случае
после деления на 2В
уравнение (3.2) уже будет иметь канонический
вид:
![]() .
.
Перейдем теперь к новым переменным
![]() ,
,
![]()
![]() ,
,
![]() , (3.6)
, (3.6)
тогда
![]() ,
,
![]() ,
,
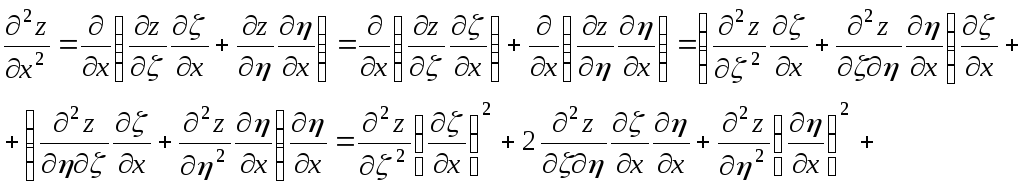
![]() ,
,

![]() ,
,
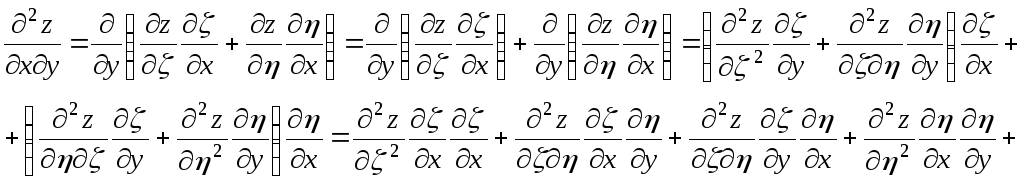
![]() .
.
Поэтому уравнение (3.2) примет вид
![]() , (*)
, (*)
где
![]() ,
,
![]() ,
,
![]() .
.
Потребуем, чтобы
функции
![]() и
и
![]() обращали в нуль коэффициенты
обращали в нуль коэффициенты
![]() и
и
![]() ,
т.е. удовлетворяли уравнениям:
,
т.е. удовлетворяли уравнениям:
![]() ,
,
![]() .
.
Так как
![]() ,
то эти уравнения эквивалентны линейным
уравнениям
,
то эти уравнения эквивалентны линейным
уравнениям
![]() ,
,
![]() , (3.7)
, (3.7)
где
![]() ,
,
![]() ,
,
![]() .
.
Как мы с вами
заметили, в зависимости от
![]() возможны три типа уравнений. Рассмотрим
отдельно эти три случая.
возможны три типа уравнений. Рассмотрим
отдельно эти три случая.
-
Гиперболический тип,
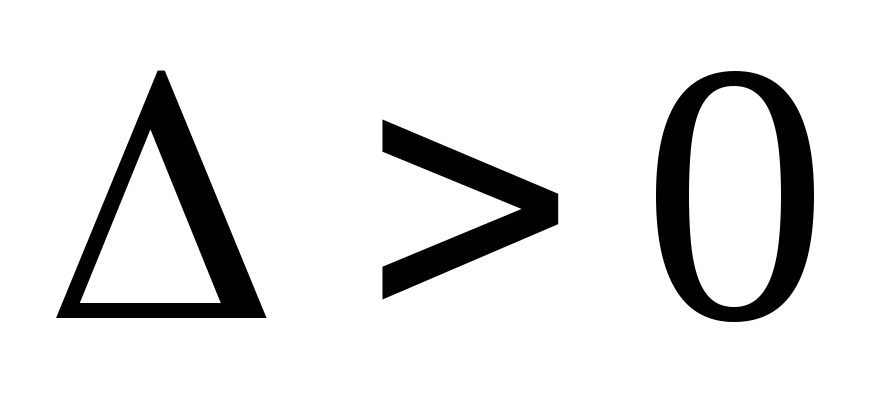 .
.
В этом случае уравнение (3.2) приводится к каноническому виду:
![]() . (3.8)
. (3.8)
Замена переменных
![]() ,
,
![]() приводит уравнение (3.2) к другому,
эквивалентному, каноническому виду:
приводит уравнение (3.2) к другому,
эквивалентному, каноническому виду:
![]() . (3.9)
. (3.9)
Для доказательства
представления (3.8) покажем, что существует,
по крайней мере, одна пара решений
![]() и
и
![]() уравнений (3.7), удовлетворяющих условиям
(3.6). Установим сначала связь этих решений
с характеристиками уравнения (3.2).
уравнений (3.7), удовлетворяющих условиям
(3.6). Установим сначала связь этих решений
с характеристиками уравнения (3.2).
Предположим, что
существуют решения уравнений (3.7), такие
что
![]() ,
,
![]() в рассматриваемой окрестности, тогда
кривые
в рассматриваемой окрестности, тогда
кривые
![]() ,
,
![]()
определяют два семейства характеристик уравнения (3.2). Докажем теперь следующее вспомогательное утверждение.
Лемма.
Пусть функция
![]() такая, что
такая, что
![]() .
Для того, чтобы семейство кривых
.
Для того, чтобы семейство кривых
![]() определяло характеристики уравнения
(3.2), необходимо и достаточно, чтобы
выражение
определяло характеристики уравнения
(3.2), необходимо и достаточно, чтобы
выражение
![]() было общим интегралом одного из
обыкновенных дифференциальных уравнений
было общим интегралом одного из
обыкновенных дифференциальных уравнений
![]() ,
,
![]() . (3.10)
. (3.10)
Уравнения (3.10) называются дифференциальными уравнениями характеристик уравнения (3.2).
Доказательство.
1. Докажем необходимость. Пусть
![]() - семейство характеристик уравнения
(3.2). Из условия
- семейство характеристик уравнения
(3.2). Из условия
![]() следует, что данное семейство заполняет
некоторую окрестность D,
через каждую точку которой проходит
одна и только одна характеристика. Пусть
следует, что данное семейство заполняет
некоторую окрестность D,
через каждую точку которой проходит
одна и только одна характеристика. Пусть
![]() .
Тогда, если в преобразовании (3.6) взять,
например,
.
Тогда, если в преобразовании (3.6) взять,
например,
![]() ,
то в этой окрестности функция
,
то в этой окрестности функция
![]() будет удовлетворять уравнению
будет удовлетворять уравнению
![]() .
.
Так как на каждой характеристике справедливо соотношение
![]() ,
,
![]() ,
,
![]() ,
,
то поскольку
![]() ,
получаем
,
получаем
![]() ,
или
,
или
![]() ,
,
т.е.
![]() есть общий интеграл первого из уравнений
(3.10). Необходимость доказана.
есть общий интеграл первого из уравнений
(3.10). Необходимость доказана.
2. Докажем
достаточность. Пусть
![]() есть общий интеграл одного из уравнений
(3.10), например, первого из них. По
определению это значит, что если функция
есть общий интеграл одного из уравнений
(3.10), например, первого из них. По
определению это значит, что если функция
![]() является решением этого уравнения, то
является решением этого уравнения, то
![]() ,
,
поэтому, продифференцировав последнее тождество по х, будем иметь
![]() ,
,
и, следовательно,
на каждой линии
![]() выполняется соотношение
выполняется соотношение
![]() . (3.11)
. (3.11)
Но по теореме
существования и единственности решения
для обыкновенных дифференциальных
уравнений через каждую точку из
рассматриваемой окрестности проходит
одна интегральная кривая
![]() этого уравнения. Поэтому уравнение
(3.11) выполняется во всех точках
рассматриваемой окрестности. А так как
по условию
этого уравнения. Поэтому уравнение
(3.11) выполняется во всех точках
рассматриваемой окрестности. А так как
по условию
![]() ,
,
![]() ,
то кривые
,
то кривые
![]() являются характеристиками уравнения
(3.2). Лемма доказана.
являются характеристиками уравнения
(3.2). Лемма доказана.
На основании доказанной леммы общие интегралы уравнений (3.10):
![]() ,
и
,
и
![]()
такие, что
![]() ,
,
![]() ,
,
![]() ,
определяют два семейства характеристик
уравнения (3.2). Причем, так как
,
определяют два семейства характеристик
уравнения (3.2). Причем, так как
![]() ,
то и
,
то и
![]() ,
а так же
,
а так же
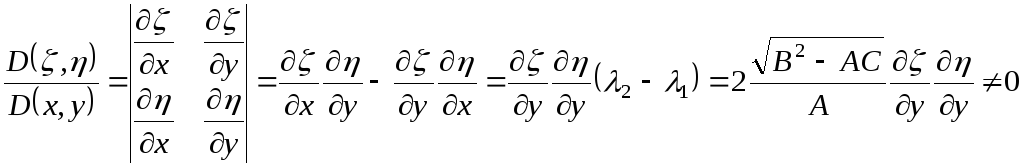 .
.
Т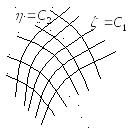 аким
образом, семейства характеристик
аким
образом, семейства характеристик
![]() ,
,
![]() образуют семейства координатных линий
и функции
образуют семейства координатных линий
и функции
![]() и
и
![]() можно принять за новые переменные. При
этом в уравнении (*) коэффициенты
можно принять за новые переменные. При
этом в уравнении (*) коэффициенты
![]() и
и
![]() будут равны нулю и
будут равны нулю и
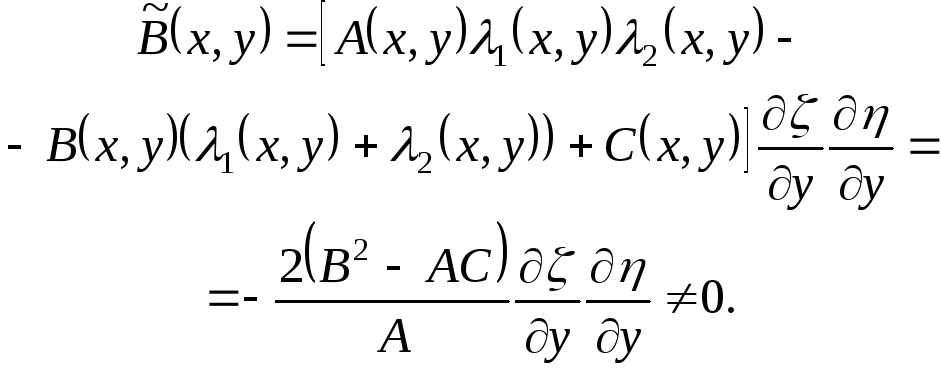
Поэтому, разделив
уравнение (*) на 2![]() ,
получим уравнение в канонической форме
(3.8).
,
получим уравнение в канонической форме
(3.8).
-
Параболический тип,
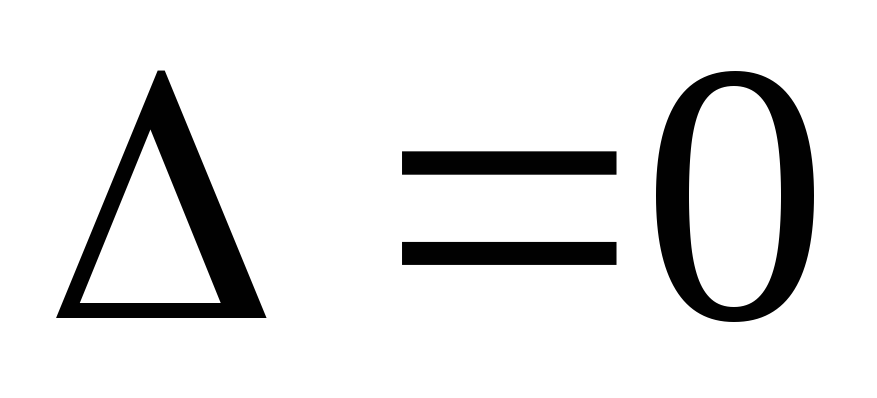 .
.
Уравнение (3.2) приводится к каноническому виду
![]() .
.
Так как в некоторой
окрестности
![]() ,
то
,
то
![]() ,
поэтому дифференциальные уравнения
(3.7) совпадают и равны
,
поэтому дифференциальные уравнения
(3.7) совпадают и равны
![]() .
.
Следовательно, мы
получили одно семейство характеристик
![]() уравнения (3.2), определяемое в силу леммы,
общим интегралом уравнения
уравнения (3.2), определяемое в силу леммы,
общим интегралом уравнения
![]() ,
,
таким что
![]() и
и
![]() .
В качестве второго семейства координатных
линий выберем прямые
.
В качестве второго семейства координатных
линий выберем прямые
![]() .
В результате замена переменных
.
В результате замена переменных
![]() ,
,
![]() ,
,
![]()
дает
![]() ,
,
![]() ,
,
![]() .
.
Разделив уравнение
(*) на коэффициент
![]() ,
получим уравнение в канонической форме.
,
получим уравнение в канонической форме.
-
Эллиптический тип,
 .
.
Если коэффициенты А, В и С в уравнении (3.2) – аналитические функции в окрестности некоторой точки. Тогда это уравнение приводится к каноническому виду
![]() .
.
В этом случае,
коэффициенты
![]() и
и
![]() уравнений (3.7) – аналитические функции,
причем при действительных
уравнений (3.7) – аналитические функции,
причем при действительных
![]() :
:
![]() .
Из теоремы Ковалевской следует, что в
достаточно малой окрестности существует
аналитическое решение
.
Из теоремы Ковалевской следует, что в
достаточно малой окрестности существует
аналитическое решение
![]() уравнения
уравнения
![]() ,
,
удовлетворяющее
условию
![]() .
Положим теперь
.
Положим теперь
![]() ,
,
![]() , (3.12)
, (3.12)
где
![]() - функция, комплексно сопряженная с
- функция, комплексно сопряженная с
![]() .
Функция
.
Функция
![]() удовлетворяет второму уравнению из
(3.7):
удовлетворяет второму уравнению из
(3.7):
![]() ,
,
так как
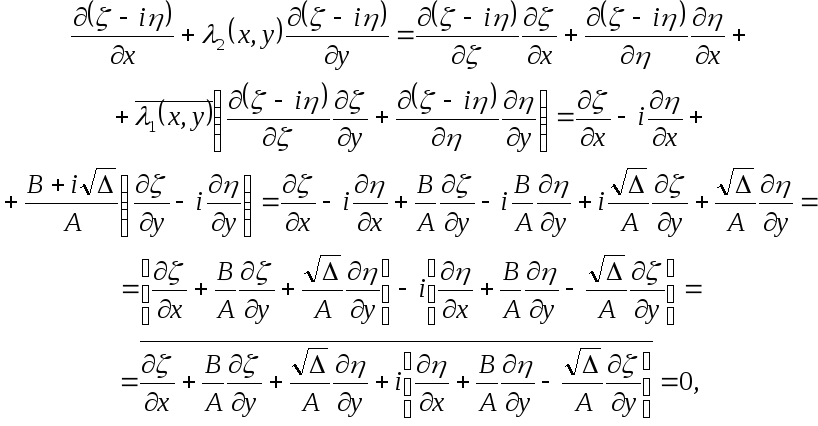
поскольку функция
![]() удовлетворяет первому уравнения из
(3.7), т.е.
удовлетворяет первому уравнения из
(3.7), т.е.

Так как функции
![]() и
и
![]() аналитические, то
аналитические, то
![]() и их якобиан
и их якобиан
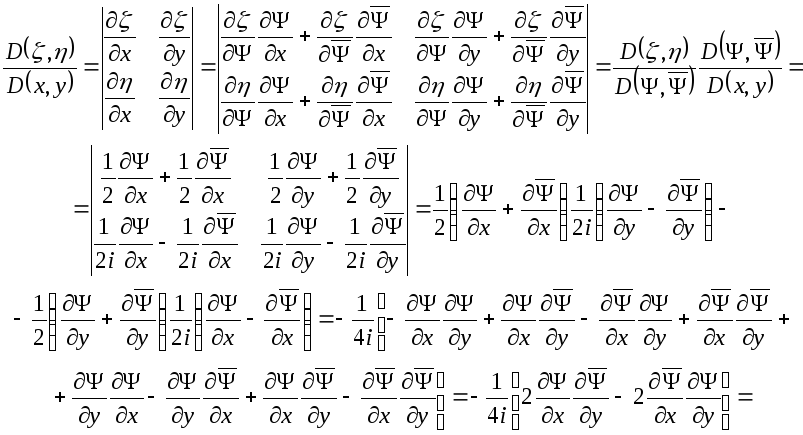
![]()
![]()
![]()
Поэтому функции
![]() и
и
![]() можно взять за новые переменные. По
построению функция
можно взять за новые переменные. По
построению функция
![]() удовлетворяет уравнению
удовлетворяет уравнению
![]() .
.
Выделим действительную и мнимую части и переходя к новым переменным пользуясь формулами (3.12), получим
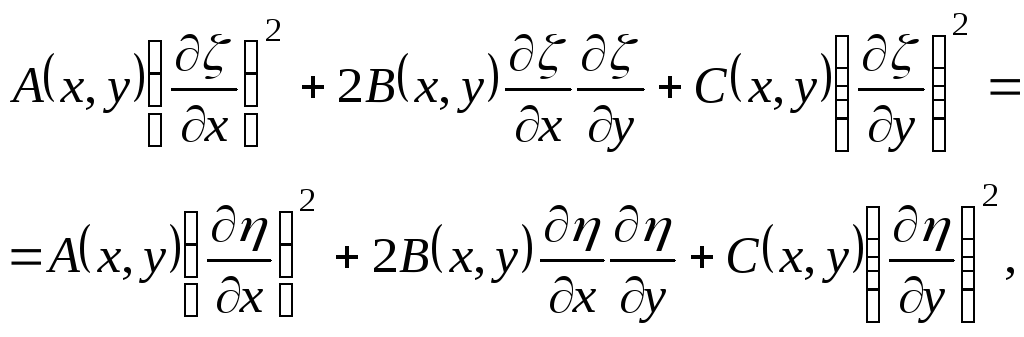 ,
,
![]() .
.
Учитывая формулы
для коэффициентов
![]() получаем, что
получаем, что
![]() и
и
![]() в переменных
в переменных
![]() и
и
![]() .
Далее, поскольку
.
Далее, поскольку
![]() и
и
![]() ,
то
,
то
![]() .
Разделив уравнение (*) на
.
Разделив уравнение (*) на
![]() ,
приведем его к каноническому виду
,
приведем его к каноническому виду
![]() .
.
Постановка основных задач для линейных дифференциальных уравнений второго порядка.
Чтобы полностью
описать тот или иной физический процесс,
необходимо кроме самого уравнения,
описывающего этот процесс, задать
начальное состояние этого процесса
(начальные условия) и режим на границе
той области
![]() ,
в которой происходит этот процесс
(граничные условия). Это связано с
неединственностью решения дифференциальных
уравнений. Так, например, для уравнений
в частных производных решение зависит
от произвольных функций. Поэтому, чтобы
выделить решение, описывающее реальный
физический процесс, необходимо задать
дополнительные условия. Такими
дополнительными условиями и являются
краевые условия (начальные и граничные).
Соответствующая задача называется
краевой задачей.
,
в которой происходит этот процесс
(граничные условия). Это связано с
неединственностью решения дифференциальных
уравнений. Так, например, для уравнений
в частных производных решение зависит
от произвольных функций. Поэтому, чтобы
выделить решение, описывающее реальный
физический процесс, необходимо задать
дополнительные условия. Такими
дополнительными условиями и являются
краевые условия (начальные и граничные).
Соответствующая задача называется
краевой задачей.
Выделяют три основных типа краевых задач для дифференциальных уравнений:
-
задача Коши для уравнений гиперболического и параболического типов. Задаются начальные условия, область
 совпадает со всем пространством
совпадает со всем пространством
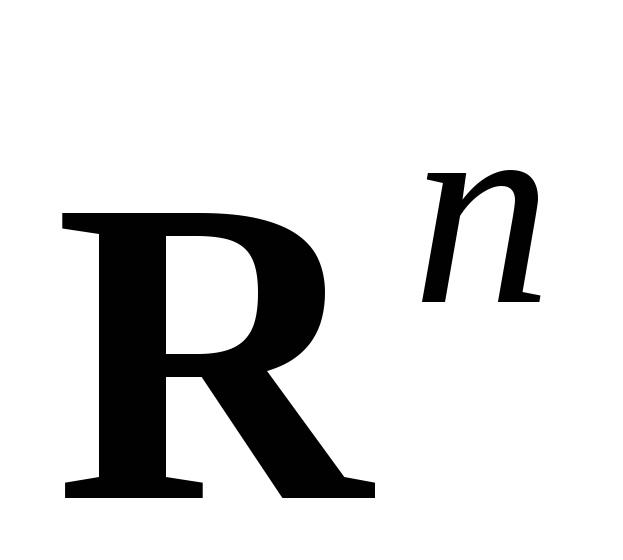 (п
– число независимых переменных),
граничные условия отсутствуют;
(п
– число независимых переменных),
граничные условия отсутствуют; -
краевая задача для уравнений эллиптического типа. Задаются граничные условия на границе области
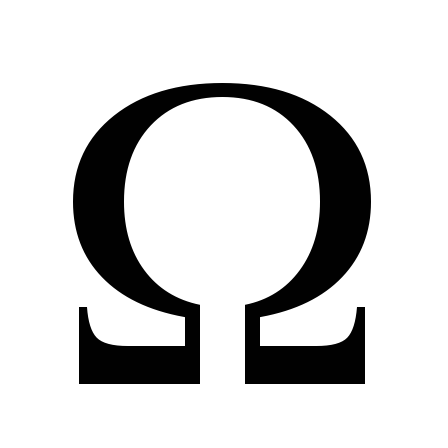 ,
начальные условия отсутствуют;
,
начальные условия отсутствуют; -
смешанная задача для уравнений гиперболического и параболического типов. Задаются и начальные и граничные условия,
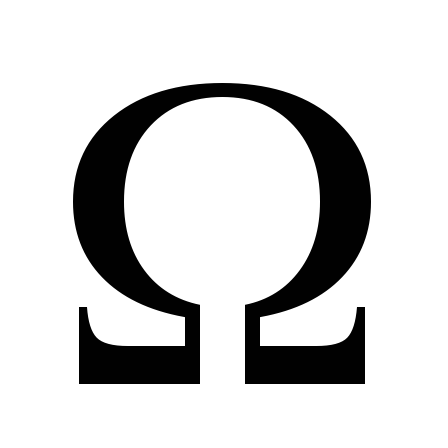

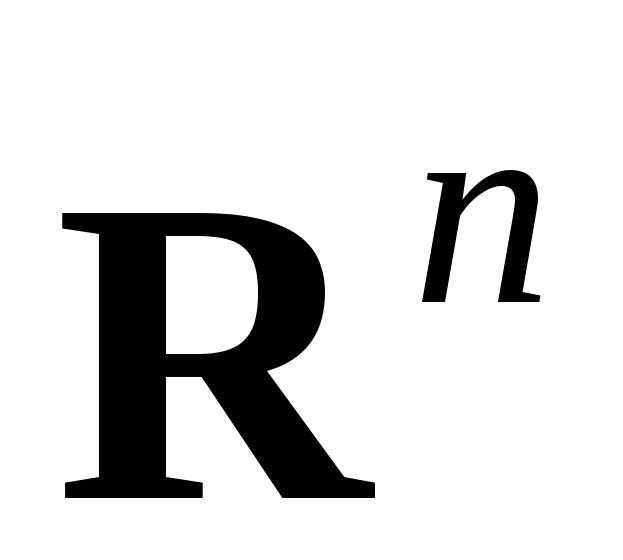 .
.
