
Госы 5к Надя / уравнения математической физики / Модуль 2 / лекции / 13
.docГармонические функции и их свойства Лекция №13
Тема: Гармонические функции и их свойства
Вопросы:
1. Фундаментальное решение уравнения Лапласа в пространстве и на плоскости.
2. Свойства гармонических функций: принцип максимума, теорема о среднем, теорема обратная к теореме о среднем, неравенство Харнака, теорема Лиувилля.
Рассмотрим уравнение Лапласа на плоскости
![]() (10.1)
(10.1)
и в пространстве
![]() (10.2)
(10.2)
Функции
![]() на плоскости и
на плоскости и
![]() в пространстве, имеющие непрерывные
частные производные второго порядка и
удовлетворяющие, соответственно,
уравнению Лапласа (10.1) или (10.2) в некоторой
области D,
называются гармоническими
в этой области. Простейшими примерами
гармонических функций являются линейные
функции:
в пространстве, имеющие непрерывные
частные производные второго порядка и
удовлетворяющие, соответственно,
уравнению Лапласа (10.1) или (10.2) в некоторой
области D,
называются гармоническими
в этой области. Простейшими примерами
гармонических функций являются линейные
функции:
![]() на плоскости и
на плоскости и
![]() в пространстве. Особый интерес представляют
решения уравнения Лапласа, обладающие
сферической или цилиндрической (в случае
двух независимых переменных - круговой)
симметрией, т.е. зависящие только от
одной переменной r.
в пространстве. Особый интерес представляют
решения уравнения Лапласа, обладающие
сферической или цилиндрической (в случае
двух независимых переменных - круговой)
симметрией, т.е. зависящие только от
одной переменной r.
Напомним, что уравнение Лапласа в цилиндрических координатах имеет вид (доказать самостоятельно)
![]() ;
;
в сферических (получить самостоятельно)
![]() .
.
Решение
![]() ,
обладающее сферической симметрией,
будет определяться из обыкновенного
дифференциального уравнения
,
обладающее сферической симметрией,
будет определяться из обыкновенного
дифференциального уравнения
![]() ,
,
![]() .
.
Это уравнение получится, если подставить искомую функцию в уравнение Лапласа (10.2), записанное в сферических координатах. Интегрируя это уравнение, находим
![]() ,
,
где C1
и C2
- произвольные постоянные. Полагая C1=1,
C2=0,
получим функцию
![]() ,
которую часто называют фундаментальным
решением уравнения Лапласа в пространстве.
Функция
,
которую часто называют фундаментальным
решением уравнения Лапласа в пространстве.
Функция
![]() является гармонической всюду в
пространстве, кроме начала координат
0.
является гармонической всюду в
пространстве, кроме начала координат
0.
Аналогично, полагая
![]() и пользуясь уравнением Лапласа в
цилиндрических или полярных координатах,
найдем решения, обладающие цилиндрической
или круговой симметрией:
и пользуясь уравнением Лапласа в
цилиндрических или полярных координатах,
найдем решения, обладающие цилиндрической
или круговой симметрией:
![]()
![]() ,
где
,
где
![]() .
.
Выбирая С1=-1
и С2=0,
будем иметь функцию
![]() ,
которую называют фундаментальным
решением уравнения Лапласа на плоскости
(в случае двух независимых переменных).
Функция
,
которую называют фундаментальным
решением уравнения Лапласа на плоскости
(в случае двух независимых переменных).
Функция
![]() удовлетворяет уравнению Лапласа (10.1)
всюду на плоскости, кроме начала координат
0, где она обращается в бесконечность.
Фундаментальные решения уравнения
Лапласа имеют, помимо большого значения
в теории гармонических функций, важный
физический смысл.
удовлетворяет уравнению Лапласа (10.1)
всюду на плоскости, кроме начала координат
0, где она обращается в бесконечность.
Фундаментальные решения уравнения
Лапласа имеют, помимо большого значения
в теории гармонических функций, важный
физический смысл.
Рассмотрим в
пространстве электрическое поле,
образованное точечным зарядом величины
q
, помещенным в начало координат. Тогда
потенциал этого поля равен
![]() .
.
Аналогично, если
рассмотреть поле, создаваемое заряженной
прямой, то потенциал такого поля будет
равен
![]() ,
где q1
- линейная плотность заряда (то есть
заряд, рассчитанный на единицу длины).
,
где q1
- линейная плотность заряда (то есть
заряд, рассчитанный на единицу длины).
Изучим некоторые свойства гармонических функций.
Лемма 1.
Если функция
![]() непрерывна в круге
непрерывна в круге
![]() и гармонична в области
и гармонична в области
![]() ,
v
– любое направление, образующее острый
угол с внутренней нормалью в точке
,
v
– любое направление, образующее острый
угол с внутренней нормалью в точке
![]() окружности, в которой
окружности, в которой
![]() для всех точек круга и если в точке
для всех точек круга и если в точке
![]() существует производная
существует производная
![]() ,
то
,
то
![]() в этой точке.
в этой точке.
Теорема (принцип
максимума модуля).
Гармоническая в области G
функция
![]() не может ни в какой внутренней точке
области G
принимать значение, равное верхней или
нижней грани значений
не может ни в какой внутренней точке
области G
принимать значение, равное верхней или
нижней грани значений
![]() в G.
в G.
Д
 оказательство.
Докажем от противного. Допустим, что
оказательство.
Докажем от противного. Допустим, что
![]() принимает значение
принимает значение
![]() в области G.
Обозначим
в области G.
Обозначим
![]() .
Если некоторая точка из Е
окажется на границе области G,
то теорема доказана. Поэтому найдется
область
.
Если некоторая точка из Е
окажется на границе области G,
то теорема доказана. Поэтому найдется
область
![]() :
в
:
в
![]() содержатся некоторые точки из Е
и по крайней мере одна точка Р
содержатся некоторые точки из Е
и по крайней мере одна точка Р![]() такая, что
такая, что
![]() (здесь
(здесь
![]() ).
Это утверждение справедливо, так как в
).
Это утверждение справедливо, так как в
![]() существуют точки, сколь угодно близкие
к Е,
а для всех точек
существуют точки, сколь угодно близкие
к Е,
а для всех точек
![]() расстояние до границы G
больше некоторого положительного числа.
расстояние до границы G
больше некоторого положительного числа.
Рассмотрим круг
К
с радиусом
![]() и центром в точке Р.
Этот круг
и центром в точке Р.
Этот круг
![]() и все его внутренние точки не принадлежат
Е,
причем на окружности этого круга
обязательно найдется точка
и все его внутренние точки не принадлежат
Е,
причем на окружности этого круга
обязательно найдется точка
![]() .
Это следует из определения
.
Это следует из определения
![]() и из того, что предельные точки множества
Е,
содержащиеся в G,
принадлежат Е.
В точках множества Е
должно быть
и из того, что предельные точки множества
Е,
содержащиеся в G,
принадлежат Е.
В точках множества Е
должно быть
![]() .
Но так как хотя бы одна из координатных
осей не совпадает с касательной к границе
круга в точке Q,
то в силу леммы 1 хотя бы одна из производных
.
Но так как хотя бы одна из координатных
осей не совпадает с касательной к границе
круга в точке Q,
то в силу леммы 1 хотя бы одна из производных
![]() или
или
![]() должна быть > нуля. Полученное
противоречие показывает, что гармоническая
функция
должна быть > нуля. Полученное
противоречие показывает, что гармоническая
функция
![]() не может принимать внутри G
значение, равное m.
Так как
не может принимать внутри G
значение, равное m.
Так как
![]() ,
то теорема доказана полнлстью.
,
то теорема доказана полнлстью.
Теорема о среднем.
Пусть
![]() - гармоническая в некотором круге D
радиуса R
с центром (хo,уo)
и непрерывная в соответствующем замкнутом
круге
- гармоническая в некотором круге D
радиуса R
с центром (хo,уo)
и непрерывная в соответствующем замкнутом
круге
![]() функция. Тогда значение этой функции в
центре круга равно ее среднему
значению на окружности Г,
ограничивающей данный круг, то есть
функция. Тогда значение этой функции в
центре круга равно ее среднему
значению на окружности Г,
ограничивающей данный круг, то есть
![]() . (10.3)
. (10.3)
При доказательстве этой теоремы применим интегральную формулу Пуассона для круга, которая доказана в лекции 11-12. Она имеет вид (см. рис. 14)
![]() .
.
Если в этой формуле
положить
![]() ,
то получится формула (10.3).
,
то получится формула (10.3).
Теорему о среднем
можно представить и в другой форме. Для
этого запишем формулу (10.3) для произвольного
круга радиуса r,
где
![]() (см.
рис.15):
(см.
рис.15):
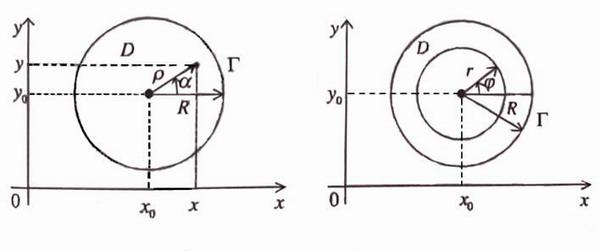
Рис. 14 Рис. 15
![]() . (10.14)
. (10.14)
Умножив обе части равенства (10.14) на rdr и проинтегрировав по r в пределах от 0 до R, получим:
![]() ,
,
или
![]() ,
где D
- круг радиуса R.
Разделив обе части полученного равенства
на R2/2
, будем иметь
,
где D
- круг радиуса R.
Разделив обе части полученного равенства
на R2/2
, будем иметь
![]() (10.15)
(10.15)
В правой части формулы (10.15) записано среднее значение гармонической функции U(x,y) в круге радиуса R.
Имеет место и
обратная теорема:
если в некоторой области D
функция
![]() непрерывная и для каждой точки
непрерывная и для каждой точки
![]() выполняется
теорема о среднем в любом сколь угодно
малом круге с центром в точке (хо,
уо),
то эта функция гармоническая в D.
выполняется
теорема о среднем в любом сколь угодно
малом круге с центром в точке (хо,
уо),
то эта функция гармоническая в D.
Из формулы (10.15) получается:
Следствие.
Если функция
![]() гармоническая в некотором круге D
радиуса R
и непрерывная в соответствующем замкнутом
круге
гармоническая в некотором круге D
радиуса R
и непрерывная в соответствующем замкнутом
круге
![]() ,то
,то
![]() . (10.16)
. (10.16)
Число
![]() называют нормой функции
называют нормой функции
![]() в области D,
и неравенство (10.16) можно переписать в
виде
в области D,
и неравенство (10.16) можно переписать в
виде
![]() .
.
Неравенство (10.16) доказывается совсем просто, если воспользоваться известным неравенством Коши-Буняковского:
![]()
Применим это неравенство к формуле (10.15):
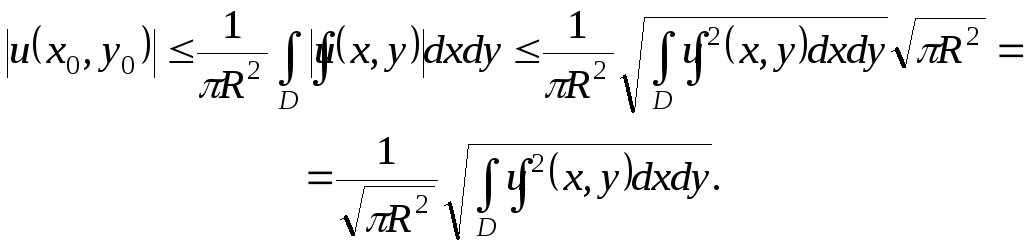
Что и требовалось доказать.
Гармонические функции, помимо вышеуказанных свойств, обладают и многими другими свойствами. Приведем еще два из них.
Неравенство
Харнака.
Пусть функция
![]() гармоническая в некотором круге D
радиуса R
c центром (xo,уo)
и непрерывная в соответствующем круге
гармоническая в некотором круге D
радиуса R
c центром (xo,уo)
и непрерывная в соответствующем круге
![]() .
Тогда при любом
.
Тогда при любом
![]() она
удовлетворяет неравенству
она
удовлетворяет неравенству
![]() .
.
Из неравенства Харнака следует теорема Лиувилля.
Теорема Лиувилля.
Гармоническая на всей плоскости функция
![]() не может быть ограниченной сверху или
снизу, если она не постоянная.
не может быть ограниченной сверху или
снизу, если она не постоянная.
Доказательство:
Если функция
![]() ограничена сверху, то
ограничена сверху, то
![]() - ограничена снизу и тоже гармоническая.
Поэтому достаточно рассмотреть случай,
когда функция ограничена снизу:
- ограничена снизу и тоже гармоническая.
Поэтому достаточно рассмотреть случай,
когда функция ограничена снизу:
![]() .
Более того, можно считать, что M=0.
Действительно,
.
Более того, можно считать, что M=0.
Действительно,
![]() ,а
разность
,а
разность
![]() тоже гармоническая функция. Итак,
предполагая существование гармонической
во всей плоскости неотрицательной
функции
тоже гармоническая функция. Итак,
предполагая существование гармонической
во всей плоскости неотрицательной
функции
![]() ,
мы докажем, что эта функция постоянная.
,
мы докажем, что эта функция постоянная.
Воспользуемся
неравенством Харнака
![]()
![]() .
.
Если функция
![]() гармоническая во всей плоскости
гармоническая во всей плоскости
![]() то,
зафиксировав произвольное
то,
зафиксировав произвольное
![]() и
неограниченно увеличивая R
и
неограниченно увеличивая R
![]() мы
получим
мы
получим
![]() ,
т.е.
,
т.е.
![]() .
Теорема доказана.
.
Теорема доказана.
Замечание. Гармонические функции в пространстве обладают аналогичными свойствами. Приведем формулировку одного из них.
Терема о среднем.
Пусть функция
![]() гармоническая в некотором шаре D
радиуса R
c центром
гармоническая в некотором шаре D
радиуса R
c центром
![]() и непрерывная в соответствующем замкнутом
шаре
и непрерывная в соответствующем замкнутом
шаре
![]() .
Тогда значение этой функции в центре
шара равно:
.
Тогда значение этой функции в центре
шара равно:
а) ее среднему значению на сфере Г, ограничивающей данный шар, то есть
![]() ;
;
б) ее среднему значению в шаре D, то есть
![]() .
.
Другие свойства гармонических функций в пространстве сформулировать самостоятельно.
