
Госы 5к Надя / уравнения математической физики / Модуль 2 / лекции / 6-7
.docМетод Фурье для уравнения колебаний струны Лекция №6-7
Тема: Метод Фурье.
Вопросы:
1. Задача о вынужденных колебаниях однородной струны. Сведение ее к задаче о колебаниях однородной струны с закрепленными концами.
2. Применение метода Фурье к решению задачи о свободных колебаниях однородной струны. Задача Штурма-Лиувиля, собственные значения и собственные функции.
3. Обоснование метода Фурье в случае неоднородного уравнения.
4. Колебания защепленной струны.
Метод Фурье или метод разделения переменных – один из наиболее распространенных методов решения уравнений в частных производных. Рассмотрим применение этого метода на примере задачи о вынужденных колебаниях однородной струны.
Задача о вынужденных колебаниях струны длины l с подвижными концами сводится к интегрированию уравнения
![]() ,
,
![]() ,
,
![]() , (5.1)
, (5.1)
при граничных условиях
![]() ,
,
![]()
![]() , (5.2)
, (5.2)
и начальных условиях
![]() ,
,
![]() ,
,
![]() . (5.3)
. (5.3)
При движении концов
сила натяжения однородной струны (![]() )
не должна меняться, так как
)
не должна меняться, так как
![]() .
.
Введением новой неизвестной функции
![]() ,
,
перейдем от задачи (5.1) – (5.3) к задаче с однородными граничными условиями:
![]() ,
,
![]() .
.
Подставляя
![]()
в уравнение, получим
новое уравнение относительно функции
![]()
![]() ,
,
причем
![]() ,
,
![]() .
.
Таким образом, без нарушения общности можно считать условия (5.2) однородными, т.е. концы струны закреплены. Эту задачу можно свести к двум:
![]() ,
,
![]() ,
,
![]() (5.4)
(5.4)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() , (5.5)
, (5.5)
![]() ,
,
![]() .
.
В дальнейшем
![]() и
и
![]() снова обозначим через и.
снова обозначим через и.
Задача (5.4) решается методом разделения переменных (методом Фурье), согласно которому решение ищется в виде
![]() , (5.6)
, (5.6)
Подставим это решение в исходное уравнение (5.4), получим
![]() ,
,
![]() ,
,
или, разделяя переменные,
![]() .
.
Это равенство
возможно только в том случае, когда его
обе части не зависят ни от х,
ни от t,
т.е. равны одной и той же постоянной,
обозначим ее через
![]() ,
тогда
,
тогда
![]() .
.
Получаем два обыкновенных дифференциальных уравнения
![]() ,
,
![]() .
.
Знак «минус» перед
![]() ставится только для удобства дальнейшей
записи. Это не означает, что константа
ставится только для удобства дальнейшей
записи. Это не означает, что константа
![]() отрицательна.
отрицательна.
Воспользуемся теперь граничными условиями, откуда
![]() ,
,
![]() ,
,
и так как
![]() ,
то функция Х
(х)
должна удовлетворять граничным условиям
,
то функция Х
(х)
должна удовлетворять граничным условиям
![]() ,
,
![]() .
.
Поэтому для того, чтобы найти нетривиальные решения вида (5.6), удовлетворяющие граничным условиям задачи (5.4), нужно найти нетривиальные решения уравнения
![]() , (5.7)
, (5.7)
удовлетворяющие граничным условиям
![]() ,
,
![]() . (5.8)
. (5.8)
Таким образом, нам
нужно найти значения параметра
![]() ,
при которых существуют нетривиальные
решения задачи (5.7) – (5.8), а также сами
эти решения.
,
при которых существуют нетривиальные
решения задачи (5.7) – (5.8), а также сами
эти решения.
Такие значения
параметра
![]() называются собственными значениями, а
соответствующие им нетривиальные
решения – собственными функциями задачи
(5.7) – (5.8). Задачу нахождения таких
значений
называются собственными значениями, а
соответствующие им нетривиальные
решения – собственными функциями задачи
(5.7) – (5.8). Задачу нахождения таких
значений
![]() называют задачей Штурма – Лиувилля.
называют задачей Штурма – Лиувилля.
Найдем собственные значения и собственные функции задачи (5.7) – (5.8). Рассмотрим все возможные случаи:
1.
![]() ,
тогда общее решение уравнения (5.7) имеет
вид
,
тогда общее решение уравнения (5.7) имеет
вид
![]() .
.
Используя граничные условия (5.8), будем иметь
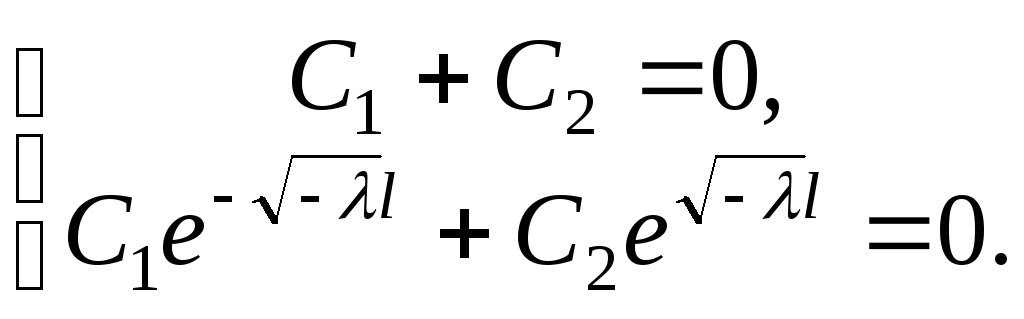
Так как определитель
![]() ,
то
,
то
![]() и, следовательно,
и, следовательно,
![]() ,
т.е. в этом случае нетривиальных решений
нет.
,
т.е. в этом случае нетривиальных решений
нет.
2.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Отсюда
.
Отсюда
![]() и
и
![]() .
.
3. При
![]() корни характеристического уравнения
корни характеристического уравнения
![]() и
и
![]() .
.
Используя граничные условия, получим
![]() ,
,
![]() ,
или
,
или
![]() .
.
Так как при
![]() мы опять получим
мы опять получим
![]() ,
то положим
,
то положим
![]() ,
,
![]() ,
,
![]() .
.
Отсюда получаем
![]() ,
,
![]() - собственные значения и соответствующие
им
- собственные значения и соответствующие
им
![]() - собственные функции.
- собственные функции.
Ни при каких других
значениях
![]() краевая задача (5.7) – (5.8) не имеет
нетривиальных решений. При
краевая задача (5.7) – (5.8) не имеет
нетривиальных решений. При
![]() уравнение
уравнение
![]()
имеет решение
![]() .
.
Используя
![]() и
и
![]() ,
получим решение
,
получим решение
![]() =
=![]()
![]() =
=![]()
![]()
задачи (5.4), удовлетворяющее граничным условиям.
Постоянные
![]() в этом выражении произвольные, а значения
k
нужно брать только положительные, так
как при отрицательных значениях
получаются решения того же вида.
в этом выражении произвольные, а значения
k
нужно брать только положительные, так
как при отрицательных значениях
получаются решения того же вида.
В силу линейности и однородности уравнения в (5.4) любая конечная сумма решений будет также решением. Это справедливо и для бесконечной суммы
![]() =
=![]() =
=![]()
![]() (5.9)
(5.9)
при любых значениях
коэффициентов
![]() ,
если этот ряд равномерно сходится и его
можно почленно дифференцировать дважды
по х
и по t.
Так как члены ряда (5.9) удовлетворяют
граничным условиям (5.2), то этим условиям
будет удовлетворять и сумма ряда, т.е.
функция
,
если этот ряд равномерно сходится и его
можно почленно дифференцировать дважды
по х
и по t.
Так как члены ряда (5.9) удовлетворяют
граничным условиям (5.2), то этим условиям
будет удовлетворять и сумма ряда, т.е.
функция
![]() =
=![]() .
Эти коэффициенты надо подобрать так,
чтобы эта сумма удовлетворяла также
начальным условиям. Таким образом, для
определения
.
Эти коэффициенты надо подобрать так,
чтобы эта сумма удовлетворяла также
начальным условиям. Таким образом, для
определения
![]() получаем
получаем
![]() ,
,
![]() , (5.10)
, (5.10)
которые представляют
собой разложения функций
![]() и
и
![]() в ряды Фурье по синусам в интервале
в ряды Фурье по синусам в интервале
![]() .
Умножая обе части первого из равенств
(5.10) на
.
Умножая обе части первого из равенств
(5.10) на
![]() и интегрируя на интервале
и интегрируя на интервале
![]() ,
учитывая, что
,
учитывая, что

получим
![]() .
.
Аналогично из второго равенства находим
![]() .
.
Таким образом, задача (5.4) решена.
Теорема 1. (о единственности решения смешанной краевой задачи для струны). Если уравнение (5.1) имеет решение, удовлетворяющее начальным условиям (5.3) и граничным условиям (5.2), то оно единственно.
Обоснование метода Фурье в случае неоднородного уравнения.
Решение задачи (5.5) будем искать в виде
![]() =
=![]() =
=![]()
![]() . (5.11)
. (5.11)
Очевидно, что оно
удовлетворяет однородным граничным
условиям задачи (5.5). Используя разложение
функции
![]() в интервале (0, l)
в ряд Фурье по синусам (собственным
функциям)
в интервале (0, l)
в ряд Фурье по синусам (собственным
функциям)
![]() ,
,
где
![]() ,
,
и подставляя (5.11) в уравнение задачи (5.5), получим равенство
![]() ,
,
из которого следует
![]() . (5.12)
. (5.12)
Используя однородные начальные условия из (5.5), получим
![]() =
=![]()
![]() ,
,
следовательно,
![]() ,
,
![]() =
=![]()
![]() =0,
=0,
следовательно
![]() .
.
Таким образом, мы получили задачу Коши:
![]() , (5.13)
, (5.13)
![]() .
.
Общим решением соответствующего однородного уравнения является
![]() . (5.14)
. (5.14)
Для нахождения
частного решения неоднородного уравнения
построим функцию Коши
![]() так, что
так, что
1.
![]() как функция от t
при любом фиксированном s
является решением однородного уравнения;
как функция от t
при любом фиксированном s
является решением однородного уравнения;
2.
![]() ,
,
![]() .
.
Для построения
функции Коши
![]() подчиним условиям
подчиним условиям
![]() ,
,
![]() ,
,
что в результате дает решение
![]() .
.
Заменив далее t на t – s, получим функцию Коши
![]() ,
,
которая при любом фиксированном значении s является решением однородного уравнения из (5.13). Теперь частное решение неоднородного уравнения получим по формуле
![]() .
.
Таким образом, общее решение уравнения из задачи (5.13)
![]() .
.
Используя начальные условия, получим
![]() ,
,
![]() ,
,
следовательно,
![]() .
.
Таким образом,
![]() и
и
![]() ,
,
![]() =
=![]() =
=![]()
![]() .
.
Сумма решений
![]() ,
,
![]() задач (5.4) и (5.5) дает решение смешанной
краевой задачи для неоднородного
уравнения с неоднородными начальными
и однородными граничными условиями.
задач (5.4) и (5.5) дает решение смешанной
краевой задачи для неоднородного
уравнения с неоднородными начальными
и однородными граничными условиями.
Пример.
Однородная струна, закрепленная на
концах
![]() ,
,
![]() ,
имеет в начальный момент времени форму
параболы, симметричной относительно
перпендикуляра, проведенного через
точку
,
имеет в начальный момент времени форму
параболы, симметричной относительно
перпендикуляра, проведенного через
точку
![]() .
Определить смещение точек струны от
прямолинейного положения равновесия,
предполагая, что начальные скорости
отсутствуют.
.
Определить смещение точек струны от
прямолинейного положения равновесия,
предполагая, что начальные скорости
отсутствуют.
Решение. Необходимо решить следующую задачу о свободных колебаниях струны:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Решение будем искать в виде (5.9)
![]()
![]() ,
,
где
![]() .
.
![]() .
.
Так образом, решением исходной задачи является функция
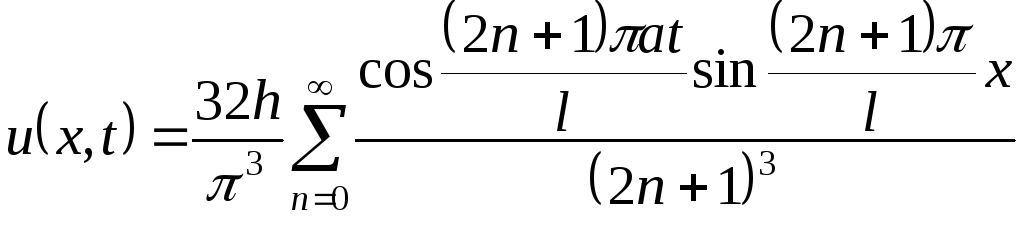 .
.
Колебания защепленной струны.
П усть
струна закреплена на концах. Оттянем
ее вверх, защепив в точке
усть
струна закреплена на концах. Оттянем
ее вверх, защепив в точке
![]() ,
и затем отпустим, предоставив ей совершать
свободные колебания. В этом случае
начальные условия будут иметь вид
,
и затем отпустим, предоставив ей совершать
свободные колебания. В этом случае
начальные условия будут иметь вид
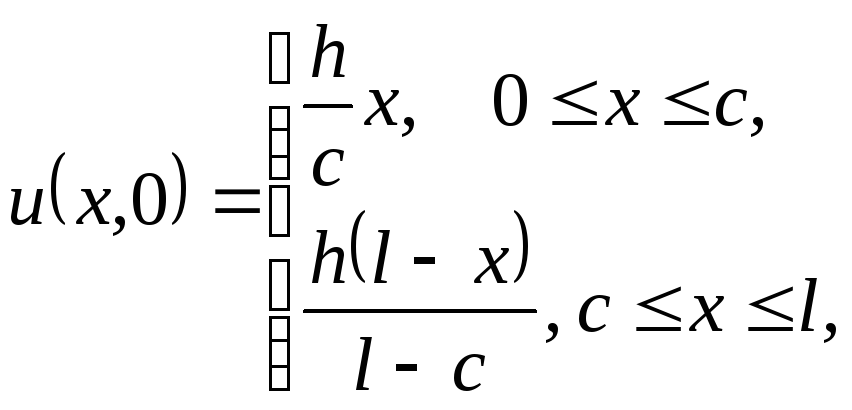 ,
,
![]() .
.
Применяя формулы (5.9) и
![]() ,
,
![]() ,
,
получим
![]() ,
,
![]() .
.
Следовательно, отклонение защепленной струны выражается равенством
![]() .
.
