Госы 5к Надя / ЛекцииТФДП / Мера Лебега

§23. Измеримые множества. Мера Лебега.

Определение 1. Множество Е задано на . Множество Е называется измеримым по Лебегу, если . Это общее значение называется мерой множества Е и обозначается m(E).

Свойство 1. Если Е - измеримо, то - измеримо.

Доказательство:

Е – измеримо, следовательно (по определению) . Докажем, что измеримо, то есть что

.

Действительно,

=1-=1-,

1-= 1-.

Следовательно, - измеримо.

Лемма 1. Пусть . Множество Е измеримо тогда и только тогда, когда =. (1)

Доказательство:

1. Необходимость.

Пусть Е измеримо. Докажем (1).

Так как Е измеримо, то по определению . Тогда по обобщению определения внутренней меры на промежуток

()- ,

=.

2. Достаточность.

Пусть верно (1). Докажем, что Е измеримо. Из (1) следует, что

()- .

По определению

()- .

Тогда . По определению множество Е измеримо.

§24. Основные теоремы об измеримых множествах.

Теорема 1. Пусть измеримые множества. Тогда:

а) множество измеримо и ;

б) если , , то .

Теорема 2. а) Пусть F, E - измеримые множества, . Тогда - измеримое множество.

б) - последовательность измеримых множеств, . Тогда множество измеримо.

Доказательство теоремы 1(б):

Пусть , , . Докажем, что Е измеримо, то есть что .

Так как , , то по свойству 3 внутренней меры . Так как множества измеримы , то

. (1)

Кроме того,

. (2)

По свойству 3 внешней меры

. (3)

Из (1)-(3) следует, что .

Доказательство теоремы 2(а):

1. Пусть - измеримое множество, произвольное измеримое множество.

а) Обозначим . Докажем, что измеримо.

Рассмотрим множество , . Пусть открытое множество.

Обозначим , , (1)

б) Докажем, что .

По определению внешней меры множество О можно выбрать так, чтобы

(*).

Кроме того,

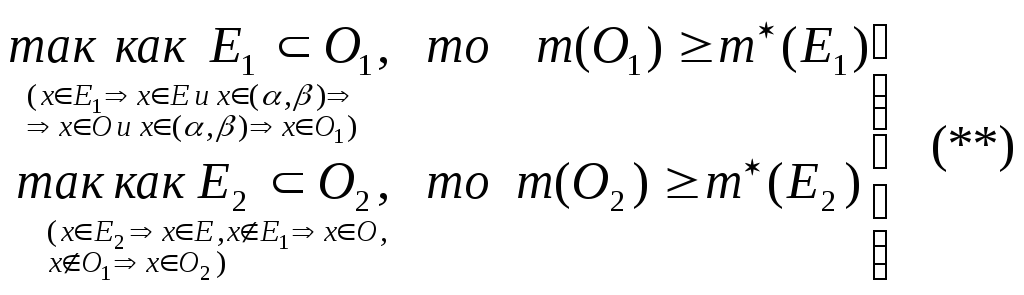
Складываем неравенства (**):

.

Вычитаем из всех трёх частей:

.

Переходим к пределу при .

в) где .

Можно доказать (аналогично предыдущему пункту), что . (2)

г) Е - измеримо

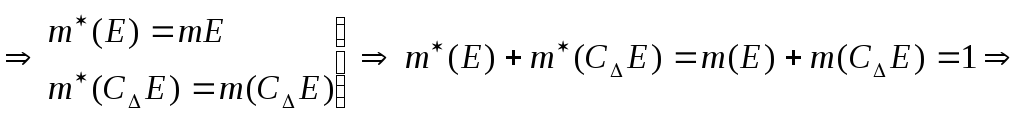
. (3)

д) .

Действительно,

1)

;

2) .

Итак, . По свойству 3 внешней меры , то есть

. (4)

е)

Действительно, пусть две возможности:

или

Тогда по свойству 3 внешней меры

,

.

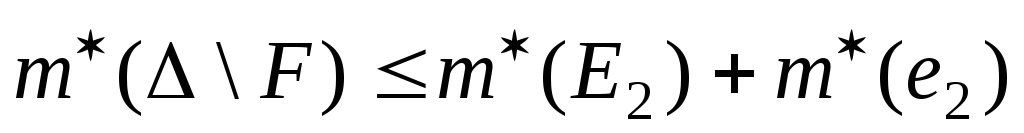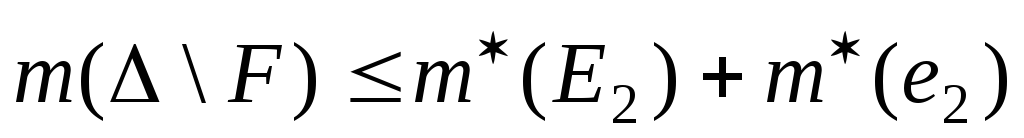. (5)

Из (3), (4) и (5) или

2. Пусть далее F-открытое множество

, .

.

E – измеримо множества измеримы. Тогда множество , , измеримо по теореме 1 б).

Итак, измеримо и .

3. Пусть, наконец, F- произвольное измеримое множество

F - измеримо

(по определению inf)

Так как

, то . (6)

Кроме того,

Действительно, пусть

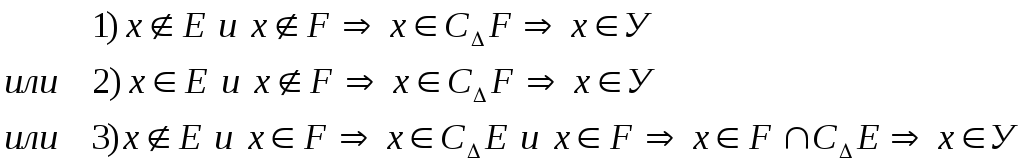
Включение доказано, отсюда следует, что

, так как . Тогда

F измеримо .

Переходим к пределу при то есть

. (7)

Кроме того,

. (8)

Тогда из (7), (8) следует, что измеримо.

Следствие из теоремы 2а). Пусть - измеримые множества, . Тогда Е измеримо и .

Доказательство:

1. Докажем, что Е измеримо. Пусть _,

Докажем, что .

(1)

(2)

(1)(2)

измеримо по условию, измеримо по свойству 1, отсюда следует, что Е измеримо по теореме 2 а).

2. 

Доказательство теоремы 1а):

Докажем, что Е измеримо.

измеримы.

1 шаг

Пусть

Докажем, что:

а);

б) , (для определённости можно считать, что m>k).

б) По построению

Пусть .

Пусть .

а) Обозначим . Докажем, что Е=А.

Пусть

или

Итак, .

Докажем, что .

Пусть ,

Возможны 2 случая:

1)

2)

Но .

Итак, . Таким образом, А=Е.

2 шаг

Докажем, что измеримы . По условию измеримы , .

измеримо измеримо и измеримо по условию измеримо и .

Далее по индукции: измеримо измеримо и измеримы по условию измеримо по теореме 2 а). По индукции измеримы и не пересекаются. Тогда по теореме 1 б) множество Е измеримо и Далее:

то есть .

Доказательство теоремы 2б):

Пусть , _.

Докажем, что .

а) Пусть

б) Пусть

измеримы измеримы измеримо Е измеримо.

Следствие. Если множество замкнуто, то оно измеримо.

Доказательство:

Пусть F - любое ограниченное замкнутое множество, . Обозначим .

F замкнуто .

Рассмотрим - открытое множество, так как

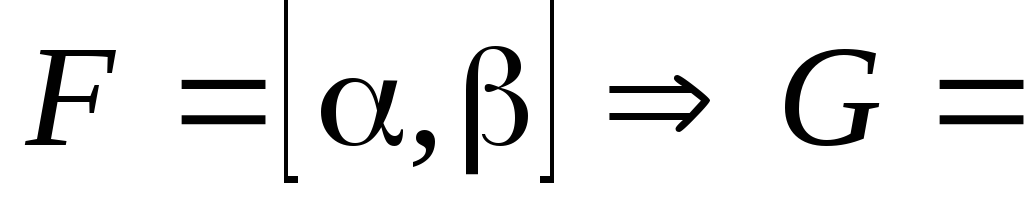
1. если  - открытое множество;

2. F - любое множество, не совпадающее с :

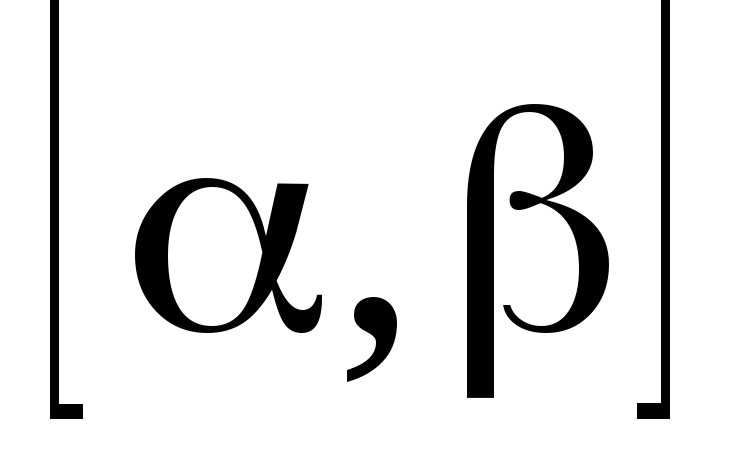не может быть предельной точкой множества F (так как F - замкнутое множество) , в которой нет точек из F любая точка из G - внутренняя, отсюда следует, что G открыто, следовательно, G измеримо. Но F измеримо по свойству 1.

5