
Госы 5к Надя / ЛекцииТФДП / измеримые функции
.doc§26. Измеримые функции
Пусть Е - измеримое множество, ЕR и задана функция f, область определения которой содержит Е.
Определение.
Функция
![]() называется измеримой
на
называется измеримой
на
![]() ,
если
,
если
![]() множество
множество
![]() измеримо.
измеримо.
Теорема 1. Пусть Е измеримо, f задана на Е. Функция f измерима тогда и только тогда, когда АR одно из множеств 1-3 измеримо:
1. Е(f ≤ A);
2. E(f ≥ A);
3. E(f < A).
Доказательство:
1. f измерима E(f ≤ A) измеримо.
) f измерима по определению E(f > A) измеримо АR. E(f ≤A)=E\E(f>A). По следствию из теоремы 2(а) множество E(f ≤ A) измеримо как дополнение измеримого множества до Е.
)Пусть E(f ≤ A) измеримо E(f > A) = E\E(f ≤ A) измеримо, следовательно, по определению f измерима.
2. f измерима E(f ≥ A) измеримо.
) f измерима. Докажем, что E(f≥A) измеримо.
Покажем методом встречных включений,
что
![]() .
.
а) xo
E(f≥A)
f(xo)≥A
![]()
![]() nN
nN
![]() nN
nN
![]() .
.
b)
![]()
![]() n
N
n
N
![]()
![]() n
N.
Переходя к пределу при n,
получим, что f(xo)≥A
xo
E(f
≥ A).
n
N.
Переходя к пределу при n,
получим, что f(xo)≥A
xo
E(f
≥ A).
Так как f
измерима, то
![]() измеримо n
N.
Следовательно, по теореме 2(б)
измеримо n
N.
Следовательно, по теореме 2(б)
![]() измеримо.
измеримо.
) E(f≥A) измеримо. Докажем, что f измерима.
Рассмотрим
множество E(f
> A).
Покажем,
что
 .
.
a)
Пусть xoE(f>A)
f(xo)
>A. Очевидно, что
noN:
![]()
![]()
xo
xo![]() .
.
b)
xo![]()
![]() ,
no
N
f(xo)>A
xoE(f>A).
,
no
N
f(xo)>A
xoE(f>A).
По условию
![]() измеримо nN
и по теореме 1(а) множество E(f>A)
измеримо
f по определению
измерима.
измеримо nN
и по теореме 1(а) множество E(f>A)
измеримо
f по определению
измерима.
3. Провести доказательство самостоятельно.
§27. Арифметические действия над измеримыми функциями
Теорема 2. Пусть f и g - измеримые функции. Тогда множество E(f >g) = {xE: f(x)>g(x)} измеримо.
Доказательство:
Занумеруем
рациональные числа
![]() .
Покажем методом встречных включений,
что
.
Покажем методом встречных включений,
что
![]() .
.
а) Пусть xoE(f>g) f(xo) > g(xo).
![]()
Q : f(xo)>
Q : f(xo)>![]() >g(xo)
f(xo)>
>g(xo)
f(xo)>![]() и
g(xo)<
и
g(xo)<![]()
xoE(f
>
xoE(f
>![]() )
и xoE(g
<
)
и xoE(g
<![]() )
xoE(f>
)
xoE(f>![]() )E(g<
)E(g<![]() )
xo
)
xo![]() .
.
б) Пусть xo![]()
noN
: xoE(f
>
noN
: xoE(f
>![]() )
и xoE(g
<
)
и xoE(g
<![]() )
f(xo)>
)
f(xo)>![]() и
g(xo)<
и
g(xo)<![]()
f(xo)>g(xo)
xoE(f>g).
f(xo)>g(xo)
xoE(f>g).
Так как f измерима, то
E(f
>![]() )
измеримо nN.
Так как g измерима,
то E(g
<
)
измеримо nN.
Так как g измерима,
то E(g
<![]() )
измеримо nN.
Следовательно, по теореме 2 множество
E(f
>
)
измеримо nN.
Следовательно, по теореме 2 множество
E(f
>![]() )E(g
<
)E(g
<![]() )
измеримо nN,
следовательно, по теореме1(а) множество
E(f
>g) измеримо.
)
измеримо nN,
следовательно, по теореме1(а) множество
E(f
>g) измеримо.
Теорема 3. Пусть функции f и g определены на измеримом множестве Е.
1) Если f измерима, k,rR, то функции kf и f +r измеримы на Е.
2) Если f и g измеримы на Е, то f ± g измерима на Е и fg измерима на Е.
3) Если f(х)≠0 хЕ, то 1/f ,g/f – измеримые функции на Е.
Доказательство:
1. а) Докажем, что функция kf измерима на Е, то есть что множество Е(kf >A) измеримо АR.
Рассмотрим неравенство kf >A.
Пусть k=0. Имеем 0>A
E(0>A)={xE:
0>A} - измеримо, так как Е и
- измеримые множества. Следовательно,
функция kf
измерима при k=0.
- измеримо, так как Е и
- измеримые множества. Следовательно,
функция kf
измерима при k=0.
Пусть k≠0, тогда
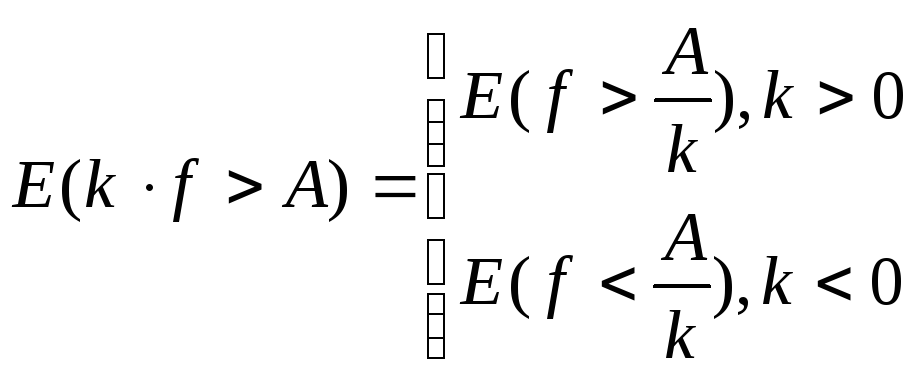 -
измеримо, так как f
измерима
kf
измерима.
-
измеримо, так как f
измерима
kf
измерима.
б) Докажем, что f+r измерима на Е.
f+r
– измерима на Е
множество E(f+r>A)
измеримо, но E(f+r>A)=E(f>A-r)
измеримо (так как f
измерима,
![]() ).
).
2. а) Докажем, что f±g измерима на Е.
f±g – измеримая функция множество Е(f ±g >A) AR измеримо.
Е(f±g>A)=Е(f
>A![]() g),
но функция (–g) измерима по пункту
1) данной теоремы, функция А
g),
но функция (–g) измерима по пункту
1) данной теоремы, функция А![]() g
измерима по тем же соображениям
по теореме 2 множество Е(f>A
g
измерима по тем же соображениям
по теореме 2 множество Е(f>A![]() g)
измеримо
f±g
измерима.
g)
измеримо
f±g
измерима.
б) Докажем, что fg измерима на Е.
Пусть
![]() .
Докажем, что f 2
измерима на Е, то есть множество Е(f
2>A) измеримо
АR.
.
Докажем, что f 2
измерима на Е, то есть множество Е(f
2>A) измеримо
АR.
E(f2>A)
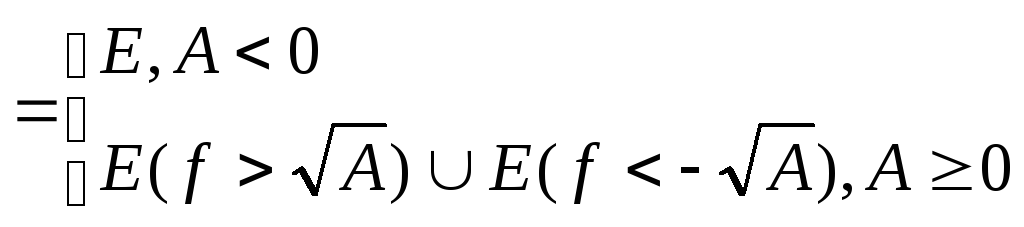 .
.
Очевидно, что
![]() и Е - измеримые множества, то есть
множество Е(f 2>A)
измеримо АR.
и Е - измеримые множества, то есть
множество Е(f 2>A)
измеримо АR.
Пусть далее
![]() .
Заметим fg=
.
Заметим fg=![]() .
Так как f±g
– измеримые функции, то функции (f±g)2
также измеримы
.
Так как f±g
– измеримые функции, то функции (f±g)2
также измеримы
![]() - измеримая функция, то есть fg
– измеримая функция.
- измеримая функция, то есть fg
– измеримая функция.
3. а) Докажем, что
![]() - измеримая функция на Е, то есть
множество
- измеримая функция на Е, то есть
множество
![]() измеримо АR.
измеримо АR.
![]() .
.
Пусть А=0, тогда
![]() .
.
П усть
А≠0, тогда
усть
А≠0, тогда
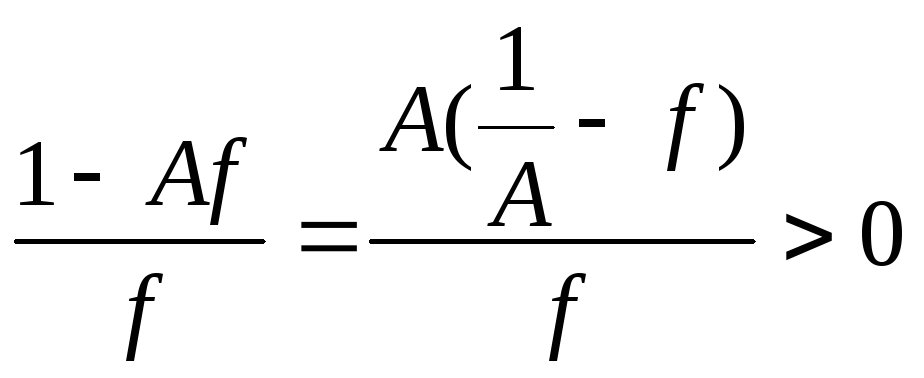 .
.
Е
 сли
А>0, то 0<f(x)<
сли
А>0, то 0<f(x)<![]() .
.
Если А<0, то f(x)<![]() или f(x)>0.
или f(x)>0.
Таким образом,
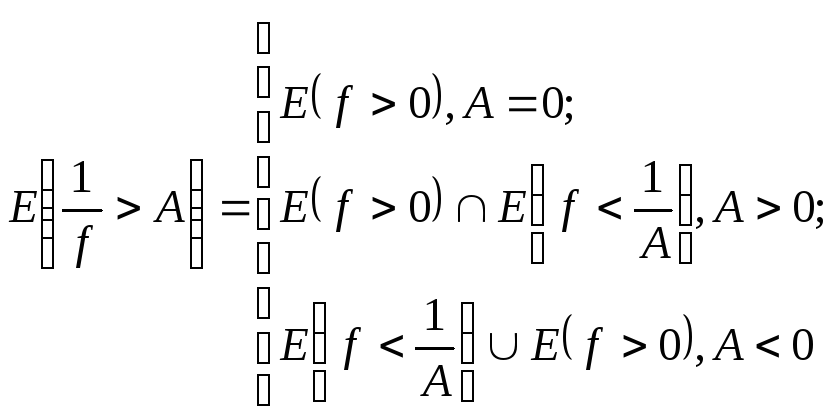 - измеримо АR.
- измеримо АR.
б) Докажем, что
![]() - измеримая функция на Е.
- измеримая функция на Е.
![]() измерима на Е, так как функции
измерима на Е, так как функции![]() и
и
![]() измеримы.
измеримы.
§28. Интеграл Лебега
Пусть Е – измеримое множество,
![]() -
измеримая функция на Е. Будем
предполагать, что
-
измеримая функция на Е. Будем
предполагать, что
![]() ограничена на Е, то есть существуют
ограничена на Е, то есть существуют
![]() ,
,
![]() такие, что
такие, что
![]() .
Разобьем
.
Разобьем
![]() на части точками
на части точками
![]() ,
,
![]() ,…,
,…,![]() .
Разбиение обозначим
.
Разбиение обозначим
![]() :
:
![]() .
Каждому полученному промежутку
.
Каждому полученному промежутку
![]() будет соответствовать множество
будет соответствовать множество
![]() =
=![]() ,
,
![]() .
.
Составим суммы:
![]() ,
,
![]() ,
которые назовём нижняя
и верхняя суммы Лебега.
,
которые назовём нижняя
и верхняя суммы Лебега.
Свойства множеств
![]() .
.
1.
![]() ,
,
![]() ;
;
2.
![]() - измеримо (так как
- измеримо (так как
![]() - измерима);
- измерима);
3.
![]() ;
;
4.
![]() (из
1-3).
(из
1-3).
Очевидно, что
![]() (из определения).
(из определения).
Упражнение. Доказать самостоятельно свойства 1-4.
Определение.
Функция суммируема
или интегрируема по Лебегу,
если при любом разбиении
![]() этого отрезка
этого отрезка![]() ,
где
,
где
![]() .
Общее значение этих пределов называется
интегралом Лебега
от функции
.
Общее значение этих пределов называется
интегралом Лебега
от функции
![]() на множестве Е и обозначается
на множестве Е и обозначается
![]() .
.
Таким образом,
![]() .
.
Свойства сумм Лебега
Теорема 1.
Пусть
![]() - некоторое разбиение отрезка
- некоторое разбиение отрезка
![]() ,
то есть
,
то есть
![]() .
Разбиение
.
Разбиение
![]() получается из Т добавлением новых
точек, то есть
получается из Т добавлением новых
точек, то есть
![]() ;
;
![]() ,
,
![]() - суммы Лебега, соответствующие разбиению
Т;
- суммы Лебега, соответствующие разбиению
Т;
![]() ,
,
![]() - суммы Лебега, соответствующие разбиению
- суммы Лебега, соответствующие разбиению
![]() .
Тогда
.
Тогда
![]() ,
,
![]() .
.
Доказательство:
Д оказательство
достаточно провести для случая добавления
одной точки, то есть
оказательство
достаточно провести для случая добавления
одной точки, то есть
![]() ,
,
![]() .
.
![]() ,
где
,
где
![]() .
.
Множество
![]() разбиваем на два множества:
разбиваем на два множества:
![]() ;
;
![]() .
Тогда
.
Тогда
![]() ;
;
![]() .
Следовательно,
.
Следовательно,
![]() ;
;
![]() .
.
Далее
![]() ,
,
![]() .
.
Так как
![]()
![]() ,
то
,
то
![]() .
Аналогично доказывается, что
.
Аналогично доказывается, что
![]() .
.
Теорема 2.
Для произвольных разбиений Т и
![]()
![]() ,
,
![]() (любая нижняя сумма Лебега не превосходит
любой верхней).
(любая нижняя сумма Лебега не превосходит
любой верхней).
Доказательство:
Рассмотрим разбиение
![]() .
Так как
.
Так как
![]() можно
получить из Т добавлением новых
точек из
можно
получить из Т добавлением новых
точек из
![]() ,
то по теореме 1
,
то по теореме 1
![]() ,
,
![]() (1).
(1).
С другой стороны,
![]() ,
то есть его можно получить из
,
то есть его можно получить из
![]() добавлением новых точек из Т. Тогда
по теореме 1,
добавлением новых точек из Т. Тогда
по теореме 1,
![]() ,
,
![]() (2). Кроме того,
(2). Кроме того,
![]() (3).
(3).
Из (1), (2), (3) следует, что
![]() ,
,
![]() .
.
Теорема 3. Пусть Е – измеряемое множество и
1)
![]() ограничена на множестве Е;
ограничена на множестве Е;
2)
![]() измерима на Е.
измерима на Е.
Тогда существует
![]() .
.
Доказательство:
Множество
![]() ограничено сверху, так как
ограничено сверху, так как
![]() ,
следовательно, существует
,
следовательно, существует
![]() .
Множество
.
Множество
![]() ограничено снизу, следовательно,
существует
ограничено снизу, следовательно,
существует
![]() .
Докажем, что
.
Докажем, что
![]() .
.
![]() ,
так как s,
S:
,
так как s,
S:
![]() .
Пусть
.
Пусть
![]() - некоторое разбиение
- некоторое разбиение
![]() ,
,
![]() и
и
![]() - нижняя и верхняя суммы Лебега,
соответствующие данному разбиению.
Тогда
- нижняя и верхняя суммы Лебега,
соответствующие данному разбиению.
Тогда
![]() ,
,
![]() ,
,
![]() .
.
Рассмотрим разность
![]() :
:
![]()
![]() .
.
При
![]()
![]() ,
следовательно,
,
следовательно,
![]() ,
то есть
,
то есть
![]() и функция
и функция
![]() интегрируема на Е.
интегрируема на Е.
§29. Свойства интеграла Лебега
Свойство 1 (теорема
о среднем). Пусть Е – измеримое
множество,
![]() – измеримая функция на Е и
– измеримая функция на Е и
![]() xE.
Тогда
xE.
Тогда
![]() .
.
Доказательство:
Фиксируем
![]() N.
Положим
N.
Положим
![]() ,
,
![]() .
Тогда
.
Тогда
![]() .
Разобьем отрезок [A;B]
точками
.
Разобьем отрезок [A;B]
точками
![]() и составим множества
и составим множества
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
.
Просуммируем эти неравенства по k:
![]() .
.
По свойству 4 множеств
![]() имеем:
имеем:
![]() .
.
Перейдем к пределу при
![]() :
:
![]() .
.
Так как n – любое
натуральное число, то, переходя к пределу
при
![]() ,
получим:
,
получим:
![]() .
.
Следствие 1.
Пусть
![]() ,
Е - измеримое множество. Тогда
,
Е - измеримое множество. Тогда
![]() .
.
Доказательство:
Возьмем
![]() и
и
![]() ,
тогда
,
тогда
![]()
![]() .
.
Следствие 2.
Если
![]()
![]() ,
,
![]() – измеримая функция на Е , Е –
измеримое множество, то
– измеримая функция на Е , Е –
измеримое множество, то
![]() .
.
Доказательство:
Так как
![]() ,
то возьмем а=0 (b=0),
получим
,
то возьмем а=0 (b=0),
получим
![]() .
.
Следствие 3.
Если
![]() ,
то для любой ограниченной функции
,
то для любой ограниченной функции
![]() ,
определенной на измеримом множестве
Е,
,
определенной на измеримом множестве
Е,
![]() .
.
Свойство 2.
Пусть
![]() ,
,
![]() при
при
![]() ,
,
![]() - измеримое множество. Пусть далее
- измеримое множество. Пусть далее
![]() – измеримая, ограниченная функция на
Е. Тогда
– измеримая, ограниченная функция на
Е. Тогда
![]()
![]() .
.
Доказательство:
Так как
![]() ограничена на Е, то
ограничена на Е, то
![]()
![]() .
.
I. Докажем свойство для
случая двух множеств:
![]() ,
,
![]() .
Возьмем любое разбиение Т отрезка
[A,B]:
T: A=
.
Возьмем любое разбиение Т отрезка
[A,B]:
T: A=![]() .
Составим множества
.
Составим множества
![]()
![]() ,
,
![]() ,
,
![]() .
.
Так как
![]() - множество тех точек из
- множество тех точек из
![]() ,
для которых
,
для которых
![]() ,
то
,
то
![]() .
Аналогично,
.
Аналогично,
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
Кроме того,
.
Кроме того,
![]()
![]() .
.
Таким образом,
![]() ,
,
![]() .
.
Умножим части равенства на
![]() ,
получим:
,
получим:
![]()
Просуммируем эти равенства по k:
![]() .
.
Перейдем в последнем равенстве к пределу
при
![]() :
:
![]() .
.
II. Случай
![]() ,
,
![]() при
при
![]() .
В этом случае справедливо утверждение:
.
В этом случае справедливо утверждение:
![]()
![]() .
.
Доказательство проводится методом математической индукции (Самостоятельно!).
III. Случай
![]() ,
,
![]() при
при
![]() .
.
По теореме 1(б) (основные теоремы об
измеримых множествах)
![]() ,
то есть ряд сходится
,
то есть ряд сходится
![]() ,
где
,
где
![]() ,
то есть
,
то есть
![]() при
при
![]() .
.
