
Госы 5к Надя / ЛекцииТФДП / измеримые функции
.doc
Рассмотрим множество Е=![]() ,
где
,
где
![]() .
Из I и II
следует, что
.
Из I и II
следует, что
![]() .
(1)
.
(1)
Так как
![]() ,
то по свойству 1
,
то по свойству 1
![]() (2)
(2)
Из (2) по теореме о пределе промежуточной
последовательности следует, что
![]() при
при
![]() .
Перейдем в (1) к пределу при
.
Перейдем в (1) к пределу при
![]() .
Получим:
.
Получим:
![]()
![]() .
.
Свойство 3.
Е – измеримое множество,
![]() ,
,
![]() – измеримые функции на Е. Тогда
– измеримые функции на Е. Тогда
![]() .
.
Доказательство:
Пусть
![]() ,
,
![]() .
Разобьем отрезки [a,b]
и [A,B]
точками
.
Разобьем отрезки [a,b]
и [A,B]
точками
![]() ,
,
![]()
и рассмотрим множества
![]() ,
,
![]() ,
,
![]()
![]() .
.
Обозначим
![]() =
=![]()
![]()
![]() .
Очевидно:
.
Очевидно:
1)
![]() .
.
Докажем это методом встречных включений.
а) xE
![]() ;
;
b)
![]()
![]()
xE.
xE.
2)
![]() попарно не пересекаются.
попарно не пересекаются.
Следовательно, по свойству 2
![]() .
.
На множестве
![]() имеем:
имеем:
![]() .
По свойству 1:
.
По свойству 1:
![]() .
.
Складывая все такие неравенства, получим:
![]() .
.
Найдем сумму:
![]() .
.
Но
![]() =
=![]() =
=![]()
![]() =
=![]() .
.
Следовательно,
![]() =
=![]() =
=![]() .
.
Аналогично,
![]()
![]() .
.
Следовательно,
![]() .
.
Пусть
![]() .
Переходя в последнем неравенстве к
пределу при
.
Переходя в последнем неравенстве к
пределу при
![]() ,
получим:
,
получим:
![]() .
.
Свойство 4.
Пусть Е – измеримое множество,
![]() измерима на Е, сR,
тогда
измерима на Е, сR,
тогда
![]() .
.
Доказательство:
1) Случай
![]() - очевидно.
- очевидно.
2) Случай
![]() .
.
Пусть
![]() .
Разобьем отрезок [A,B]
точками
.
Разобьем отрезок [A,B]
точками
![]() и рассмотрим множества
и рассмотрим множества
![]() ,
определяемые обычным способом. Тогда
,
определяемые обычным способом. Тогда
![]() .
.
На
![]() имеем:
имеем:
![]() .
По свойству 1:
.
По свойству 1:
![]() .
.
Суммируем все такие неравенства:
![]() ,
,
где s, S
– суммы Лебега для функции
![]() .
Переходя в последнем неравенстве к
пределу при
.
Переходя в последнем неравенстве к
пределу при
![]() ,
получим:
,
получим:
![]() .
.
3) Случай
![]() .
.
Заметим, что
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() =
=![]() и
и
![]() .
.
Теорема 5.
Пусть
![]() – измеримая и ограниченная функция на
измеримом множестве Е. Тогда
– измеримая и ограниченная функция на
измеримом множестве Е. Тогда
![]()
![]() .
.
Доказательство:
Введем в рассмотрение функции:
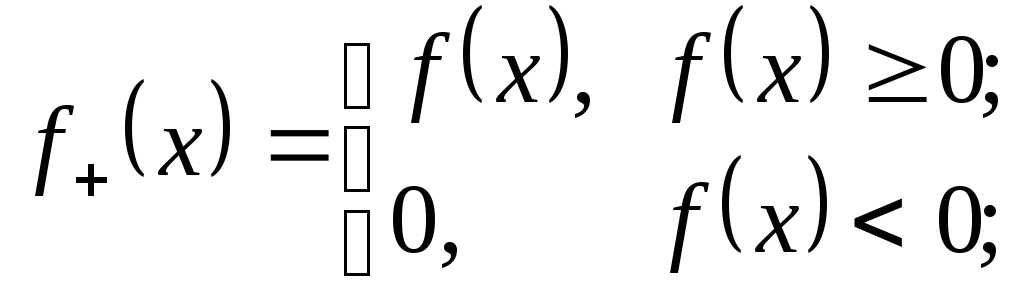 и
и
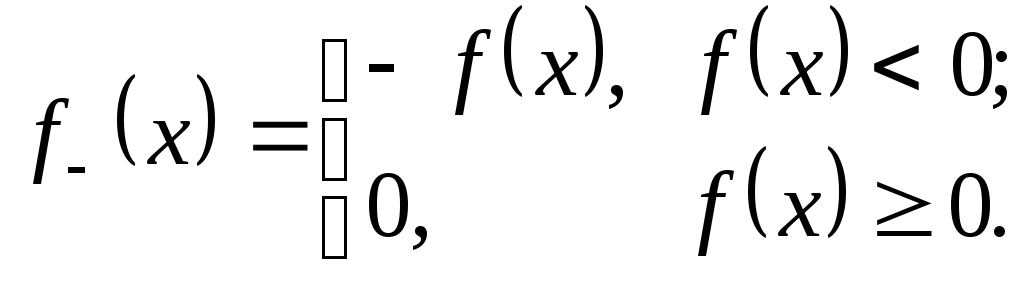
Функции
![]() и
и
![]() – измеримые, неотрицательные функции,
так как
– измеримые, неотрицательные функции,
так как
![]() – измерима, при этом
– измерима, при этом
![]() ,
,
![]()
![]() .
.
Тогда
![]() ,
,
![]() ,
,
![]() .
.
