
- •§1. Определение пространства .
- •§2. Ряд Фурье.
- •Ортонормированные системы в евклидовом пространстве.
- •2. Ортонормированные системы в k[] и k[a,b].
- •3. Определение ряда Фурье.
- •4. Замкнутые системы в евклидовых пространствах.
- •§3. Тригонометрический ряд Фурье.
- •1. Замкнутость тригонометрической системы.
- •2. Тригонометрическая система в пространстве интегрируемых функций.
- •3. Ряд Фурье по тригонометрической системе (3.2).
- •4.Тригонометрический ряд Фурье в пространстве .
- •5. Ряд Фурье чётных и нечётных функций. Разложение в ряд по синусам или косинусам.
- •Комплексная форма записи тригонометрического ряда Фурье.
- •§ 4. Поточечная и равномерная сходимость тригонометрического ряда Фурье
- •1. Свойства интегрируемых функций
- •2. Интегральное представление частичных сумм тригонометрического ряда Фурье
- •3. Необходимое и достаточное условие сходимости ряда Фурье в точке
- •4.Достаточные условия поточечной сходимости ряда Фурье.
- •5. Примеры.
§1. Определение пространства .
Приведем очень важный в дальнейшем пример евклидова пространства.
Определение 4.1.Функцияf(x)
называется кусочно-непрерывной на![]() ,
если она непрерывна во всех точках
интервала
,
если она непрерывна во всех точках
интервала![]() ,
за исключением, быть может конечного
числа точек
,
за исключением, быть может конечного
числа точек![]() таких, что
таких, что![]() и для любого
и для любого![]() существуют односторонние пределы
существуют односторонние пределы![]() .
.
Пример 1.1Обозначим через![]() пространство кусочно-непрерывных на
пространство кусочно-непрерывных на![]() функций, удовлетворяющих следующим
условиям:
функций, удовлетворяющих следующим
условиям:
Любая функция
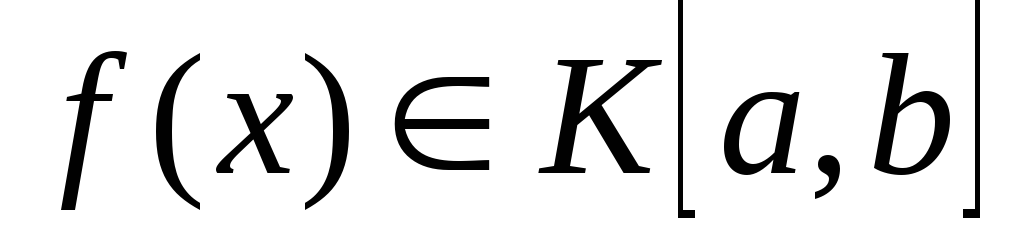 непрерывна на
непрерывна на ,
за исключением, быть может конечного
числа точек разрыва первого рода
,
за исключением, быть может конечного
числа точек разрыва первого рода ,
в которых
,
в которых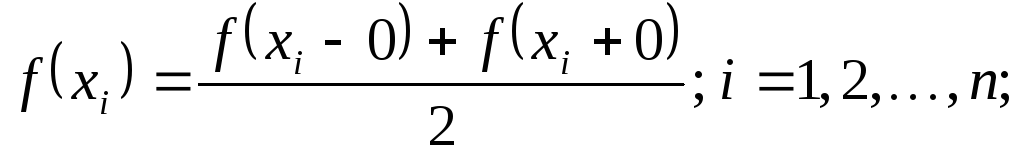 (3.1)
(3.1)Существуют
 и
и (4.1)
(4.1)
Множество
![]() является линейным пространством,
поскольку, если
является линейным пространством,
поскольку, если![]() ,
то
,
то![]() функция
функция![]() также удовлетворяет условиям 1), 2), то
есть
также удовлетворяет условиям 1), 2), то
есть![]() .
.
Определим на
![]() скалярное произведение по формуле:
скалярное произведение по формуле:
![]() .
(5.1)
.
(5.1)
Интеграл Римана в формуле (5.1) существует,
поскольку
![]() является ограниченной функцией с
конечным числом точек разрыва.
является ограниченной функцией с
конечным числом точек разрыва.
Справедливость аксиом скалярного
произведения 2), 3), 4) вытекает из линейных
свойств интеграла. Проверим выполнение
аксиомы 1). Неравенство
![]() очевидно. Предположим, что
очевидно. Предположим, что![]() .
(6.1)
.
(6.1)
Так как
![]() ,
то отрезок
,
то отрезок![]() распадается на конечное число промежутков
точками
распадается на конечное число промежутков
точками![]() так, что на любом интервале
так, что на любом интервале![]() ,
где
,
где![]() ,
функция
,
функция![]() непрерывна. При этом
непрерывна. При этом

Из равенства (6.1) вытекает, что
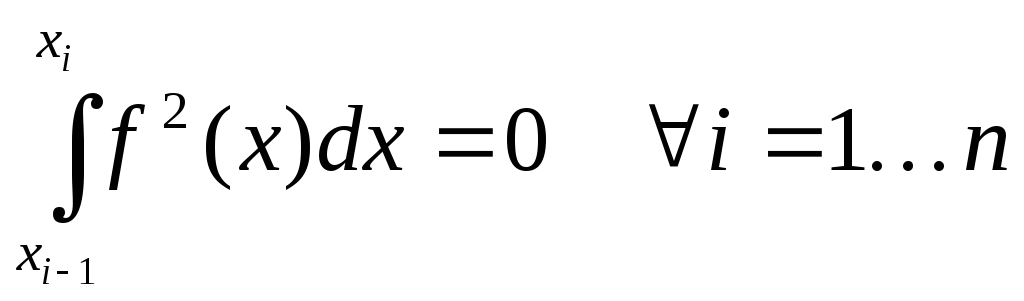 (7.1)
(7.1)
Определим на отрезке
![]() новую функцию
новую функцию
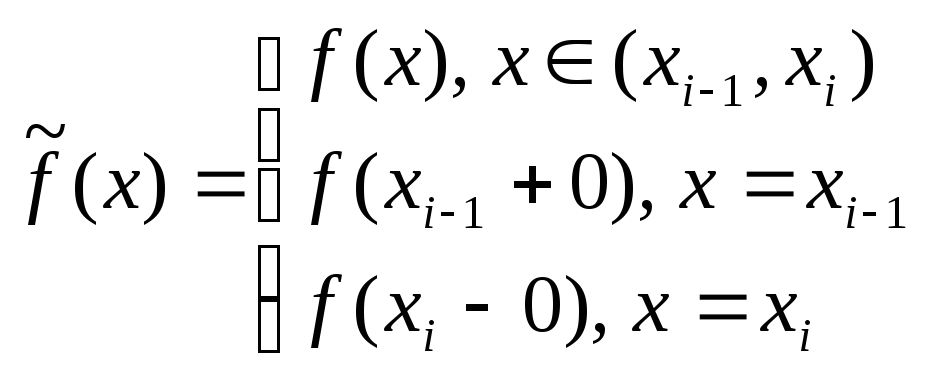
Легко видеть, что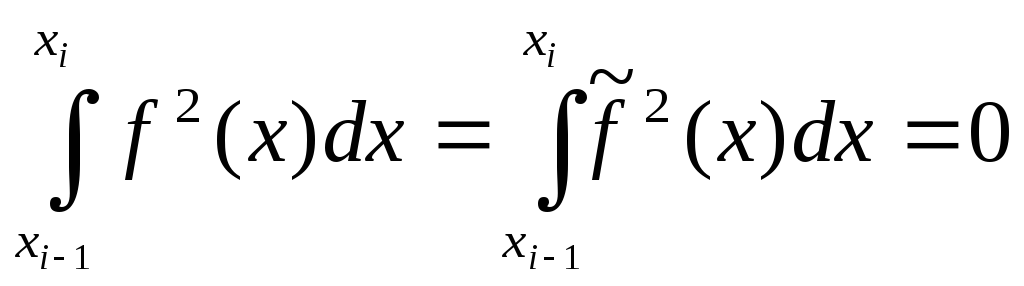 (8.1)
(8.1)
Это равенство вытекает из следующего свойства интеграла Римана
Теорема 2.1. Если функции![]() и
и![]() интегрируемы на отрезке
интегрируемы на отрезке![]() и совпадают везде на отрезке
и совпадают везде на отрезке![]() ,
за исключением конечного числа точек,
то
,
за исключением конечного числа точек,
то![]() .
.
Доказательство теоремы 2.1 вытекает из
того, что если функция
![]() равна 0 везде на отрезке
равна 0 везде на отрезке![]() ,
за исключением конечного числа точек,
то
,
за исключением конечного числа точек,
то![]() .
.
Задача 1.1.Доказать это утверждение.
Из равенства (8.1) и из непрерывности
функции
![]() следует, что
следует, что![]() на
на![]() .
Поэтому
.
Поэтому![]() на
на![]() .
Отсюда и (3.1), получим, что
.
Отсюда и (3.1), получим, что![]() на
на![]() .
.
Таким образом, пространство
![]() является евклидовым пространством.
является евклидовым пространством.
Определение5.1.Линейное
пространствоL
называется бесконечномерным, если![]() вL найдется
вL найдется![]() линейно независимых элементов.
линейно независимых элементов.
Утверждение3.1.Линейное
пространство
![]() –бесконечномерно.
–бесконечномерно.
Доказательство.
Возьмем любое
![]() .
Рассмотрим функции
.
Рассмотрим функции
![]() ,
(9.1)
,
(9.1)
где
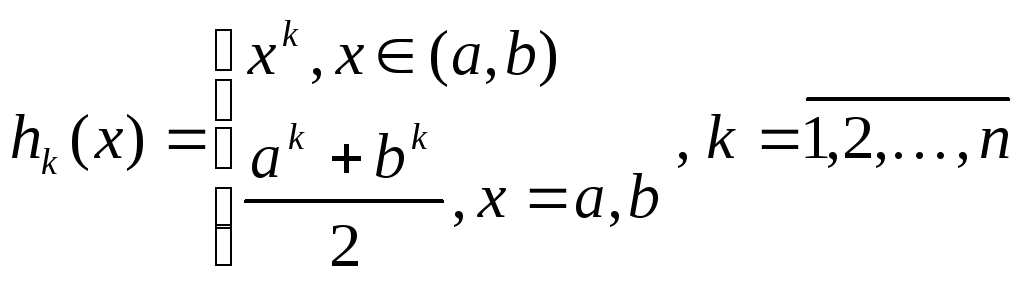 .
.
Если предположить, что функции (9.1)
линейно
![]() зависимы,
то
зависимы,
то![]() такие, что
такие, что![]() и
и![]() .
.
Это равенство означает, что многочлен
степени не больше
![]() имеет более
имеет более![]() корней. Противоречие. Следовательно,
система (9.1) линейно независима. Утверждение
доказано.
корней. Противоречие. Следовательно,
система (9.1) линейно независима. Утверждение
доказано.
Отметим, что согласно утверждениям 1.1,
1.2, пространство
![]() является нормированным и метрическим
с нормой
является нормированным и метрическим
с нормой и метрикой
и метрикой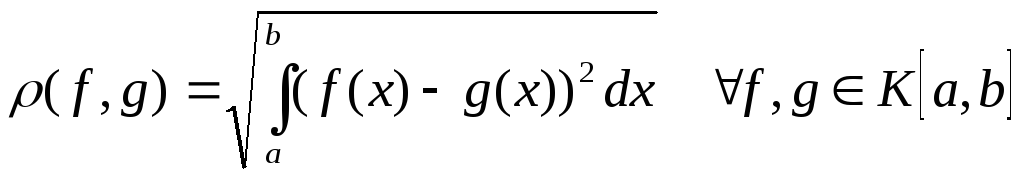 .
(10.1)
.
(10.1)
Определение 6.1.Будем говорить,
что последовательность функций![]() сходится в среднем к функции
сходится в среднем к функции![]() (это будем обозначать так:
(это будем обозначать так:![]() в среднем, или
в среднем, или![]() в среднем), если
в среднем), если![]() по метрике (10.1), то есть
по метрике (10.1), то есть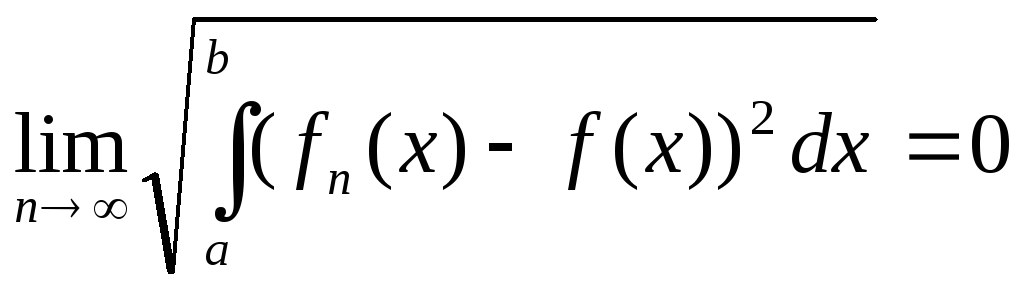 .
.
Помимо сходимости в среднем в пространстве
![]() будут рассмотрены еще два типа сходимости:
обычная поточечная и равномерная
сходимости.
будут рассмотрены еще два типа сходимости:
обычная поточечная и равномерная
сходимости.
Для удобства чтения напомним соответствующие определения.
Определение 7.1.Последовательность
функций![]() сходится к функции
сходится к функции![]() в точке
в точке![]() ,
если
,
если![]() .
(При фиксированном
.
(При фиксированном![]() этот предел представляет собой предел
числовой последовательности).
Последовательность функций
этот предел представляет собой предел
числовой последовательности).
Последовательность функций![]() сходится к функции
сходится к функции![]() на множествеХ поточечно, если
на множествеХ поточечно, если![]() сходится к
сходится к![]() в каждой точке множестваХ.
в каждой точке множестваХ.
Определение 8.1.Последовательность
функций![]() сходится к функции
сходится к функции![]() равномерно на множествеХ (это
обозначается так:
равномерно на множествеХ (это
обозначается так:![]() ),
если
),
если![]() и
и![]() .
.
Задача 2.1.Доказать, что если![]() и
и![]() ,
то
,
то![]() в среднем и поточечно на
в среднем и поточечно на
![]() .
.
Приведем примеры, показывающие, что из сходимости в среднем не следует поточечной и равномерной сходимости, и что из поточечной сходимости не следует сходимости в среднем, а, следовательно и равномерной.



Все рассмотренные выше определения
различных типов сходимостей функциональных
последовательностей естественным
образом переносятся на функциональные
ряды. Пусть
![]() естьn-я частичная сумма
функционального ряда
естьn-я частичная сумма
функционального ряда
![]() (11.1)
(11.1)
Определение 9.1.Говорят, что
ряд (11.1) сходится в среднем, либо в точке![]() ,
либо на множестве Х, если, соответственно,
последовательностьn-ых
частичных сумм
,
либо на множестве Х, если, соответственно,
последовательностьn-ых
частичных сумм![]() сходится в среднем к
сходится в среднем к![]() ,
либо в точке
,
либо в точке![]() к
к![]() ,
либо поточечно на Х, либо
,
либо поточечно на Х, либо![]() .
.
