
- •§1. Определение пространства .
- •§2. Ряд Фурье.
- •Ортонормированные системы в евклидовом пространстве.
- •2. Ортонормированные системы в k[] и k[a,b].
- •3. Определение ряда Фурье.
- •4. Замкнутые системы в евклидовых пространствах.
- •§3. Тригонометрический ряд Фурье.
- •1. Замкнутость тригонометрической системы.
- •2. Тригонометрическая система в пространстве интегрируемых функций.
- •3. Ряд Фурье по тригонометрической системе (3.2).
- •4.Тригонометрический ряд Фурье в пространстве .
- •5. Ряд Фурье чётных и нечётных функций. Разложение в ряд по синусам или косинусам.
- •Комплексная форма записи тригонометрического ряда Фурье.
- •§ 4. Поточечная и равномерная сходимость тригонометрического ряда Фурье
- •1. Свойства интегрируемых функций
- •2. Интегральное представление частичных сумм тригонометрического ряда Фурье
- •3. Необходимое и достаточное условие сходимости ряда Фурье в точке
- •4.Достаточные условия поточечной сходимости ряда Фурье.
- •5. Примеры.
§2. Ряд Фурье.
Ортонормированные системы в евклидовом пространстве.
Здесь и в дальнейшем будем считать, что Е есть бесконечномерное евклидово пространство.
Определение 1.2.Элементы![]() называются ортогональными, если
называются ортогональными, если![]() .
.
Определение 2.2.Последовательность элементов из Е
![]() (1.2)
(1.2)
называется ортогональной системой,
если
![]() .
.
Если дополнительно
![]() ,
то последовательность (1.2) называется
ортонормированной системой.
,
то последовательность (1.2) называется
ортонормированной системой.
Определение 3.2.Последовательность элементов линейного пространства
![]() (2.2)
(2.2)
называется линейно независимой, если
![]() элементы
элементы![]() линейно независимы.
линейно независимы.
Из определения 5.1 нетрудно вывести, что в любом бесконечномерном линейном пространстве существует линейно независимая последовательность элементов.
Если (2.2) линейно независимая последовательность из Е, то с помощью известного процесса ортогонализации Шмидта из нее получим бесконечную ортонормированную систему (1.2). Таким образом, в любом бесконечномерном евклидовом пространстве надеется бесконечная ортонормированная система.
Заметим также, что из курса линейной алгебры известно, что любая ортонормированная система линейно независима.
2. Ортонормированные системы в k[] и k[a,b].
В качестве основного примера
ортонормированной системы рассмотрим
в пространстве K[![]() ]
последовательность
]
последовательность
![]() (3.2)
(3.2)
которая называется тригонометрической системой.
Легко доказать следующее
Утверждение 1.2. Тригонометрическая система (3.2) ортонормированна.
Доказательство.
По определению ортонормированной системы, мы должны показать:
1)
![]()
2)
![]()
1) Напомним, что
![]()
(![]() )=
)=![]() .
.
Будем брать два произвольных элемента из тригонометрической системы (3.2) и показывать, что их скалярное произведение равно нулю.
![]()
![]()
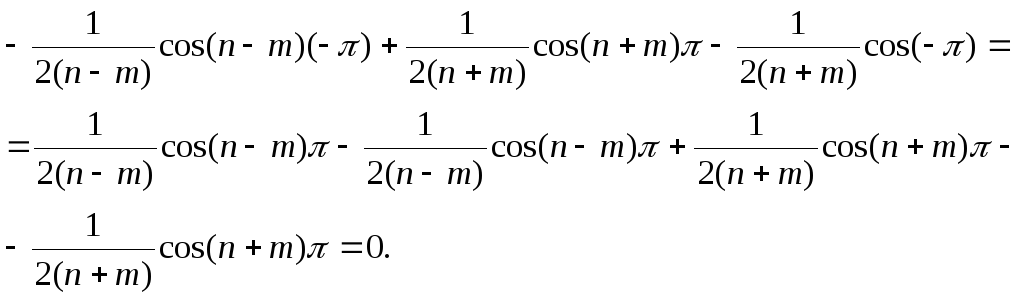
Аналогично проверяются равенства:
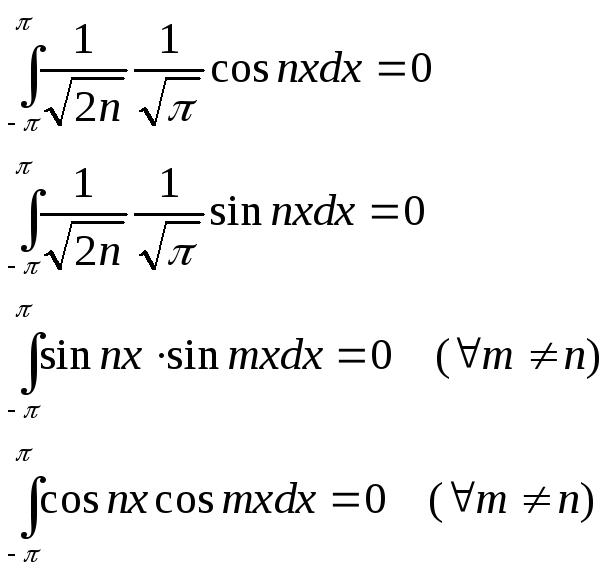 (*)
(*)
Таким образом, система (3.2) является ортогональной.
Докажем, что (3.2) является ортонормированной.
Напомним, что
![]()
![]()
Будем брать произвольный элемент из системы (3.2) и показывать, что его норма равна единице.
Произвольный элемент может иметь один из трех видов:
![]() или
или![]() .
.
Рассмотрим каждый из случаев:
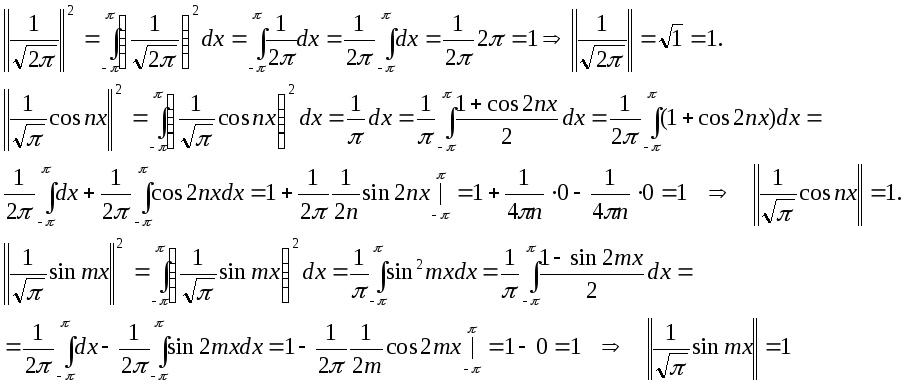
Таким образом, из 1)-2)
![]() система
(3.2) является ортонормированной. Теорема
доказана.
система
(3.2) является ортонормированной. Теорема
доказана.
Задача 1.2. Докажите равенства (*) утверждения 1.2.
Докажем вспомогательное утверждение.
Утверждение 2.2. Если функция![]() Т-периодична и интегрируема на любом
отрезке, то
Т-периодична и интегрируема на любом
отрезке, то
![]()
Доказательство.
![]() Сделаем в первом интеграле замену
переменной
Сделаем в первом интеграле замену
переменной![]() так
как
так
как![]() имеет
периодT. Следовательно,
имеет
периодT. Следовательно,
![]() Утверждение доказано.
Утверждение доказано.
Замечание 1.2. Из этого утверждения
вытекает, что для Т-периодической функции![]() интегралы
по любому отрезку с длиной, равной
периоду Т, совпадают и равны
интегралы
по любому отрезку с длиной, равной
периоду Т, совпадают и равны![]() .
Отсюда, в частности, следует, что
тригонометрическая система (3.2)
ортонормированна в пространствеK[a,b],
если
.
Отсюда, в частности, следует, что
тригонометрическая система (3.2)
ортонормированна в пространствеK[a,b],
если![]() .
.
Действительно, все функции системы
(3.2) 2![]() -периодичны,
-периодичны,![]() .
Поэтому
.
Поэтому![]()
![]()
Аналогично доказывается ортогональность других элементов системы (3.2).
Рассмотрим теперь пространство K[-![]() ]
с произвольным
]
с произвольным![]() >0.
Покажем, что тригонометрическая система
>0.
Покажем, что тригонометрическая система![]() (4.2)
(4.2)
ортонормированна в этом пространстве.
Найдем, например,
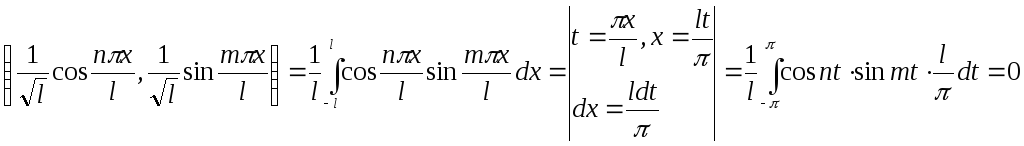 т.к.
система (3.2) ортонормированна.
т.к.
система (3.2) ортонормированна.
Аналогично доказывается ортогональность остальных функций из (4.2). С помощью замены переменной также доказывается, что все функции системы (4.2) нормированы.
Замечание 2.2. Поскольку все функции
из системы (4.2) имеют период 2![]() ,
то из утверждения 2.2 вытекает, что система
(4.2) ортонормированна в произвольном
пространствеK[a,b],
если
,
то из утверждения 2.2 вытекает, что система
(4.2) ортонормированна в произвольном
пространствеK[a,b],
если![]() .
.
