
- •§1. Определение пространства .
- •§2. Ряд Фурье.
- •Ортонормированные системы в евклидовом пространстве.
- •2. Ортонормированные системы в k[] и k[a,b].
- •3. Определение ряда Фурье.
- •4. Замкнутые системы в евклидовых пространствах.
- •§3. Тригонометрический ряд Фурье.
- •1. Замкнутость тригонометрической системы.
- •2. Тригонометрическая система в пространстве интегрируемых функций.
- •3. Ряд Фурье по тригонометрической системе (3.2).
- •4.Тригонометрический ряд Фурье в пространстве .
- •5. Ряд Фурье чётных и нечётных функций. Разложение в ряд по синусам или косинусам.
- •Комплексная форма записи тригонометрического ряда Фурье.
- •§ 4. Поточечная и равномерная сходимость тригонометрического ряда Фурье
- •1. Свойства интегрируемых функций
- •2. Интегральное представление частичных сумм тригонометрического ряда Фурье
- •3. Необходимое и достаточное условие сходимости ряда Фурье в точке
- •4.Достаточные условия поточечной сходимости ряда Фурье.
- •5. Примеры.
3. Определение ряда Фурье.
Если Lконечномерное
евклидово пространство с базисом![]() то любой элемент
то любой элемент![]() можно разложить по этому базису, то есть
можно разложить по этому базису, то есть![]() где
где![]() .
.
В случае бесконечномерного евклидова
пространства Е разложение элемента
![]() по бесконечной ортонормированной
системе называется рядом Фурье.
по бесконечной ортонормированной
системе называется рядом Фурье.
Пусть (1.2) является ортонормированной системой в евклидовом пространстве Е.
Определение 3.2. Рядом
Фурье элемента![]() по ортонормированной системе (1.2)
называется ряд
по ортонормированной системе (1.2)
называется ряд
![]() (5.2)
(5.2)
где
![]() Числа
Числа![]() называются коэффициентами Фурье или
координатами элемента
называются коэффициентами Фурье или
координатами элемента![]() в системе (1.2). Выражение
в системе (1.2). Выражение![]() называетсяn-й частичной
(или просто частичной) суммой ряда Фурье
(5.2).
называетсяn-й частичной
(или просто частичной) суммой ряда Фурье
(5.2).
Определение 4.2. Говорят,
что ряд Фурье (5.2) сходится в среднем
(или по норме Е), если![]() такая, что
такая, что
![]() (6.2)
(6.2)
Если выполнено равенство (6.2), то будем
говорить, что ряд (5.2) сходится в среднем
к элементу
![]() и писать
и писать![]()
Основной целью параграфа является
изучение вопроса о том, в каких случаях
ряд Фурье элемента
![]() сходится к
сходится к![]() в среднем.
в среднем.
Исследуем для начала вопрос о просто сходимости ряда Фурье.
Теорема 1.2. Если Е-гильбертово
пространство, то ряд Фурье (5.2) элемента![]() сходится для любой ортонормированной
системы (1.2).
сходится для любой ортонормированной
системы (1.2).
Для доказательства теоремы нам потребуется вспомогательное утверждение относительно свойств ортонормированных систем в евклидовых пространствах.
Лемма 1.2. Если Е-евклидово
пространство и (1.2) ортонормированная
система в Е, то![]() имеет место соотношение (равенство
Бесселя):
имеет место соотношение (равенство
Бесселя):
![]() (7.2)
(7.2)
а также равенство
![]() (8.2)
(8.2)
которое называется неравенством Бесселя.
Здесь
![]() - коэффициенты Фурье элемента
- коэффициенты Фурье элемента![]() .
.
Доказательство.

поскольку система {![]() }
– ортонормированна.
}
– ортонормированна.
Равенство Бесселя (7.2) доказано. Из него, в частности, следует, что
![]()
Следовательно, все частичные суммы
ряда в (8.2) ограничены. Поэтому этот ряд
сходится. Переходя в последнем неравенстве
к пределу при
![]() ,
получим неравенство (8.2) . Лемма доказана.
,
получим неравенство (8.2) . Лемма доказана.
Замечание 3.2. Из неравенства
Бесселя, в частности следует, что ряд
слева в (8.2) сходится и, значит, коэффициенты
Фурье![]() для любого элемента
для любого элемента![]() .
.
Доказательство теоремы 1.2.
Докажем, что последовательность
![]() фундаментальна в Е. Имеем при
фундаментальна в Е. Имеем при![]()
 где
где![]() остаток ряда
остаток ряда![]() Из неравенства Бесселя следует, что
этот ряд сходится и, значит,
Из неравенства Бесселя следует, что
этот ряд сходится и, значит,![]() Поэтому
Поэтому![]()
Следовательно,
![]() таких, что
таких, что![]() .
Таким образом, {
.
Таким образом, {![]() }
фундаментальная последовательность.
А так как Е полное пространство, то
}
фундаментальная последовательность.
А так как Е полное пространство, то![]()
![]() такая, что
такая, что![]() .
Теорема доказана.
.
Теорема доказана.
4. Замкнутые системы в евклидовых пространствах.
Рассмотрим еще одно важное свойство ряда Фурье.
Теорема 3.2. Если (1.2) есть
ортонормированная система в пространстве
Е, то![]() и
и![]() имеет место неравенство
имеет место неравенство
![]() (9.2)
(9.2)
где
![]() есть
есть![]() -я
частичная сумма ряда Фурье функции
-я
частичная сумма ряда Фурье функции![]() .
.
Доказательство.
Так как система
![]() ортонормированна, то
ортонормированна, то
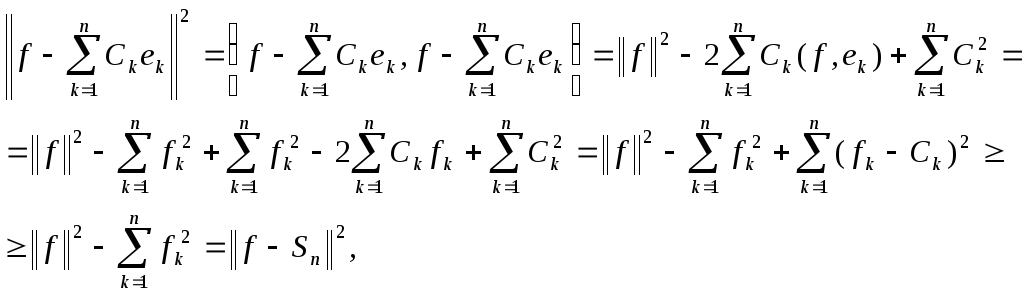
согласно равенству Бесселя. Теорема доказана.
Замечание 4.2. Неравенство (9.2)
называется минимальным свойством
коэффициентов Фурье. Оно означает, что
частичные суммы ряда Фурье![]() наилучшим образом приближают в среднем
элемент
наилучшим образом приближают в среднем
элемент![]() в линейной оболочке первых
в линейной оболочке первых![]() векторов системы (1.2).
векторов системы (1.2).
Определение 5.2.Система
векторов (1.2) называется замкнутой в
нормированном пространстве Е, если![]() и
и![]() существует конечный набор чисел
существует конечный набор чисел![]() такой, что
такой, что
![]() .
(10.2)
.
(10.2)
Если через
![]() обозначить замыкание по норме Е множества
всех конечных линейных комбинаций
системы (1.2) (линейной оболочки
обозначить замыкание по норме Е множества
всех конечных линейных комбинаций
системы (1.2) (линейной оболочки![]() ),
то определение (5.2) можно переформулировать
так: система
),
то определение (5.2) можно переформулировать
так: система![]() замкнута в Е, если Е
замкнута в Е, если Е![]() .
.
Следующие теоремы описывают свойства замкнутых систем.
Теорема 4.2. Если (1.2) ортонормированная система в евклидовом пространстве Е, то следующие условия эквивалентны:
1. Система (1.2) замкнута в Е;
Для
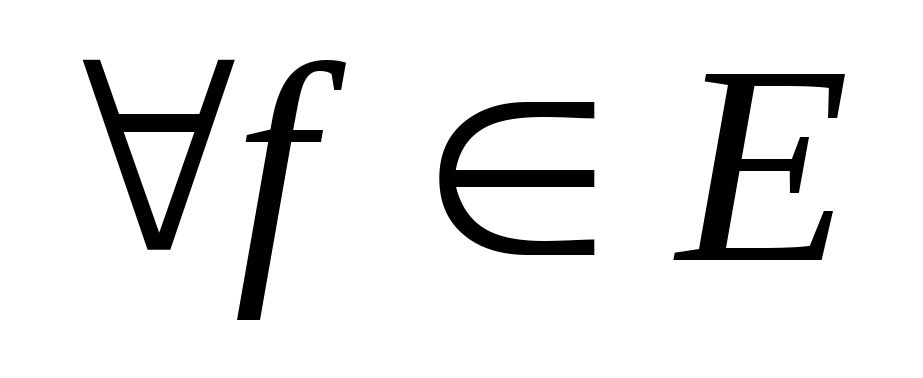 неравенство Бесселя превращается в
неравенство (Парсеваля)
неравенство Бесселя превращается в
неравенство (Парсеваля)
![]() где
где![]() (11.2)
(11.2)
Для
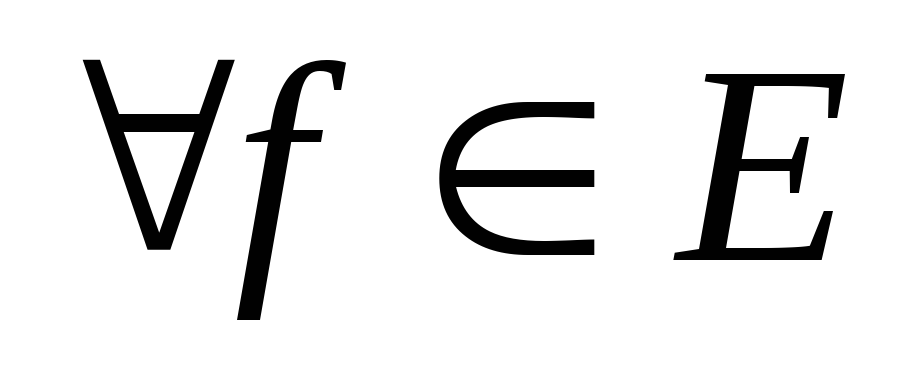 ряд Фурье элемента
ряд Фурье элемента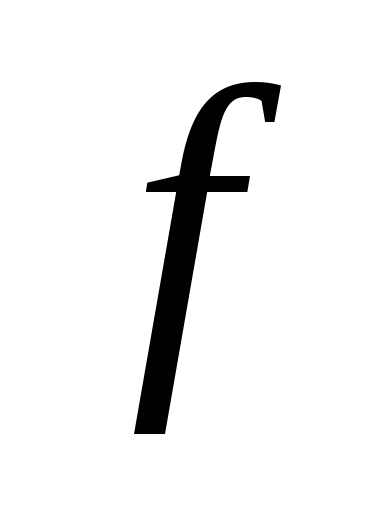 сходится в среднем к
сходится в среднем к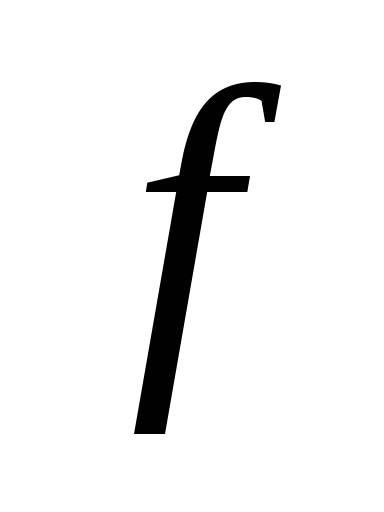 ,
то есть
,
то есть
![]() в среднем. (12.2)
в среднем. (12.2)
Доказательство.
1.![]() 2.
Возьмем
2.
Возьмем![]() и
и![]() .
Так как система (1.2) замкнута, то
.
Так как система (1.2) замкнута, то![]() такие, что
такие, что![]() .
.
Используя равенство Бесселя, и минимальное свойство коэффициентов ряда Фурье (9.2), выведем:
![]()
Если в этом неравенстве перейти к пределу
при
![]() и воспользоваться неравенством Бесселя,
то получим
и воспользоваться неравенством Бесселя,
то получим
![]()
Отсюда следует равенство Парсеваля (11.2).
2.![]() 3.
Для
3.
Для![]() ,
воспользовавшись равенством Парсеваля,
получим
,
воспользовавшись равенством Парсеваля,
получим
![]()
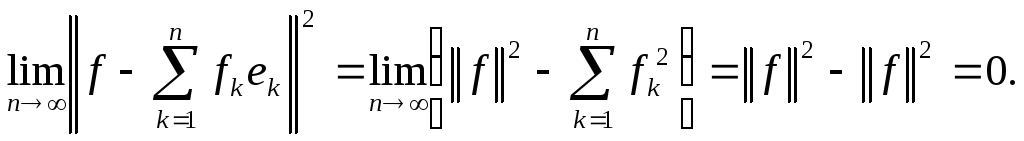
А это и означает (12.2).
3.![]() 1.
Из (12.2) следует
1.
Из (12.2) следует
![]()
Поэтому система (1.2) замкнута. Теорема доказана.
Замечание 5.2. Из теоремы 4.2 следует, что замкнутая ортонормированная система в бесконечномерном пространстве.
Задача 2.2. Если (1.2) есть замкнутая
ортонормированная система в евклидовом
пространстве![]() ,
то
,
то![]() имеет место равенство (обобщённое
равенство Парсеваля)
имеет место равенство (обобщённое
равенство Парсеваля)![]() где
где![]()
![]() есть коэффициенты Фурье элементов
есть коэффициенты Фурье элементов![]() и
и![]() соответственно.
соответственно.
Утверждение 2.2.Если (1.2)
замкнутая ортонормированная система
в![]() ,
то в
,
то в![]() не
существует ненулевого элемента, у
которого все коэффициенты Фурье равны
0. (системы с таким свойством называются
полными).
не
существует ненулевого элемента, у
которого все коэффициенты Фурье равны
0. (системы с таким свойством называются
полными).
Доказательство.
Действительно, если
![]() при всех
при всех![]() ,
то из равенства Парсеваля следует
,
то из равенства Парсеваля следует![]() .
Утверждение доказано.
.
Утверждение доказано.
Следствие 1.2.Для всякой замкнутой
ортонормированной системы в![]() два различных элемента не могут иметь
одинаковые ряды Фурье.
два различных элемента не могут иметь
одинаковые ряды Фурье.
Действительно, если элементы
![]() и
и![]() имеют одинаковые ряды Фурье, то у разности
имеют одинаковые ряды Фурье, то у разности![]() все коэффициенты Фурье равны 0.
Следовательно,
все коэффициенты Фурье равны 0.
Следовательно,![]() .
.
Следствие 2.2. Если (1.2) есть
замкнутая ортонормированная система
в![]() и для элемента
и для элемента![]() в смысле сходимости в среднем имеет
место равенство
в смысле сходимости в среднем имеет
место равенство![]() ,
то
,
то![]() есть коэффициенты Фурье функции
есть коэффициенты Фурье функции![]() ,
то есть
,
то есть![]() .
.
Доказательство.
Пусть
![]() есть коэффициенты Фурье
есть коэффициенты Фурье![]() .
Тогда из условия и утвержденияIIIтеоремы 4.2 следует:
.
Тогда из условия и утвержденияIIIтеоремы 4.2 следует: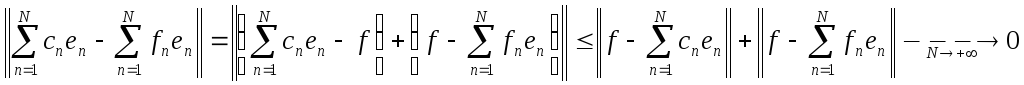 .
Учитывая ортонормированность системы
(1.2), отсюда выведем
.
Учитывая ортонормированность системы
(1.2), отсюда выведем![]() .
Это означает, что
.
Это означает, что![]() и
и![]()
![]() .
Следствие доказано.
.
Следствие доказано.
Мы рассмотрели вопрос о разложении векторов в ряд Фурье в произвольном бесконечномерном Евклидовом пространстве. Ряды Фурье являются эффективным аппаратом при решении различных задач математической физики и математики. При этом в качестве евклидовых пространств берутся функциональные пространства с соответствующими ортонормированными системами. Примерами таких систем являются полиномы Лежандра, полиномы Чебышева, система Хаара, система Радемахера, функция Бесселя и другие.
В следующем параграфе мы подробно рассмотрим вопрос о разложении функций в ряд Фурье по тригонометрической системе.
