§3. Тригонометрический ряд Фурье.

1. Замкнутость тригонометрической системы.

Рассмотрим в пространстве кусочно-непрерывных функций ортонормированную систему (3.2). Скалярное произведение в пространствезадается формулой (5.1).

Определение 1.1. Тригонометрическим многочленом называют выражение вида, где,, …,,, …,произвольные действительные числа.

Доказательство замкнутости тригонометрической системы опирается на следующую теорему Вейерштрасса:

Теорема 1.3.Любую непрерывную на отрезкефункциютакую, что(т.е.) можно равномерно приблизить тригонометрическими многочленами, то естьтакой, что.

Теорема 2.3. Тригонометрическая система (3.2) замкнута в.

Доказательство теоремы опирается на следующие вспомогательные утверждения.

Лемма 1.3.Для любой интегрируемой по Риману на отрезкефункцииинайдется кусочно-постоянная нафункцияпринимающая конечное число значений и такая, что

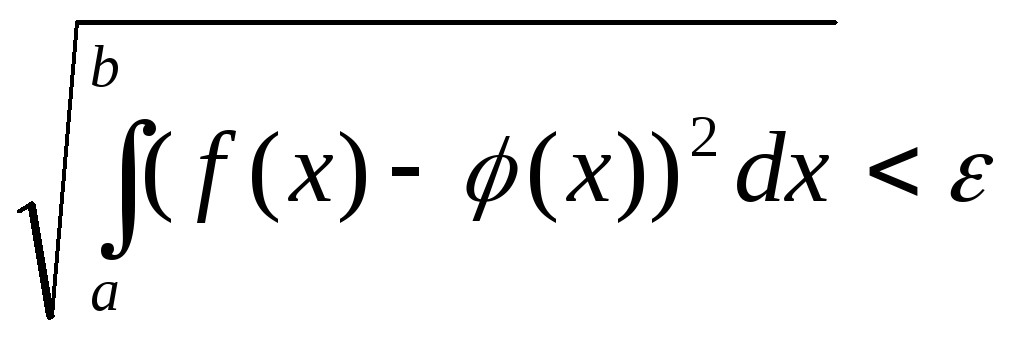
(1.3)

Лемма 2.3.Для любой функции, принимающей конечное число значений, инайдется функциятакая, что

(2.3)

Доказательство леммы 1.3.

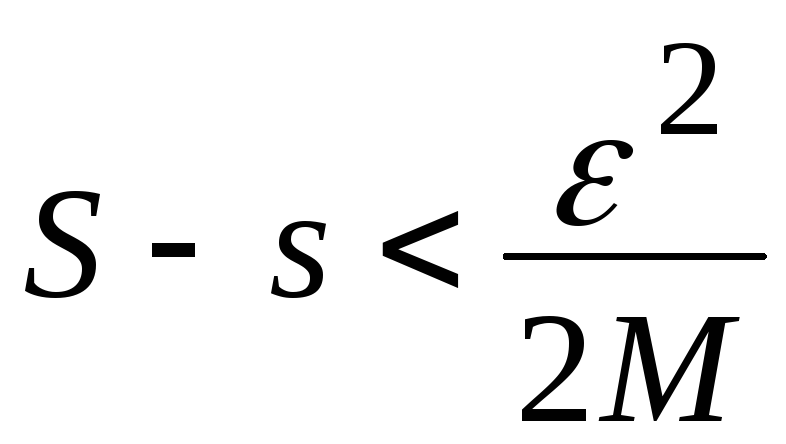Возьмем любую интегрируемую на отрезке функциюи. Из интегрируемости вытекает ограниченность. Пусть. Из критерия интегрируемости следует, что найдется разбиение отрезкаточками,, …,такое, чтои, где,верхняя и нижняя суммы Дарбу соответственно. Здесь,,. Определим функцию

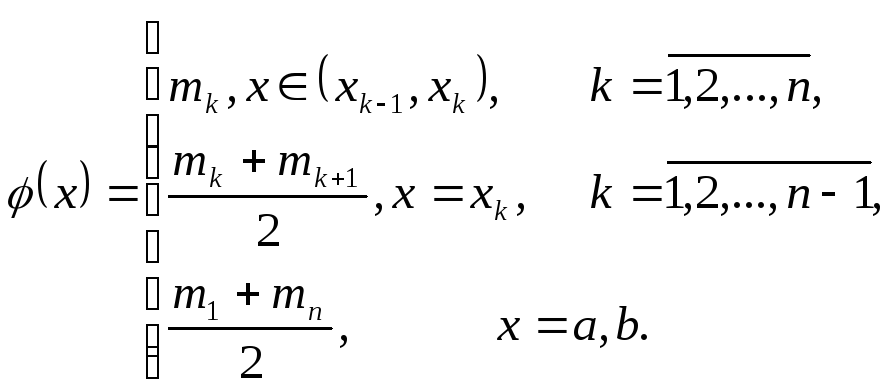
Очевидно, что и принимает конечное число значений. Найдем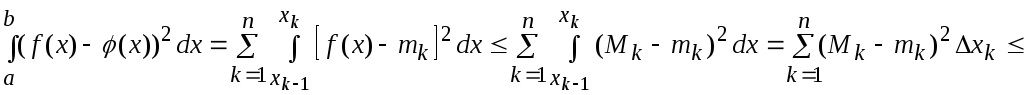

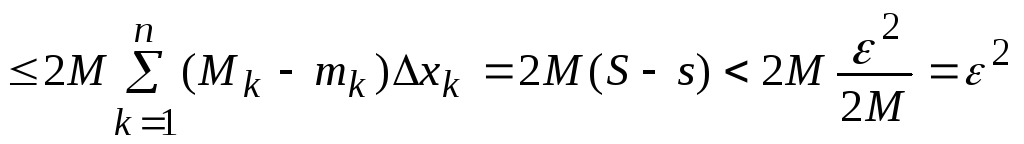. Лемма 1.3 доказана.

Доказательство леммы 2.3.

Пусть функция и принимает конечное число значений. Возьмем. Пусть,, …,все точки разрыва функциина интервале. Обозначим,. Выберем число, где,. Определим функцию

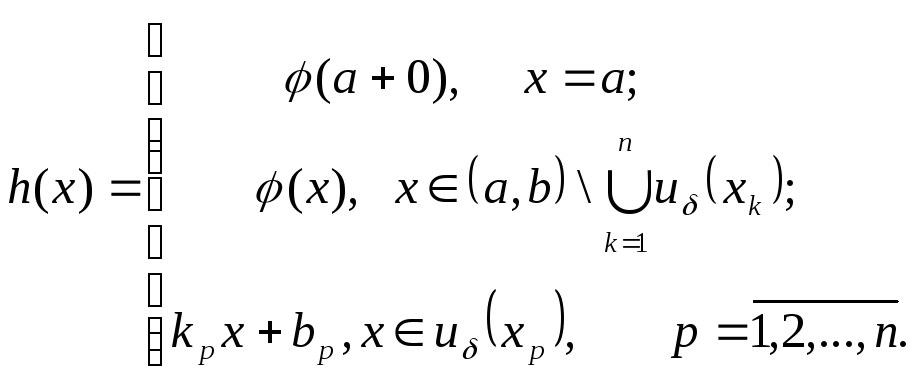
Здесь коэффициенты ,подобраны так, что прямаяприпроходит через точки, а причерез точки

Обозначим . Оценим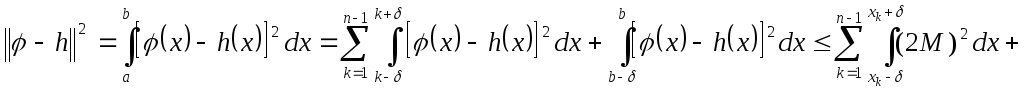

.

Подберем так, чтобы дополнительно выполнялось неравенствоТогдаЛемма доказана.

Доказательство теоремы 2.3.

Возьмем и. Функцияинтегрируема на отрезке, так как ограничена и имеет конечное число точек разрыва. Тогда из леммы 1.3 следует, что найдется кусочно-постоянная функция, принимающая конечное число значений и такая, чтоСогласно лемме 2.3 существует функциятакая, чтоА из теоремы Вейерштрасса вытекает существование тригонометрического многочленатакого, чтоТогдаПоэтомуТеорема доказана.

Следствие 1.3.Тригонометрическая система (4.2) замкнута в пространстве

Доказательство.

Возьмем и. Тогда функцияи согласно теореме 2.3 существует тригонометрический многочлентакой, что.

Поэтому

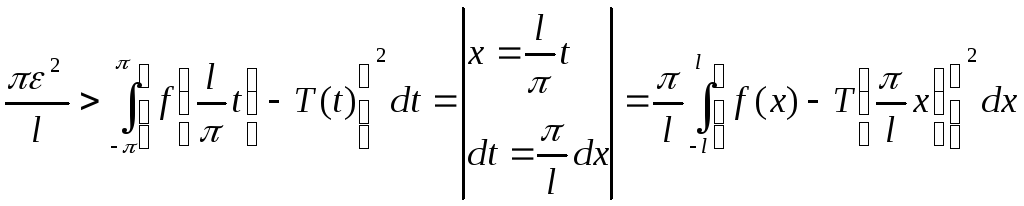
и, следовательно, , что завершает доказательство, поскольку тригонометрический многочленравен линейной комбинацией функций из системы 4.2.

2. Тригонометрическая система в пространстве интегрируемых функций.

Обозначим через множество функций, интегрируемых по Риману на отрезке. Множество- линейное пространство. Это вытекает из линейных свойств интеграла Римана. Если попытаться ввести вскалярное произведение по формуле (5.1), то первая аксиома скалярного произведения не выполнится. Действительно, для функциивезде на, кроме быть может, множества меры 0. Напомним, что числовое множество имеет меру 0, еслисуществует конечная или счетная система интервалов, суммарная длина которых меньше, а объединение содержит данное множество. Таким образом,может не равняться тождественно 0.

Определение 1.3.Говорят, что некоторое свойство справедливо почти всюду на отрезке, если оно выполнено для всех точек, кроме, быть может, множества меры 0.

Будем говорить, что две функции иэквивалентны и писать~, если они равны почти всюду на отрезке.

Легко проверить, что это действительно отношение эквивалентности. Поэтому множество интегрируемых функций разбивается на непересекающиеся классы по отношению эквивалентности.

Обозначим через множество классов эквивалентных, то есть равных почти всюду функций из.

Стандартным образом в вводится структура линейного пространства. Каждую функцию из данного класса будем называть представителем этого класса.

Под суммой двух классов из будем считать класс, содержащий сумму двух представителей этих классов.

Для и любого классаопределимкак класс, содержащий произведениена представитель класса.

Задача 1.3.Проверить, что так определенные операции сложения и умножения на число вне зависят от представителей данных классов.

Нулем в пространстве является класс, состоящий из функций равных 0 почти всюду на. Легко проверить ввыполнение всех аксиом линейного пространства.

В дальнейшем, если это не будет вызывать недоразумений, будем обозначать одними и теми же буквами как сами классы из, так и их представителей. А само пространство, как и, будем называть пространством интегрируемых по Риману функций на отрезке.

Определим в скалярное произведение по следующему правилу:

положим

(3.3)

где под интегралом стоит произведение произвольных двух представителей классов Из свойств интеграла Римана следует, что интеграл в формуле (3.3) существует и одинаков для всех представителей классови. Теперь легко проверить выполнение всех аксиом скалярного произведения. Таким образом,является евклидовым пространством со скалярным произведением (3.3). Сходимость по норме, порожденной скалярным произведением (3.3) (т.е.) называется сходимостью в среднем.

Очевидно, что тригонометрическая система (3.2) (точнее, система классов функций эквивалентных функциям из (3.2)) является ортонормированной системой в .

Теорема 3.3.Тригонометрическая система (3.2) замкнута в пространстве.

Доказательство теоремы 3.3 полностью повторяет доказательство теоремы 2.3 поскольку лемма 1.3 доказана нами для функций из . Если в доказательстве следствия 1.3 заменить пространство, на пространство, то получим доказательство следующего следствия из теоремы 3.3.

Следствие 2.3.Тригонометрическая система (4.2) замкнута в пространстве.

Из замкнутости тригонометрической системы (4.2) и теоремы 4.2 следует, что для функции либо из пространства, либо изряд Фурье сходится кв среднем и имеет место равенство Парсеваля.