3. Ряд Фурье по тригонометрической системе (3.2).

Возьмем произвольную функцию и напишем ее ряд Фурье по системе 3.2. Согласно определения 3.2 найдем сначала коэффициенты Фурье:

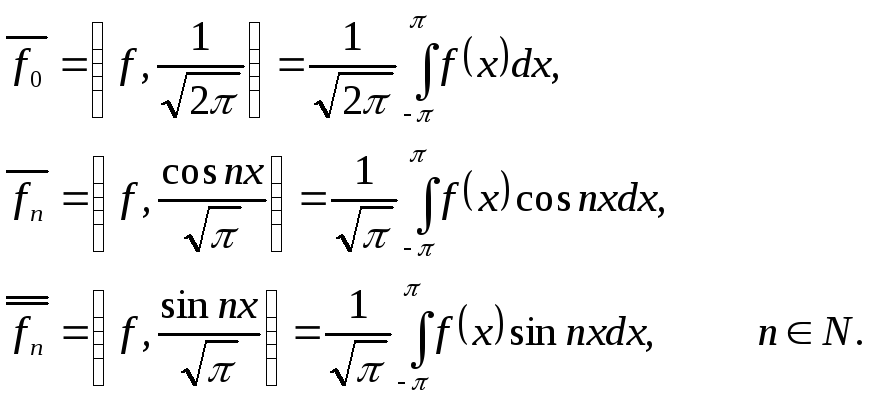
Из замкнутости тригонометрической системы в и теоремы 4.2 следуют равенства:

(4.3)

и

Последнее равенство представляет собой равенство Парсеваля. Отметим, что согласно теоремы 4.2 пока мы можем утверждать, что ряд Фурье (4.3) сходится в среднем, то есть по норме пространства . В следующем параграфе мы рассмотрим вопрос о поточечной и равномерной сходимости ряда Фурье.

Запишем тригонометрический ряд Фурье в общепринятой форме:

(5.3)

где

(6.3)

,

Отметим, что из замечания 3.2 следует, что и. Равенство Парсеваля примет вид:

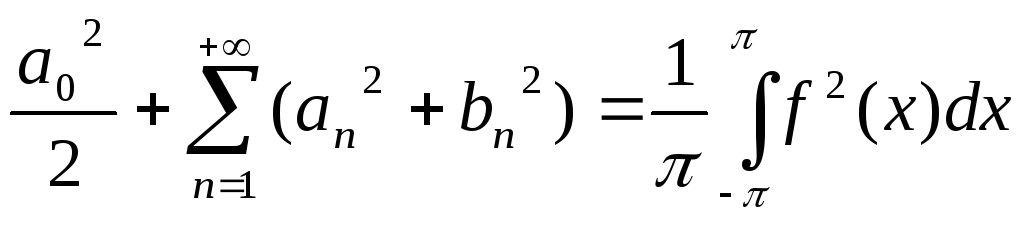(7.3)

4.Тригонометрический ряд Фурье в пространстве .

Ряд Фурье по ортонормированной системе (4.2) для функции согласно теореме 4.2 и следствия 1.3 также сходится кв среднем и имеет вид:

где

Обозначим:

,

, (8.3)

Тогда ряд Фурье и равенство Парсеваля примут вид:

(9.3)

(10.3)

Равенства (7.3), (10.3) называются также равенствами Ляпунова.

Пример 1.3:разложить в тригонометрический ряд Фурье функцию:

и написать равенство Ляпунова.

Для вычисления коэффициентов Фурье в этом и последующих примерах будем применять следующие формулы:

; (11.3)

; (12.3)

; (13.3)

; (14.3)

; (11.3’)

; (12.3’)

; (13.3’)

; (14.3’)

Эти соотношения легко выводятся интегрированием по частям.

Очевидно, что в примере 1.3 . Используя формулы (6.3), (11.3), (12.3), найдем коэффициенты Фурье:

;

.

Следовательно, ряд Фурье имеет вид:

(15.3)

Пока мы можем только утверждать (согласно теореме 4.2), что этот ряд сходится к в среднем. В следующем параграфе мы вернемся к этому примеру и покажем, что этот ряд Фурье сходится кпоточечно на интервале, а в точкахего сумма равна.

Чтобы написать равенство Ляпунова найдем

.

Тогда согласно (7.3) равенство Ляпунова имеет вид:

.

5. Ряд Фурье чётных и нечётных функций. Разложение в ряд по синусам или косинусам.

Вычисление коэффициентов ряда Фурье значительно упрощается в случае четной или нечетной функции. При этом нам понадобятся следующие вспомогательные утверждения.

Утверждение 1.3:Еслии нечетная, то.

Доказательство:

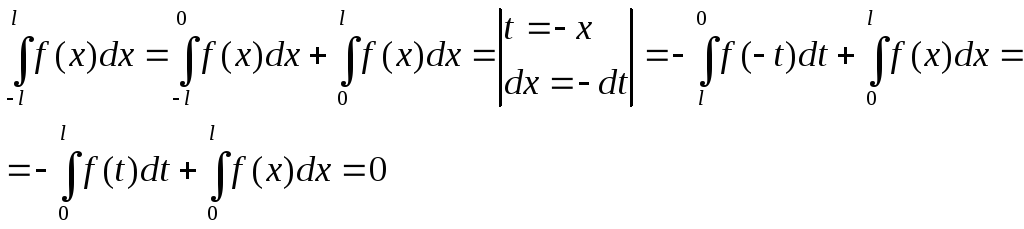
Утверждение доказано.

Утверждение 2.3:Еслии четная, то.

Доказывается это утверждение точно так же, как и предыдущее.

Если в ряд Фурье по системе (4.2) раскладывается нечетная функция

, то- нечетная функция, а- четная и из утверждений 1.3, 2.3 и формулы (8.3) получим:

(16.3)

(17.3)

Поэтому ряд Фурье имеет вид:

(18.3)

Говорят, что нечетная функция раскладывается в ряд Фурье « по синусам».

Если в ряд Фурье раскладывается четная функция , то

- также четная функция, а- нечетная функция и, следовательно

(19.3)

(20.3)

(21.3)

(22.3)

В этом случае говорят, что четная функция раскладывается в ряд Фурье «по косинусам». Отметим, что согласно теореме 4.2 ряды Фурье (18.3), (22.3) сходятся к в среднем.

Формулы (17.3)-(22.3) несколько упростятся, если .

Если - нечетная функция, то для нее

(23.3)

(24.3)

(25.3)

Если - четная функция, то для нее

(26.3)

(27.3)

(28.3)

Опираясь на формулы (16.3)-(22.3), докажем теорему, которая используется при решении многих краевых задач математической физики.

Теорема 4.3:Система функций

(29.3)

является замкнутой ортонормированной системой в пространстве .

Для любой функции коэффициенты Фурье по системе (29.3) определяются формулой (17.3), а ряд Фурье представляется формулой (18.3) и сходится кв среднем в пространстве.

Доказательство:

Ортонормированность системы (29.3) на отрезке проверяется непосредственным интегрированием. (Задача 1.3:Доказать, что система (29.3) ортонормированна в). Докажем замкнутость.

Возьмем произвольную функцию и. Продолжимна отрезокнечетным образом и обозначим черезпродолженную функцию. Таким образом,

Очевидно, что . Так какнечетная функция, то ее коэффициенты Фурье можно вычислить по формулам (16.3), (17.3). Обозначим через-n-ю частичную сумму ряда Фурье функции. Из следствия 1.3 и теоремы 4.2 следует, что.

Следовательно, такое, что. Отсюда, воспользовавшись четностью функции, утверждением 3.2 и теоремой 1.2, получим:

Поэтому . Из этого неравенства и того факта, чтопредставляет собой конечную линейную комбинацию функций из системы (29.3), вытекает замкнутость системы (29.3) в.

Последнее утверждение этой теоремы является следствием простых выкладок и теоремы 4.2. Теорема доказана.

Положив , получим следующее:

Следствие 3.3:Тригонометрическая система

(30.3)

является ортонормированной и замкнутой системой в пространстве . Для любой функциикоэффициенты Фурье по системе (30.3) определяются формулами (24.3), а ряд Фурье представляется формулой (25.3) и сходится кв среднем в.

Точно так же, только с использованием четного продолжения функции , доказывается

Теорема 5.3:Система функций

(31.3)

является ортонормированной и замкнутой системой в пространстве . Для любой функциикоэффициенты Фурье по системе (31.3) вычисляются по формулам (19.3),(20.3), а ряд Фурье представляется формулой (22.3) и сходится кв среднем в пространстве.

При получим

Следствие 4.3. Тригонометрическая система

(32.3)

является ортонормированной и замкнутой системой в пространстве . Длякоэффициенты Фурье вычисляются по формулам (26.3), а ряд Фурье представляется формулой (28.3) и сходится кв среднем в.

Замечание 1.3.Если в задаче требуется разложить функциюна отрезкелибо по синусам либо по косинусам, это означает, что необходимо разложитьв ряд Фурье на отрезкелибо по ортонормированной системе (29.3), либо по системе (31.3). При этом можно воспользоваться формулами (17.3), (18.3), либо (19.3).(20.3), (22.3) соответственно. В случаеможно использовать формулы (24.3), (25.3), либо (26,3), (28,3).

Задача 2.3. Проверить, чторавенство Ляпунова(Парсеваля) по системе (30.3) примет вид

и, что равенство Ляпунова (Парсеваля) по системе (32.3) примет вид .

Написать равенство Парсеваля для функции по системе (29.3) и (31.3).

Пример 2.3. Разложитьв ряд Фурье на отрезкеи написать равенство Ляпунова.

Очевидно, что и является четной. Положиви воспользовавшись формулами (12.3),(19.3)-(22.3), получим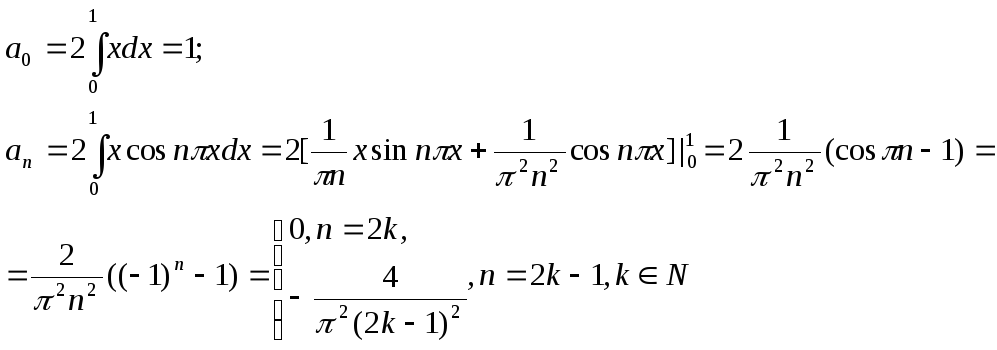

. Ряд Фурье имеет вид:

. (33.3)

Найдем также .

Поэтому равенство Ляпунова имеет вид

Отметим, что ряд (33.3) сходится не только в среднем, но и равномерно. Действительно, общий член ряда (33.3) по модуля не превосходит , а числовой рядсходится. Поэтому по признаку Веерштрасса ряд (33.3) сходится на отрезкеравномерно к некоторой сумме(непрерывностьвытекает из равномерной сходимости и непрерывности всех слагаемых ряда (33.3)). А из равномерной сходимости вытекает сходимость в среднем (см. задачу 1.1). Следовательно, ряд (33.3) сходится в среднем ки к. Поэтомупочти всюду на. Но так как,, тона. Поэтому ряд Фурье функциисходится к ней равномерно на отрезке.

Отметим, что в следующем параграфе мы научимся более быстро по виду только функции исследовать вопрос о поточечной и равномерной сходимости ряда Фурье функции.

Если в равенстве (33.3) положить , то получим

Зная эту сумму не трудно найти сумму

Отсюда , то есть. Это равенство впервые получил Эйлер.

Пример 3.3. Разложить функциюна отрезкепо синусам.

Требуется разложить данную функцию по тригонометрической системе (30.3). Согласно следствию 3.3 коэффициенты Фурье найдем по формуле (24.3) используя равенство (13.3): Тогда согласно формуле (25.3). (34.3)

Согласно следствию 3.3 данный ряд сходится к функции в среднем. В следующем параграфе мы вернемся к этому примеру, чтобы исследовать вопрос о поточечной сходимости.