Комплексная форма записи тригонометрического ряда Фурье.

Возьмем произвольную функцию . Согласно теоремам (4.2) и (3.3) ее ряд Фурье по системе (3.2) сходится к ней в среднем. Существует более компактная комплексная форма записи тригонометрического ряда Фурье. Для ее получения выразим по формулам Эйлера

.

Рассмотрим ряд Фурье (5.3) функции и будем называтьn-й частичной суммой ряда Фурье выражение, (35.3) где коэффициентывычисляются по формулам (6.3).

Выразив ипо формулам Эйлера и подставив их в, получим:

Если обозначить

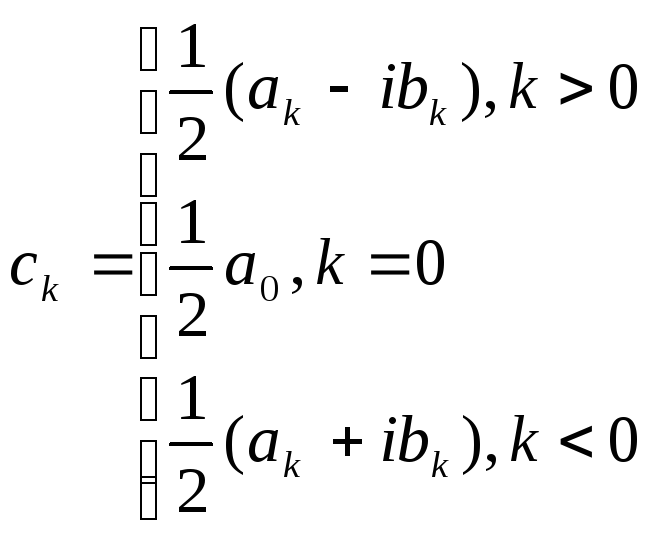
то перепишется так:

(36.3)

Легко видеть, что

(37.3)

Тогда сам ряд Фурье можно переписать так:

(38.3)

Следует только помнить, что суммирование ряда (38.3) понимается в смысле сходимости в среднем симметричных сумм (36.3).

Определение 2.3.Ряд (38.3) с коэффициентами (37.3) называется рядом Фурье функциив комплексной форме.

Отметим еще, что непосредственно из определения вытекает следующее свойство:

(39.3)

Легко видеть, что условие (39.3) является необходимым и достаточным условием того, что сумма принимает только действительные значения.

Замечание 1.3.Точно также можно показать, что ряд Фурье функциипо системе (4.2) в комплексной форме имеет вид:

, где

Замечание 2.3Рассмотрим более широкий класс функций, чем. Обозначим черезмножество классов эквивалентных (то есть равных почти всюду на) функций, имеющих нане более чем конечное число особых точек и таких, что их квадрат модуля интегрируем напо Риману в собственном или несобственном смысле. Очевидно, что. Скалярное произведение втакже определим формулой (5.1).

Не трудно проверить, что все определения и теоремы останутся в силе, если в формулировках пространство заменить на. В частности, справедлива теорема о том, что система (4.2) замкнута в пространстве.

§ 4. Поточечная и равномерная сходимость тригонометрического ряда Фурье

В предыдущем параграфе в теореме 3.3 и следствии 2.3 доказана сходимость тригонометрического ряда Фурье (9.3) в среднем, то есть по норме пространства I[-l,l]. При решении многих задач математической физики с помощью рядов Фурье важную роль играет вопрос о поточечной и равномерной сходимости ряда Фурье, так как он напрямую связан с вопросом существования классического решения. Известно, что для поточечной сходимости ряда Фурье (а тем более равномерной) недостаточно требовать только непрерывности функции. В этом параграфе будут рассмотрены дополнительные условия на функцию, достаточные для поточечной и равномерной сходимости тригонометрического ряда Фурье. Но вначале докажем несколько вспомогательных теорем и тождеств.

1. Свойства интегрируемых функций

Лемма 1.4.Предположим, что

1. Функция 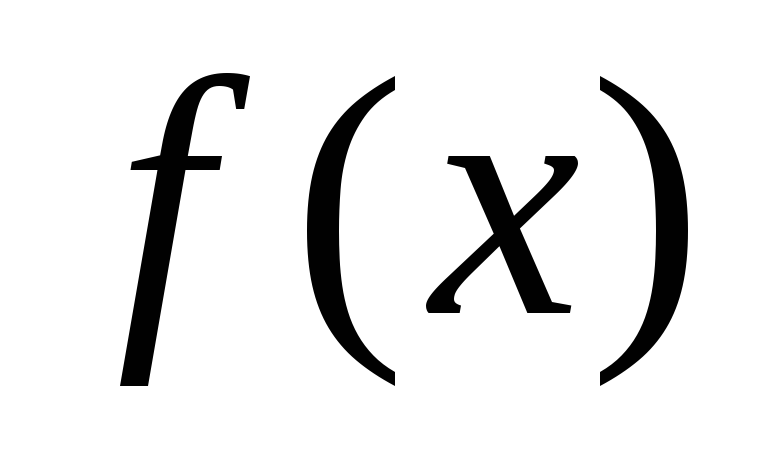определена и ограничена на промежутке;

2. 

Тогда

Доказательство.

Доопределим , положив. Из условия 1) следует, что существуеттакая, чтоПроверим выполнение критерия интегрируемостина. Для этого обозначим через ,верхнюю и нижнюю сумму Дарбу функциина отрезкедля данного разбиенияTсоответственно.

Возьмем . Выберем точкутак, чтобы

Из условия 2) следует, что существует разбиение отрезкатакое, что. Обозначим черезT-разбиение отрезка [a,b]. Тогда. Критерий интегрируемости выполнен. Лемма доказана.

Лемма Римана. Если, то

(1.4)

(2.4)

Доказательство.

Докажем предел (1.4). Сначала заметим, что (3.4)

Пусть Tразбиение [a,b] точками. Обозначим,k=1,…,n. Преобразуем

Отсюда и (3.4), используя несложные оценки, получим

(4.4)

Берем Так как то существует разбиениеTтакое, чтоЗафиксируем это разбиение. Обозначим через. Тогда для любого из (4.4) получим.

Предел (1.4) доказан по определению. Предел (2.4) доказывается аналогично. Лемма доказана.

Следствие 1.4.Пустьf(x) определена на промежутке (a,b] (либо на [a,c)).

Если для любогоf(x) не ограничена в правой окрестности точкиа(левой окрестности точкиb) и несобственный интеграл второго родасходится абсолютно, то равенства (1.4) и (2.4) также выполнены, только слева в этих равенствах берутся несобственные интегралы второго рода.

Доказательство

Берем . Так как, тотакое, что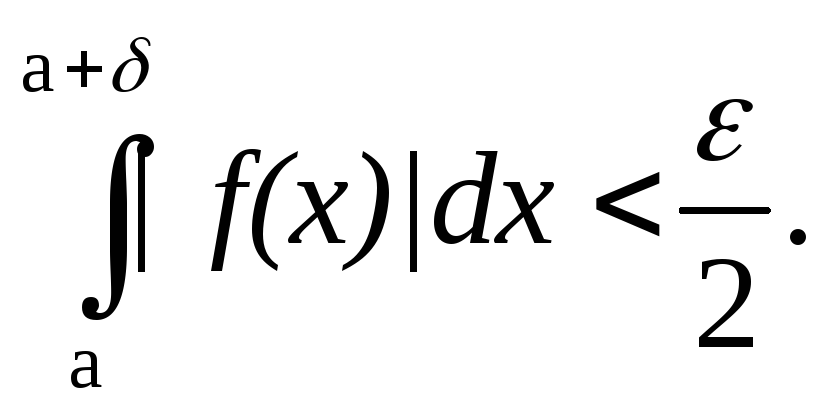Поскольку по условиюто согласно теореме Римана существуеттакое, что для любого выполнено. СледовательноПредел (1.4) доказан. Предел (2.4) доказывается точно также. Еслиfимеет особенность в точкеb, то следствие доказывается аналогично. Следствие доказано.