2. Интегральное представление частичных сумм тригонометрического ряда Фурье

Возьмем функцию Продолжим функциюf на всю числовую прямую периодически с периодом 2и полученную таким образом 2- периодическую функцию будем также обозначатьf.

Пусть n-я частичная сумма ряда Фурье, определенная формулой (35.3). Заметим, что если на, то

. (5.4)

Действительно, в этом случае , а остальныекоэффициенты Фурье равны 0.

В следующей лемме будет получена более компактная форма записи для , которая облегчит исследование поточечной сходимости этой последовательности.

Лемма 2.4. Пустьи 2периодична. Тогда

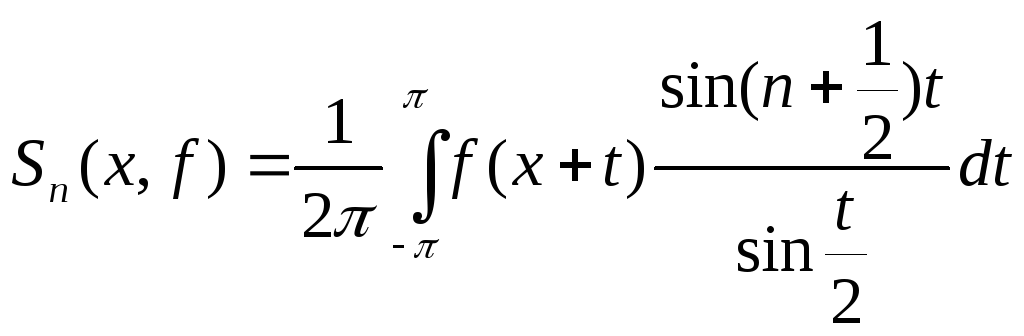(6.4)

Доказательство.

Сначала заметим, что если функцию

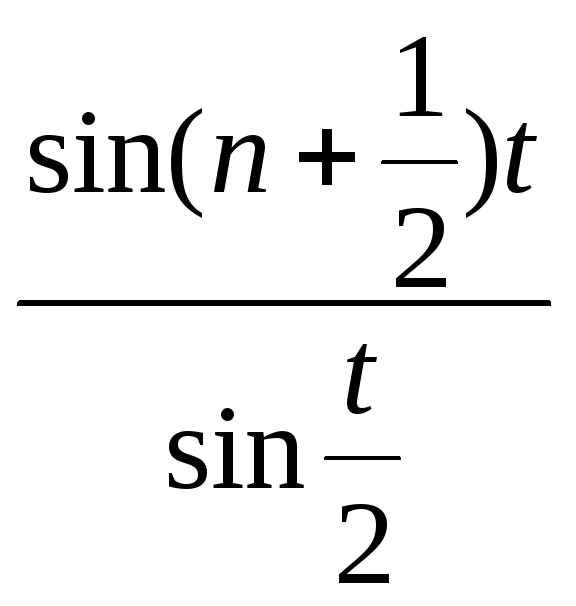(7.4)

доопределить в 0 ее предельным значением равным (2n+1), то получим непрерывную функцию на отрезке. Отсюда, а также теоремы 1.2 и условия леммы следует существование собственного интеграла Римана в (6.4).

Для доказательства леммы будем использовать следующее тождество:

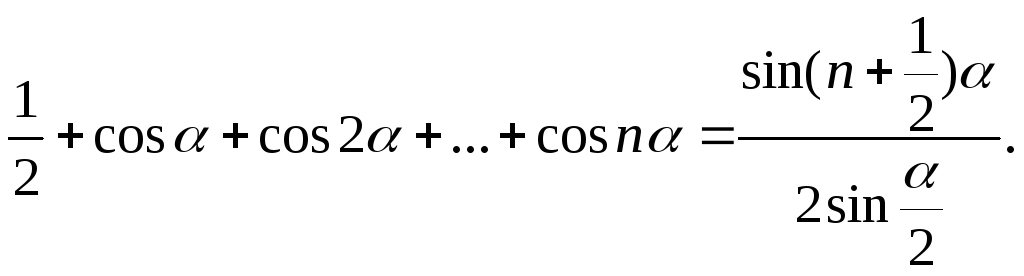(8.4)

Это тождество справедливо при всех , если приправую часть заменить ее предельным значением равным

Формула (8.4) получится, если левую часть умножить и разделить на и проделать несложные преобразования.

Подставив в (35.3) вместо выражения из формул (6.3) и воспользовавшись (8.4), получим

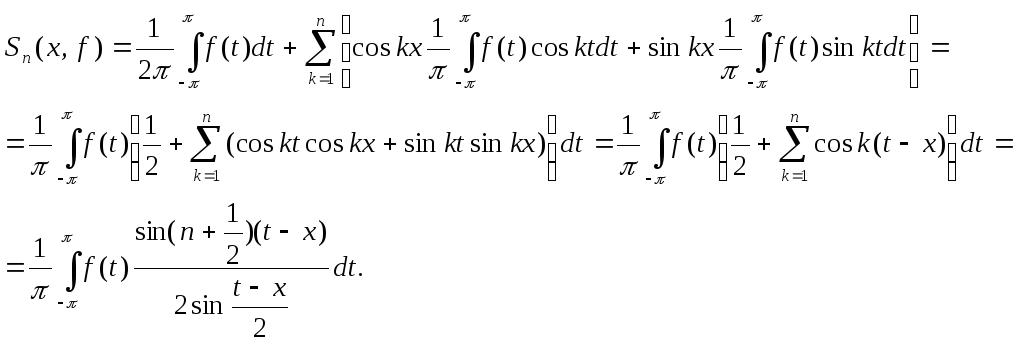
Сделаем линейную заменуи воспользуемся утверждением 2.2:

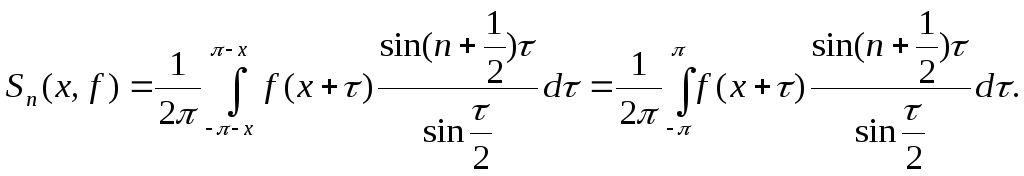
Лемма доказана.

Следствие 1.4.Если в тождество 6.4 подставитьи воспользоваться 5.4, то получим

(9.4)

Определение 1.4.Функция (7.4) называется ядром Дирихле, а правая часть равенства (6.4) называется интегралом Дирихле.

График ядра Дирихле изображен для n=5,6 изображен на рисунке 3.

3. Необходимое и достаточное условие сходимости ряда Фурье в точке

Докажем основную теорему этого параграфа.

Теорема 1.4.Пустьи 2периодична. Для того чтобы в точкехсуществовал

(10.4)

необходимо и достаточно, чтобы такое, что

(11.4)

Здесь

(12.4)

Доказательство.

Для сокращения записи обозначим

Сначала, воспользовавшись формулами (6.4), (9.4), преобразуем разность

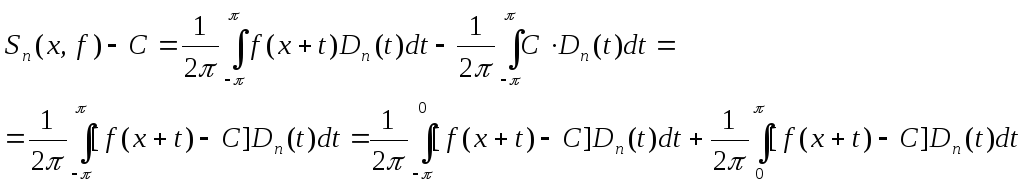
Сделаем в первом интеграле замену переменной

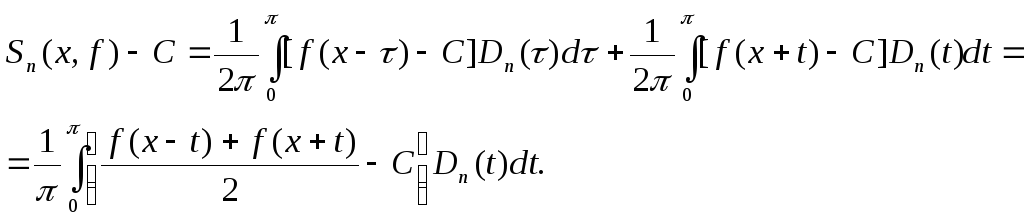
Возьмем Воспользовавшись обозначением (12.4), получим:

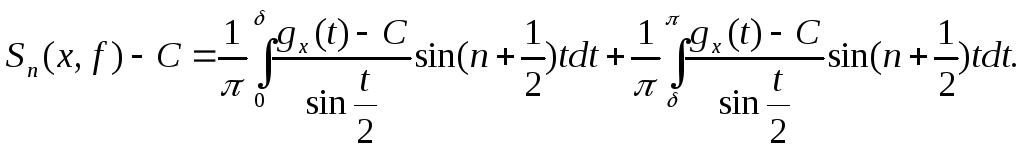(13.4)

Обозначим первый и второй интегралы в (13.4) через иI₂ соответственно.

Тогда

;

Отметим сразу, что непрерывна на. Поэтому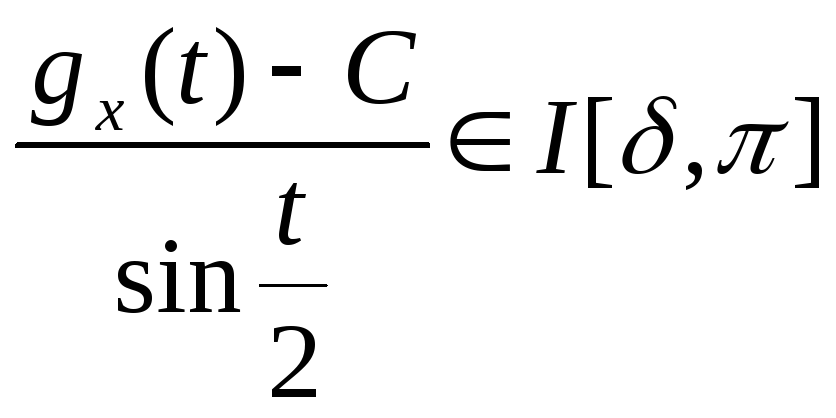и по лемме Римана

Для доказательства леммы осталось проверить, что тогда и только тогда, когда выполнено условие (11.4). Сначала, воспользовавшись асимптотическими формулами, найдем

.

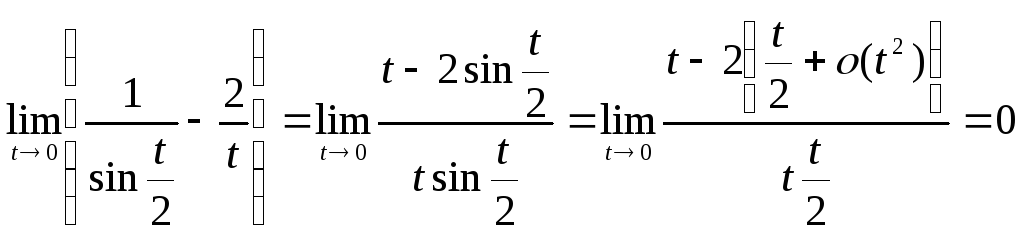Отсюда следует, что функция непрерывна и ограничена на. Поэтому, согласно лемме 1.4,. Проделав несложные выкладки, преобразуем

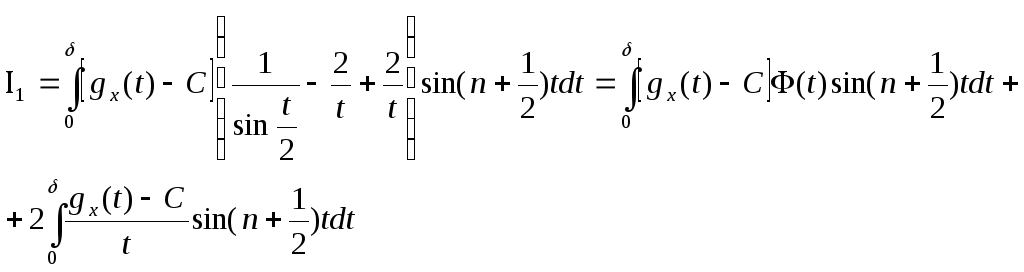
Поскольку , то из леммы Римана следует, что первый интеграл в последнем равенстве стремится к нулю при. Таким образом, существованиеравносильно (11.4). Теорема доказана.

Следствие 2.4:(Принцип локализации)

Пусть функции и существует точкатакая, что, где- окрестность точкитакая, что. Тогда ряды Фурье функцийисходятся или расходятся в точкеодновременно, а в случае сходимости их суммы в точкесовпадают.

Доказательство:

Пусть ряд Фурье функции сходится в точкек значению. Из теоремы 1.4 следует, чтотакое, что справедливо равенство (11.4), где

Подберем такое , что.Функция( или, если). Тогда по лемме Римана. Следовательно,

Но, согласно условия, , поскольку. Поэтому из теоремы 1.4 делаем вывод, что ряд Фурье функциив точкесходится к числу. Аналогично доказывается, что из сходимости ряда Фурье функциив точкек числуследует сходимость кряда Фурье функциив той же точке.

Если ряд Фурье функции в точкерасходится, то ряд Фурье функциив точкетакже расходится, так как в противном случае, по доказанному выше, ряд Фурье функциитакже сходился бы и мы получили бы противоречие. Следствие доказано.

Заметим, что при выполнении условий следствия 2.4 функции имогут иметь различные ряды Фурье, поскольку вне окрестностиони принимают, вообще говоря, различные значения.

Замечание 1.4:Принцип локализации означает, что расходимость или сходимость к некоторомуряда Фурье функциив точкеопределяется значениями функциив сколь угодно малой окрестности точки.

Замечание 2.4:Из доказательства следствия 2.4 видно, что если, то утверждение следствия 2.4 останется в силе, если функцииисовпадают в левой и правой окрестностях точекисоответственно. Действительно, в этом случае достаточно продолжить функцииина всю прямуюRпериодически с периодоми для продленных функций повторить доказательство следствия 2.4.