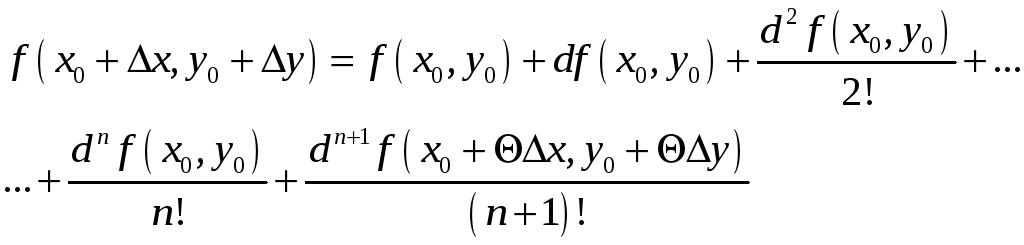частные произв
.doc3. Частные производные и дифференциалы высших порядков
3.1 Частные производные высших порядков
Частные производные
 называют частными
производными первого порядка.
Их можно рассматривать как функции от
называют частными
производными первого порядка.
Их можно рассматривать как функции от
![]() .
Эти функции в свою очередь могут иметь
частные производные, которые называются
частными
производными второго порядка. Они
обозначаются следующим образом:
.
Эти функции в свою очередь могут иметь
частные производные, которые называются
частными
производными второго порядка. Они
обозначаются следующим образом: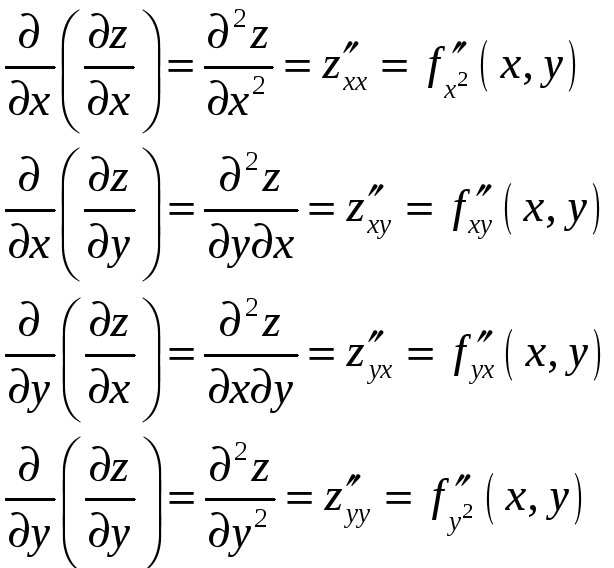 .
.
Аналогично определяются частные производные 2-го и 3-го и т.д. порядков.
Так
 и т.д.
и т.д.
Частная производная второго и более высокого порядка, взятая по различным переменным называется смешанной частной производной
Теорема 2
Смешанные производные
второго порядка равны, если они непрерывны:
![]()
Следствие
Смешанные производные высших порядков равны, если непрерывны и получены по одним и тем же переменным одинаковое число раз, но может быть в разной последовательности.
3.2 Дифференциалы высших порядков
Заметим, что для функции нескольких переменных справедливы те же общие правила дифференцирования, что и для функции одной переменной.
Пусть
![]() ,
тогда
,
тогда
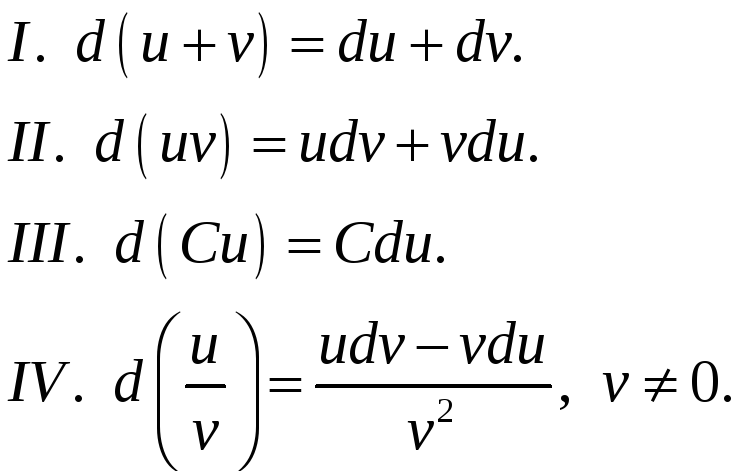
Например, имеем:
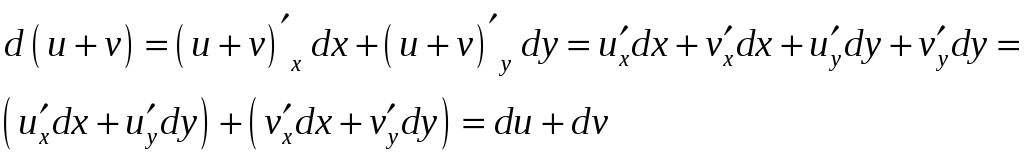
Пусть имеется
функция
![]() независимых
переменных
независимых
переменных
![]() и
и
![]() ,
обладающая непрерывными частными
производными второго порядка. Рассмотрим
её полный дифференциал
,
обладающая непрерывными частными
производными второго порядка. Рассмотрим
её полный дифференциал
 (1)
(1)
(![]() и
и
![]() – произвольные приращения), который
назовем полным
дифференциалом первого порядка
(или, кратко, первым
дифференциалом).
– произвольные приращения), который
назовем полным
дифференциалом первого порядка
(или, кратко, первым
дифференциалом).
Так как
![]() и
и
![]()
![]()
![]() по предположению имеют непрерывные
частные производные первого порядка,
то от функции
по предположению имеют непрерывные
частные производные первого порядка,
то от функции
![]() ,
в свою очередь, можно взять полный
дифференциал
,
в свою очередь, можно взять полный
дифференциал
![]() .
Так получим полный
дифференциал второго порядка
(или кратко второй
дифференциал),
который обозначается
.
Так получим полный
дифференциал второго порядка
(или кратко второй
дифференциал),
который обозначается
![]() .
И т.д.
.
И т.д.
Найдем выражение для второго дифференциала
 (2)
(2)
(здесь
![]() ).
).
Формула (2) обобщается
на случай дифференциала
![]() -го
порядка.
-го
порядка.
3.Формула Тейлора для функции двух переменных
Пусть имеется
функция
![]() независимых
переменных
независимых
переменных
![]() и
и
![]() ,
имеющая непрерывные частные производные
всех порядков до
,
имеющая непрерывные частные производные
всех порядков до
![]() -го
включительно в некоторой окрестности
точки
-го
включительно в некоторой окрестности
точки
![]() .
Пусть точка
.
Пусть точка
![]() принадлежит этой окрестности. Определим
на отрезке
принадлежит этой окрестности. Определим
на отрезке
![]() вспомогательную функцию
вспомогательную функцию
![]() :
:
![]() ,
(3)
,
(3)
где
![]() .
Согласно формуле Тейлора, имеем:
.
Согласно формуле Тейлора, имеем:
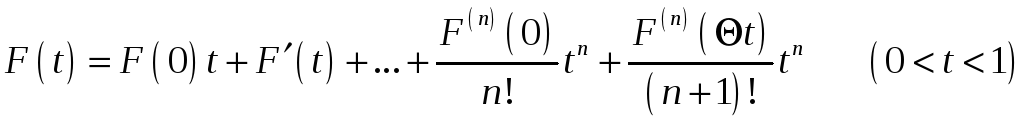 (4)
(4)
Вычислим коэффициенты
формула (4) с помощью равенства (3). При
![]() имеем
имеем
![]() .
Дифференцируя сложную функцию
.
Дифференцируя сложную функцию
![]() по
по
![]() получим:
получим:
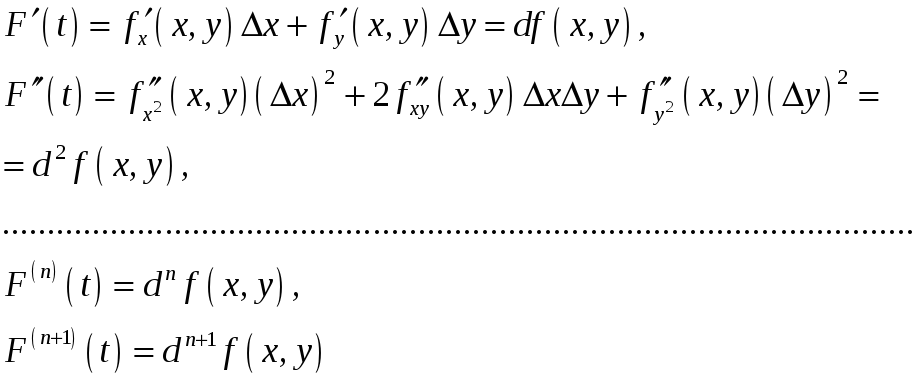 ,
,
Заменив в последнем
равенстве
![]() на
на
![]() ,
а в остальных положим
,
а в остальных положим
![]() ,
найдем:
,
найдем:
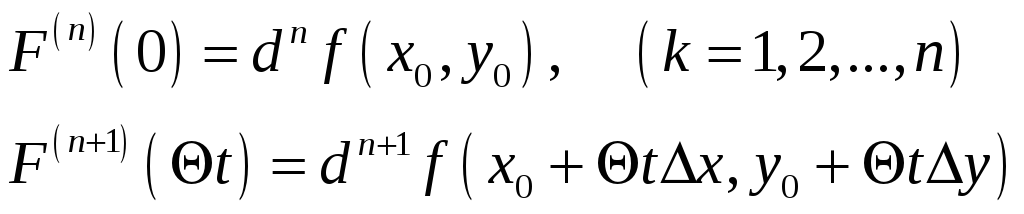
Если подставим
найденные выражения в равенство (4) и
затем положим
![]() ,
то получим для
,
то получим для
![]() формулу Тейлора:
формулу Тейлора: