ГОУВПО «Воронежский государственный технический университет» Факультет энергетики и систем управления Кафедра высшей математики и физико-математического моделирования

Курсовая работа

по дисциплине дискретная математика на тему:

“Разработка схемы управления входным семафором”

Выполнил: студент гр. АТР-131 ___ Косинов Е.А_

Принял: доц. Купцов В. С.

Воронеж 2013 г.

Содержание

Условие задачи…………………………………………………………………………….3

Теоретическое введение…………………………………………………………………..4

Решение…………………………………………………………………………………….?

Заключение……………………………………………………………………………….??

Список литературы………………………………………………………………………??

Условие задачи

Разработать схему управления входным семафором, работающим по следующему правилу:

“Красный свет”- все пути заняты или скорость подхода недопустима высока;

“Желтый свет”- свободный путь есть, но стрелка на этот путь еще не переключена, скорость подхода в норме;

“Зеленый свет”- стрелка переключена на свободный путь, скорость подхода в норме;

Схема установки

X 1 Y1

X2 Y2

X3 Y3

Теоретическое введение

Булева алгебра

Булева алгебра — раздел математики, изучающий логические выражения и операции. Логические выражения представляют собой высказывания — некоторые утверждения, которым всегда можно сопоставить одно из двух логических значений: ложь или истина (их можно обозначать как 0 и 1, F и T, false и true).

Для сравнения, элементарная алгебра занимается арифметическими выражениями и операциями.

Булева алгебра получила свое название в честь своего создателя Джорджа Буля (1854 г.), являющегося одним из предтеч математической логики.

Среди своих прочих приложений, булева алгебра позволяет программистам формулировать сложные условия для применения в условных операторах или операторах цикла, а компьютерам — определять их истинность или ложность, вычисляя соответствующую информацию на основе определенных правил.

Высказывания

Высказыванием может быть любое повествовательное предложение, которое в утвердительной форме выдвигает гипотезу, в отношении которой однозначно можно сказать, истина она или ложна. При этом высказывание может быть записано в виде формального математического выражения или сформулировано на естественном языке. Примеры высказываний:

• Москва — столица России.

• 5>3.

• 2+3=6.

Первое и второе выказывания истинны, третье — ложно. В логических выражениях высказывания, как правило, обозначаются заглавными латинскими буквами: A, B, C…

Высказывания бывают элементарными и составными. Составные высказывания образуются из других высказываний с помощью логических связок: и, или, не, если… , то,тогда и только тогда и др. В булевой алгебре это соответствует применению логических операций в логических выражениях. Высказывания, не являющиеся составными, называются элементарными.

Логические операции

Логические операции булевой алгебры подобны арифметическим операциям элементарной алгебры. Если последние применяются к числам, то первые — к логическим значениям соответствующих высказываний. Составные высказывания можно получать с помощью логических операций так же, как в элементарной алгебре — формулы. И, если известны значения исходных высказываний, значение составного высказывания можно вычислить, прибегая лишь к формальным правилам. Уравнения, составленные в алгебре логики можно формально решать. Все это обеспечивает широкие возможности по применению математического аппарата к суждениям из реальной жизни (там, где не хватает аппарата булевой алгебры, применяются более сложные методы математической логики, в частности, исчисление предикатов первого порядка и др.).

Логические операции можно описывать с помощью таблиц истинности. В такой таблице в колонках стоят операнды операции и сама операция, а в строках — различные значения операндов и результат применения к ним данной операции.

Основные логические операции

Основными логическими операциями являются операции отрицания, логического И и логического ИЛИ. Именно с помощью них наиболее удобно оперировать с логическими выражениями. Производные логические операции могут быть выражены через них.

Отрицание НЕ

Отрицание — операция, применяемая к одному операнду, т.е. унарная операция. Выражение не A записывается как ¬A, A¯¯¯ или !A. Операции отрицания задается следующей таблицей истинности:

A	¬A
0	1
1	0

Соответственно, операции отрицания можно дать следующее истолкование: истинность выражения, построенного с помощью отрицания, противоположна истинности исходного выражения. Если A истинно, ¬A ложно, и наоборот.

В некотором роде операция отрицания подобна операции отрицания в элементарной алгебре. Последняя меняла значение числа на противоположное: положительное на отрицательное и наоборот.

Логическое И

Логическое И (конъюнкция) — операция, применяемая к двум операндам, т.е. бинарная операция. Выражение A и B записывается как A∧B, A⋅B или A&&B. Конъюнкция задается следующей таблицей истинности:

A	B	A∧B
0	0	0
0	1	0
1	0	0
1	1	1

Логическое И, как не сложно понять из названия, образует выражение, которое истинно только тогда, когда истинны оба исходных выражения, входящих в его соста: и первое, ивторое.

Операция конъюнкции подобна умножению. Это легко заметить по таблицы истинности. Конъюнкция дает такой же результат, как если бы мы просто перемножали ее операнды.

Логическое ИЛИ

Логическое ИЛИ (дизъюнкция) — еще одна бинарная операция. Выражение A или B записывается как A∨B, A+B или A||B. Дизъюнкция задается следующей таблицей истинности:

A	B	A∨B
0	0	0
0	1	1
1	0	1
1	1	1

Логическое ИЛИ образует выражение, которое истинно тогда, когда истинно хотя бы одно исходных выражение, входящее в его состав: или первое, или второе.

Операция дизъюнкции подобна сложению. Как и в случае с конъюнкцией, это можно заметить по таблице истинности. Единственным исключением тут является правило 1+1=1, а не 2, как можно было бы ожидать. Но это нормальное явление, учитывая, что пространство логических значений ограничено нулем и единицей.

Производные логические операции

К производным логическим операциям относятся операции исключающего или, импликации, эквивалентности. Они могут применяться при составлении логических выражений, но при дальнейшем анализе выражаются с помощью основных логических операций.

Исключающее ИЛИ

Операция исключающего ИЛИ похожа на обычную дизъюнкцию. Ее обозначают как A⊕B или A^B. Операция задается следующей таблицей истинности:

A	B	A⊕B
0	0	0
0	1	1
1	0	1
1	1	0

Как видно из таблицы, отличие исключающего ИЛИ от дизъюнкции заключается в том, что полученное выражение будет ложным, если истинны оба исходных выражения, а не только одно из них.

Высказывание вида A⊕B в логическом выражении можно заменить на A∧¬B∨B∧¬A.

Операция импликации

Бинарная операция импликации выражается связками если… , то, из … следует, влечет. Операция записывается как A→B или A⇒B и задается следующей таблицей истинности:

A	B	A→B
0	0	1
0	1	1
1	0	0
1	1	1

В импликации A называется посылкой, а B — следствием. Выражение, образованное импликацией, ложно только в том случае, когда посылка истинна, а следствие ложно. При ложной посылке состояние следствия может быть каким угодно.

Высказывание вида A→B в логическом выражении можно заменить на ¬A∨B, при этом оно останется тождественно исходному, то есть будет истинно или ложно ровно в тех же самых случаях, что и оригинальное.

Операция эквивалентности

Данная операция выражается связками тогда и только тогда, необходимо и достаточно, равносильно. Операция имеет следующие обозначения: A≡B, A⇔B, A==B. Таблица истинности выглядит так:

A	B	A≡B
0	0	1
0	1	0
1	0	0
1	1	1

Выражение, образованное эквивалентностью, истинно, если истинность обоих операндов совпадает.

Эквивалентность можно заменить на две импликации, а те, в свою очередь, раскрыть по правилам, указанным выше. Получится, что высказывание вида A≡B можно заменить на A∧B∨¬A∧¬B.

Приоритеты операций

Приоритеты основных логических операций соответствуют приоритетам аналогичных операций в элементарной алгебре. Приоритет исключающего ИЛИ совпадает с приоритетом дизъюнкции. Импликация и эквивалентность обладают равными низшими приоритетами.

Приоритеты логических операций

Отрицание

Конъюнкция

Дизъюнкция, исключающее ИЛИ

Импликация, эквивалентность

Законы булевой алгебры

Как и в элементарной алгебре, логические выражения можно упрощать, чтобы облегчить задачу последующих вычислений или решения уравнений. Эта возможность обусловлена наличием у логических операций и их комбинаций различных свойств, которые позволяют переходить от исходного выражения к тождественному, упрощая его при этом.

В качестве первого шага к упрощению рекомендуется избавиться от всех производных операций в логическом выражении. Поэтому далее будут перечислены только свойства основных логических операций.

Ассоциативность

Ассоциативность конъюнкции и дизъюнкции выражается следующими формулами:

(A∧B)∧C=A∧(B∧C)=A∧B∧C,

(A∨B)∨C=A∨(B∨C)=A∨B∨C.

На практике это означает, что можно опускать те скобки, которые определяют, в каком порядке должна выполняться конъюнкция в выражениях вида A1∧A2∧⋯∧An и дизъюнкция в выражениях вида A1∨A2∨⋯∨An.

Коммутативность

Если операция коммутативна, то результат ее применения не зависит от того, какой из операндов был первым, а какой — вторым. Операнды коммутативных операций можно менять друг с другом местами, получая тождественный результат.

Конъюнкция и дизъюнкция являются коммутативными операциями:

A∧B=B∧A,

A∨B=B∨A.

Дистрибутивность

Свойство дистрибутивности одной операции относительно другой позволяет «раскрывать» скобки аналогично процедуре из элементарной алгебры. Конъюнкция и дизъюнкция дистрибутивны друг относительно друга, что выражается в следующих формулах:

A∧(B∨C)=A∧B∨A∧C,

A∨B∧C=(A∨B)∧(A∨C).

Свойства единицы и нуля

Конъюнкция и дизъюнкция «по-особому» реагируют на единицу или ноль в качестве одного из операндов независимо от значения второго. Эти свойства похожи на знакомые из элементарной алгебры умножение на единицу, умножение на ноль, сложение с нулем:

A∧0=0,A∧1=A,

A∨0=A,A∨1=1.

Идемпотентность

Операция называется идемнотентной, если, применяя ее к двум равным операндам, получается тот же самый операнд. Идемпотентность позволяет «выкидывать» лишние повторные применения операции из формулы. Конъюнкция и дизъюнкция идемпотентны:

A∧A=A,

A∨A=A.

Поглощение

Если к выражению применяется с одним и тем же операндом сначала одна операция, а потом, с тем же самым операндом, поглощающая ее, то значение выражения поглощается, становясь равно операнду. Таким образом поглощающие друг друга пары операций можно «выкидывать» во время упрощения. Конъюнкция и дизъюнкция поглощают друг друга:

A∧B∨B=B,

(A∨B)∧B=B.

Законы де Моргана

Законы де Моргана позволяют применять отрицания к целой скобке, позволяя перейти к так называемым тесным отрицаниям, когда ни одно отрицание не стоит перед скобкой.

¬(A∧B)=¬A∨¬B,

¬(A∨B)=¬A∧¬B.

Дополнение

Отрицание операнда называется его дополнением. Конъюнкция или дизъюнкция операнда со своим дополнением дает однозначные результат независимо от значения операнда:

A∧¬A=0,

A∨¬A=1.

Двойное отрицание

Двойное отрицание компенсирует само себя. Таким образом в форме с тесными отрицаниями у каждой переменной в выражении либо не стоит ни одного отрицания, либо только одно.

¬¬A=A.

Булевы функции

Определение. Переменная x называется булевой, если она способна принимать только два значения 0 и 1. В качестве примера интерпретации такого рода переменных может выступать обычный настенный выключатель света на два положения. Здесь 1 соответствует положению переключателя вверх и 0 — положению вниз. Определение. Функция f(x₁,x₂,…,x_n) называется булевой (или логической, или функцией алгебры логики, или переключательной), если все ее аргументы x[i] являются булевыми, а сама функция также может принимать только два значения 0 и 1. Множество всех булевых функций от переменных x₁,x₂,…,x_n обозначают через P₂.

Способы задания булевых функций

Способы задания булевых функций не отличаются от способов задания обычных функций анализа. К таковым способам задания стандартно относятся: 1) табличный; 2) графический; 3) аналитический.

(1) Табличный способ задания

Пусть w=f(x₁,x₂,…,x_n) — булева функция n аргументов. Область определения данной функции можно рассматривать и как множество упорядоченных наборов (или векторов, или двоичных наборов) D={x₁,x₂,…,x_n | x_i ∈ {0,1}, i=1,2,…,n}, на каждом из которых функция принимает одно из двух значений: w ∈ {0,1}. Количество таких наборов (x₁,x₂,…,x_n), согласно правилу прямого произведения, равно |D|=

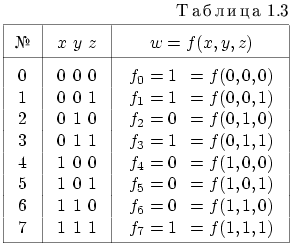
В качестве примера рассмотрим табличное представление булевой функции трех аргументов w=f(x,y,z), где w,x,y,z  ∈ {0,1}. Область определения функции — это множество двоичных наборов D={(x,y,z), |  x,y,z ∈ {0,1}}. Их число есть |D|=2^3=8, а количество таких функций равно 2^|D|=2^2^3=256. Значения функции f(x,y,z) удобно представить в виде табл. 1.3, где перечислены всевозможные наборы из нулей и единиц длины 3 и для каждогонабора указано значение функции fⁱ ∈ {0,1} на этом наборе.

В таблицах, аналогичных табл. 1.3 обычно употребляется расположение наборов, соответствующих порядку естественного роста двоичных чисел 0,1,…2^n-1, в примере n=3. Определение. Таблицы значений булевых функций, подобные табл. 1.3, называются таблицами истинности булевых функций. Название таблиц происходит от интерпретации значений 1 — истина (TRUE), 0 — ложь (FALSE).

(2) Графический способ задания

Рассмотрим графическое представление булевой функции трех аргументов w=f(x,y,z), заданной таблично (табл. 1.3). Заметим, что множество наборов области определения функции D={(x,y,z) , | x,y,z ∈ {0,1}} является множеством координат точек вершин единичного трехмерного куба (рис. 1.2). 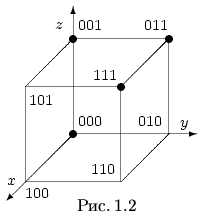Очевидный способ графического представления булевой функции — это отметить каким-то образом вершины куба, в которых функция принимает значение 1. Именно так на рис. 1.2 и сделано. В соответствии с таблицей значений (табл. 1.3) отмечены вершины, в которых булева функция равна 1.

Замечание. Очевидно, что область определения булевой функции n аргументов w=f(x₁,x₂,…,x_n) составляется из наборов координат точек вершин единичного n-мерного куба.

(3) Аналитический способ задания

Приведем таблицы истинности, обозначения и названия булевых функций одного и двух аргументов. В табл. 1.4 представлены все (их 2^2^1=4) функции одного аргумента, в табл. 1.5 — все функции двух аргументов (их 2^2^2=16).

Таблица 1.4

x	0 1	Обозначение	Название
0	0 0	0	Нуль, const 0
1	0 1	x	Повторение x
2	1 0	¬x, x	Отрицание x, не x
3	1 1	1	Единица, const 1

Функции 0 и 1 называются соответственно тождественным нулем и тождественной единицей. Иногда эти функции 0 и 1 рассматривают как функции, зависящие от пустого множества переменных.

Таблица 1.5

x у	0 0 1 1 0 1 0 1	Обозначение	Название
0	0 0 0 0	0	Нуль, const 0
1	0 0 0 1	x•y,x∧y,x&y	Конъюнкция
2	0 0 1 0	yx,x•y	Запрет по x
3	0 0 1 1	x	Повторение x
4	0 1 0 0	x, x•y	Запрет по y
5	0 1 0 1	y	Повторение y
6	0 1 1 0	x⊕y	Сумма по модулю 2
7	0 1 1 1	x∨y	Дизъюнкция
8	1 0 0 0	x↓y	Стрелка Пирса
9	1 0 0 1	x~y	Эквивалентность
10	1 0 1 0	¬y, y	Отрицание y
11	1 0 1 1	y→x, y⇒x, y⊃x	Импликация от y к x
12	1 1 0 0	¬x, x	Отрицание x
13	1 1 0 1	x→y, x⇒y, x⊃y	Импликация от x к y
14	1 1 1 0	x|y	Штрих Шеффера
15	1 1 1 1	1	Единица, const 1

Функции одного и двух аргументов, представленные в таблицах 1.4 и 1.5, называются элементарными.

Символы ¬, |, ↓, ∧, , ∨, →, ⊕, ~, участвующие в обозначениях элементарных функций, называются логическими связками (операциями) или функциональными символами.