KGiG_exam_shpora / 4. Связь преобразований объектов с преобразованием координат / 1

Связь преобразований объектов c преобразованиями координат

Когда пользователь графической системы видит на экране перемещающийся объект, то, как вы считаете, что на самом деле происходит — перемещаются объекты или система координат в обратном направлении? Например, если в кино вы видите объекты, вращающиеся на экране по часовой стрелке, то может в действительности это камера поворачивается против часовой стрелки?

Преобразование объектов и преобразование систем координат тесно связаны между собой. Движение объектов можно рассматривать как движение в обратном направлении соответствующей системы координат.

Такая относительность для объектов отображения и систем координат дает разработчикам компьютерных систем дополнительные возможности для мо-делирования и визуализации пространственных объектов. С каждым объек­том можно связывать как собственную локальную систему координат, так и единую для нескольких объектов. Это можно использовать, например, для моделирования подвижных объектов.

Обычно, того же самого эффекта можно добиться, если использовать различные подходы. Однако в одних случаях удобнее использовать преобразование координат, а в других — преобразование объектов. Не последнюю роль иг­рает сложность обоснования какого-то способа, его понятность.

Рассмотрим пример комбинированного подхода. Пусть нам нужно получить функцию расчета координат (X, Y) для поворота вокруг центра с координата­ми (Xo, Yo) (рис. 2.13).

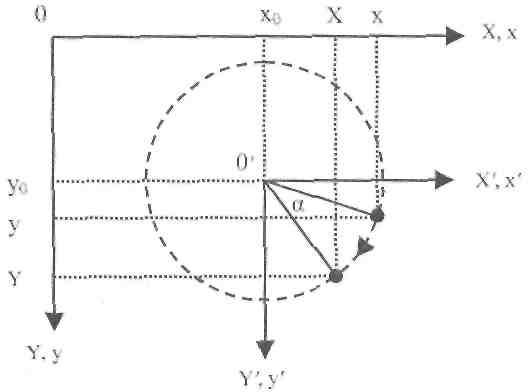
Рис. 2.13. Вращение вокруг произвольного центра

Выше мы рассмотрели поворот относительно центра координат (0, 0). Для решения нашей задачи введем новую систему координат (x’O’y’) с центром в точке (х₀, у₀):

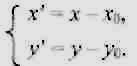
Для такой системы поворот точек происходит вокруг ее центра:

Преобразуем координаты (X’,Y’) в (X,Y) сдвигом системы координат в

точку (0,0).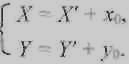

Если объединить формулы преобразований, то получим результат:

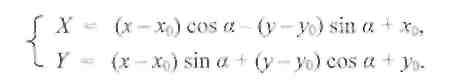
Решение этой задачи можно было бы осуществить и в матричной форме:

Рассмотрим второй пример. Нашей задачей будет вывод формул параметри­ческого описания поверхности тора. Изобразим тор следующим образом (рис. 2.14).

Для произвольной точки Р, лежащей на поверхности тора, требуется выра­зить координаты (х, у, z) через константы, описывающие размеры фигуры, а также через некоторые параметры. Для поверхности в трехмерном простран­стве необходимо использовать два параметра. В качестве таковых выберем угловые величины: φ(широта) и ω (долгота).

Непосредственное определение координат точки Р представляется сложным, поэтому искомые координаты будем искать несколькими шагами преобразо­ваний. Рассмотрим окружность, лежащую в плоскости zOy, центр этой ок­ружности совпадает с центром координат. Координаты точки Р" с широтой <р составляют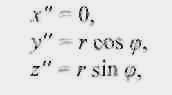

где r— малый радиус тора.

Теперь перенесем окружность на расстояние R (большой радиус тора) по оси у в той же плоскости zOy. Получим точку P’. Ее координаты:

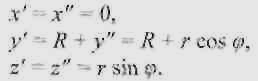
Окружность, которой принадлежит точка Р', является геометрическим ме­стом точек тора с нулевой долготой (о. Если точку Р' повернуть на угол to, то получим искомую точку Р поверхности тора с координатами

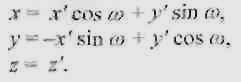
Подставляя значения x’,y’,z’ получим искомые формулы:

Эту задачу можно было бы решить, используя преобразование координат. Подобный случай мы рассмотрим ниже (пример studex8 в разделе програм­мирования). Однако, как представляется, более ясным здесь выглядит ис­пользование операций перемещения точки (из положения P’’ в P’, а за­тем в Р).