FM_MMMFP (1) / Курсяк_мат_методы (исправьте даты на рисунках pde)

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Воронежский государственный технический университет

Физико-технический факультет

Кафедра высшей математики и физико-математического моделирования

КУРСОВАЯ РАБОТА

по дисциплине «Математические методы моделирования физических процессов»

Тема: Моделирование задач теплопроводности и диффузии методом конечных элементов.

Выполнил студент ТФ - 081 Д.С. Дикарев

группа подпись инициалы, фамилия

Руководитель И.Л. Батаронов

подпись инициалы, фамилия

Нормоконтроль И.Л. Батаронов

подпись инициалы, фамилия

Защищена________________ Оценка_____________________

2010г.

Воронежский государственный технический университет Кафедра высшей математики и физико-математического моделирования

ЗАДАНИЕ

на курсовую работу

по дисциплине «Математические методы моделирования физических процессов»

Специальность 140400: «Техническая физика»

Тема работы: Моделирование задач теплопроводности и диффузии методом конечных элементов.

Список вопросов подлежащих разработке:

1. В шаре радиуса R действует источник тепла с постоянной плотностью Q, а поверхность охлаждается по закону Ньютона. Начальная температура круга равна температуре среды. Найти распределение температур круга и минимальную температуру нагрева.

2. Найти установившееся распределение концентраций вокруг сферы, если плотность потока диффузанта через неё описывается выражением 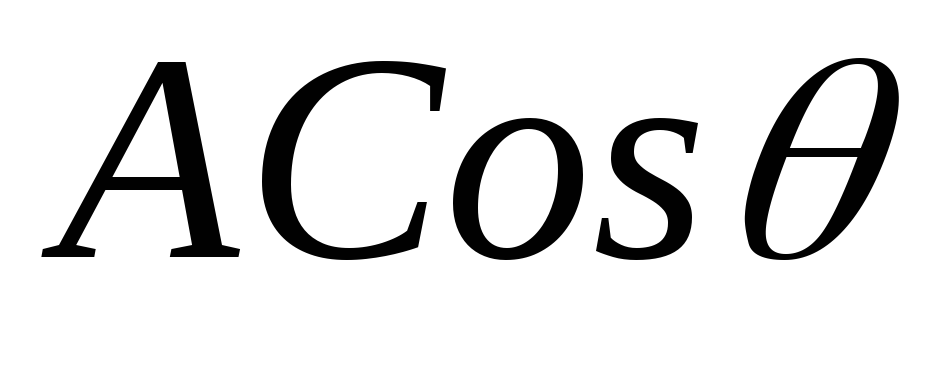. Нарисовать следы концентрационных поверхностей.

Дата выдачи задания_______________________

Дата сдачи курсовой работы_________________

Дата защиты______________________________

Руководитель работы: И.Л. Батаронов

^{подпись инициалы, фамилия}

Задание принял студент Д. С. Дикарев

^{подпись инициалы, фамилия}

Содержание

		Стр
	Введение………………………………………………………………	4
	Решение задачи № 1………………………………………………….	5
	Решение задачи № 2………………………………………………….	8
	Заключение……………………………………………………………	11
	Список использованной литературы………………………………..	12

Введение

В процессе диффузии искомой функцией является концентрация диффундирующего вещества, которую обычно обозначают через c = c(x, y, z, t). Функция c = c(x, y, z, t) удовлетворяет уравнению

.

Положительный коэффициент D называют коэффициентом диффузии. Начальное условие

задаёт начальную концентрацию. В качестве краевых условий рассматриваются главным образом условия

,

где Г – граница области, в которой происходит диффузия. Первое условие означает, что Г является непроницаемой для диффундирующего вещества стенкой, а второе условие задаёт концентрацию на границе Г [3].

Уравнения параболического типа получается при исследовании таких физических явлений, как теплопроводность, диффузия, распространение электромагнитных полей в проводящих средах, движение вязкой жидкости.

К уравнениям эллиптического типа приводит изучение стационарных (не меняющихся во времени) процессов различной физической природы. Сюда относятся стационарные электрические и магнитные поля (электростатика, магнитостатика, поля постоянного электрического тока), потенциальное движение несжимаемой жидкости, стационарные тепловые поля и др. Простейшим уравнением эллиптического типа является уравнение Лапласа . В отличие от уравнений параболического и гиперболического типов краевые задачи для эллиптического уравнения характеризуются отсутствием начальных условий. В зависимости от типа краевых условий для уравнения Лапласа различают: первую краевую задачу – задачу Дирихле – при , вторую краевую задачу – задачу Неймана – при , третью краевую задачу, если , где – некоторые функции, заданные на границе Σ области, в которой ищется решение уравнения Лапласа.

Поставить краевую задачу, соответствующую данной физической задаче, – это значит выбрать функцию, характеризующую физический процесс, а затем:

1. вывести дифференциальное уравнение для этой функции;

2. установить для неё граничные условия;

сформулировать начальные условия [2].

Решение задачи № 1.

В шаре радиуса R действует источник тепла с постоянной плотностью Q, а поверхность охлаждается по закону Ньютона. Начальная температура шара равна температуре среды. Найти распределение температур круга и минимальную температуру нагрева.

Для решения задачи будем использовать специальное приложение FlexPDE 6.

Предположим, что температура среды равна нулю, коэффициент теплопроводности равен K = 0.05 Вт/(м*К), объемная плотность мощности источников тепла Q = 5 Вт/м³, а коэффициент конвективного теплообмена расчетной области с окружающей средой равен h = 15 Вт/(м²*К)

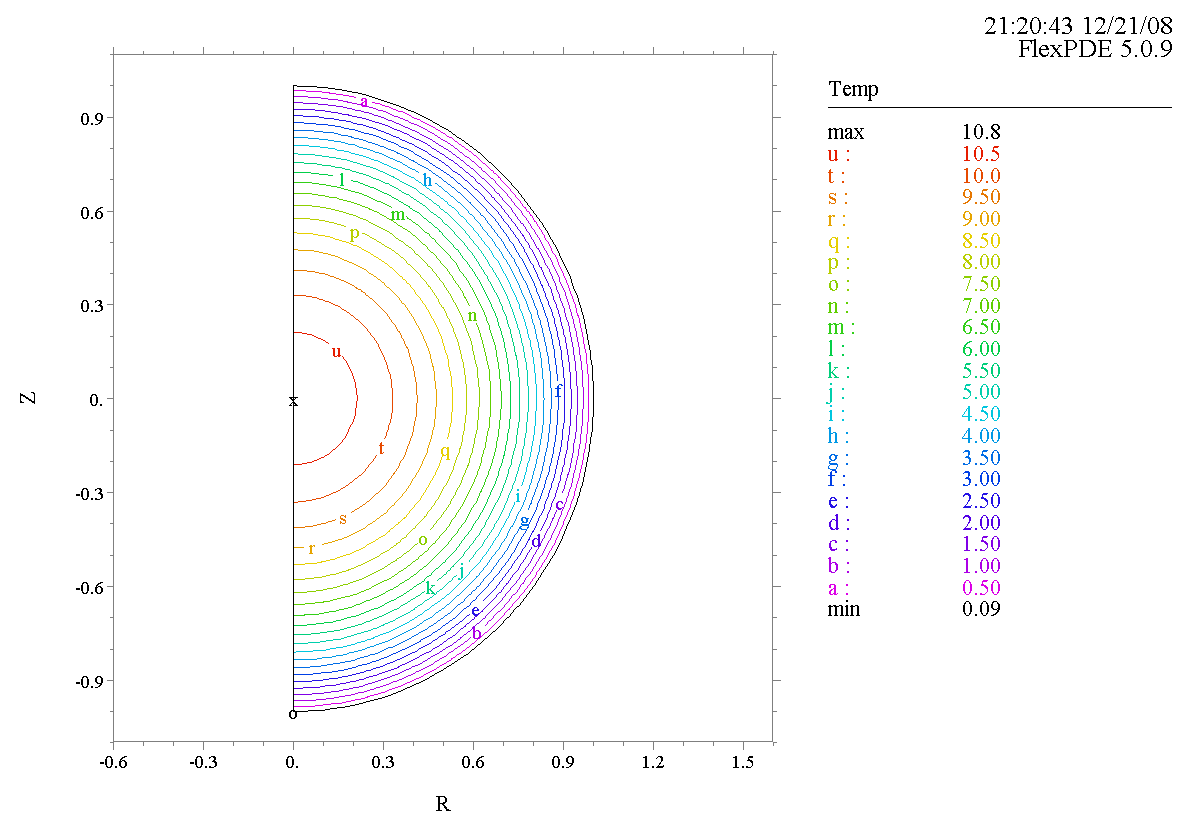
Рисунок1. Распределение температуры

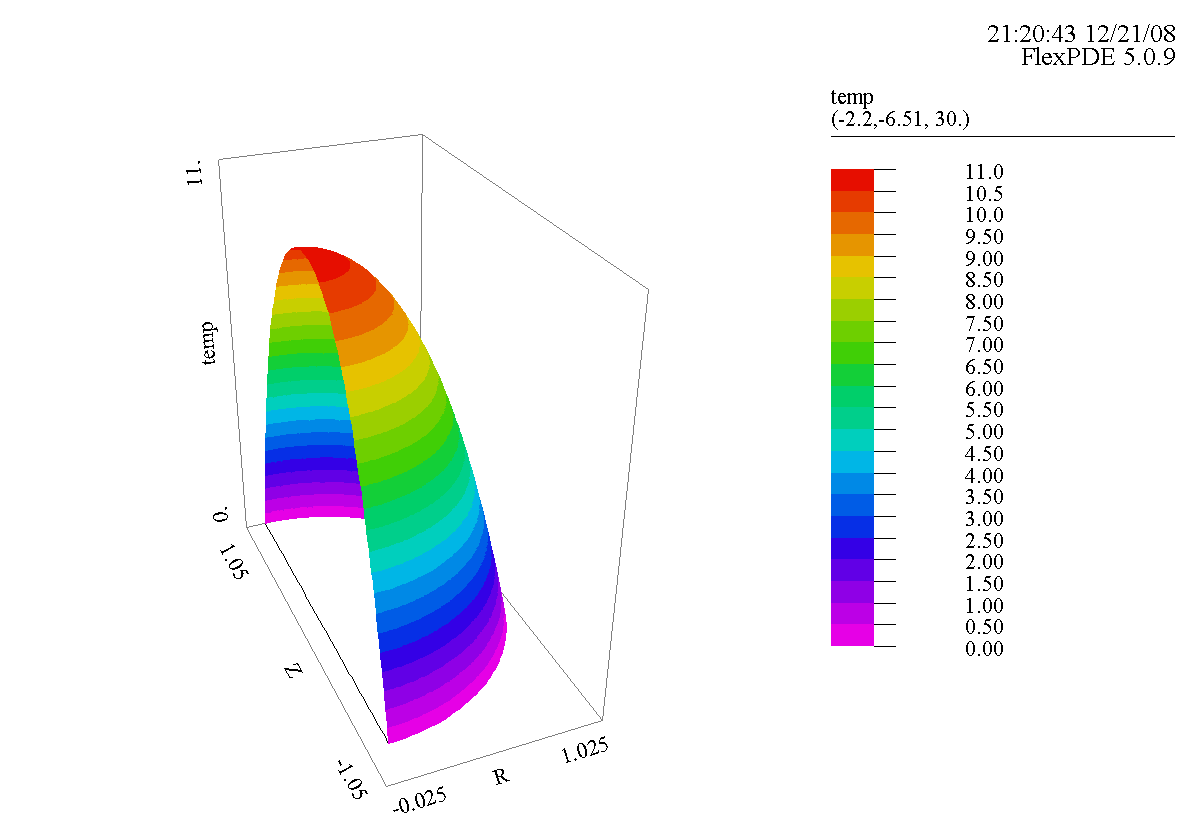
Рисунок 2. Поверхность распределения температуры

Рисунок 3. Направления потока температуры

По картине распределения мы можем найти минимальную температуру нагрева круга. T_min = 1 K.

Решение задачи № 2.

Найти установившееся распределение концентраций вокруг сферы, если плотность потока диффузанта через неё описывается выражением . Нарисовать следы концентрационных поверхностей.

В нашей задаче объемная плотность источника диффузанта равна нулю, т.к. объёмных источников нет. Поэтому уравнение будет иметь вид: div(grad(N)) = 0.

Для задания условия на границе сферы необходимо выразить через координаты R и Z. Получим, что

Для решения задачи будем использовать специальное приложение FlexPDE 6:

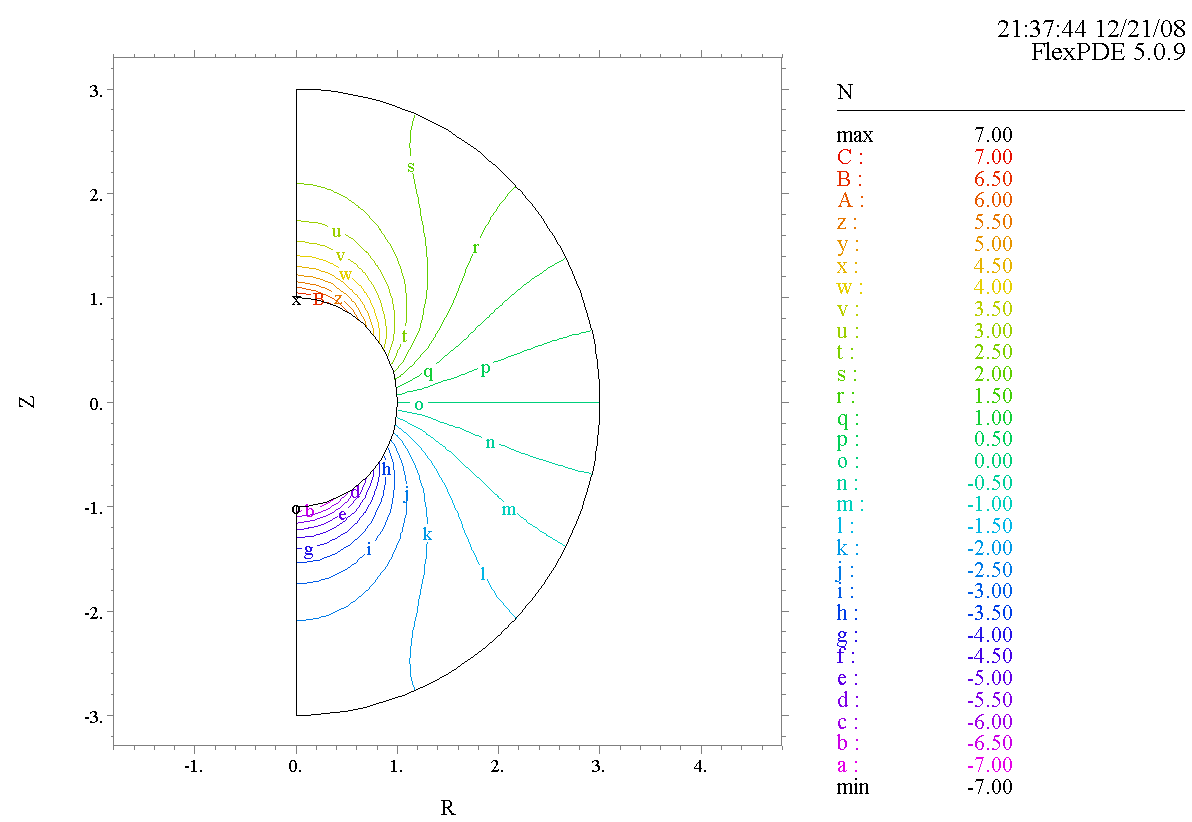
Рисунок 4. Распределение концентрации

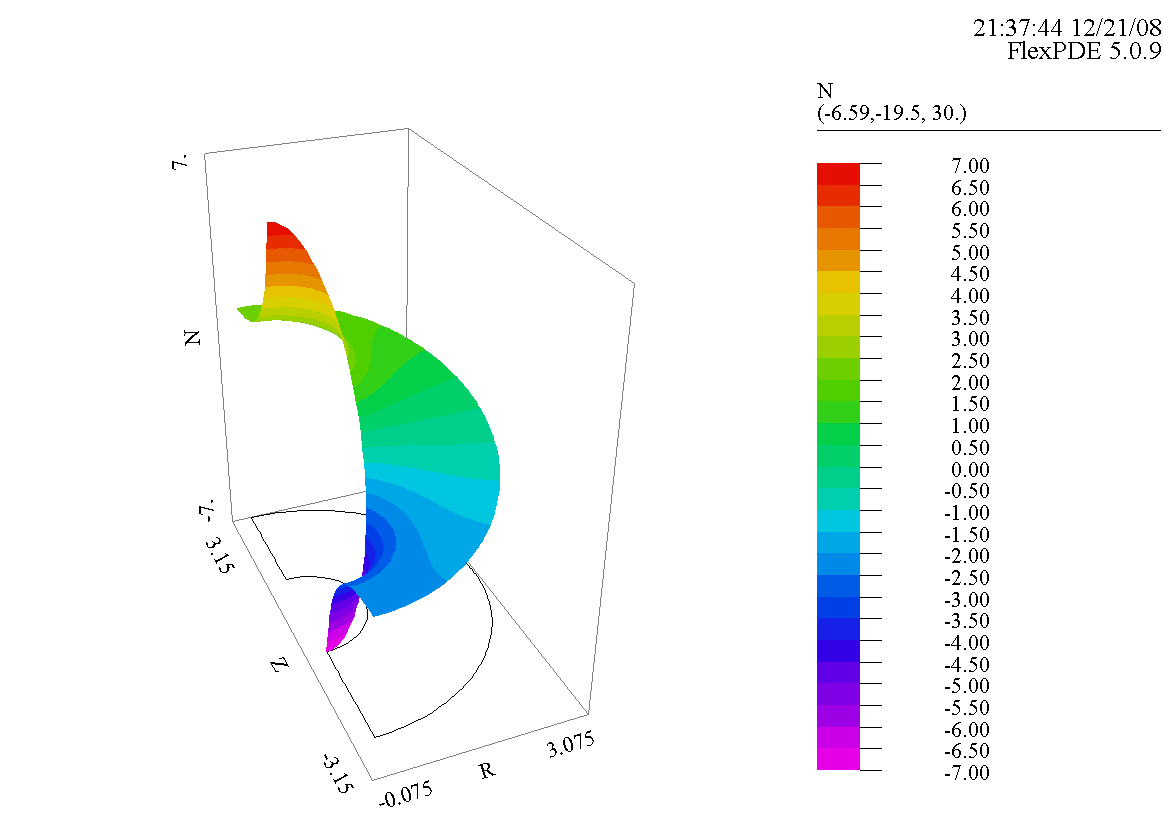
Рисунок 5. Поверхность распределения концентрации

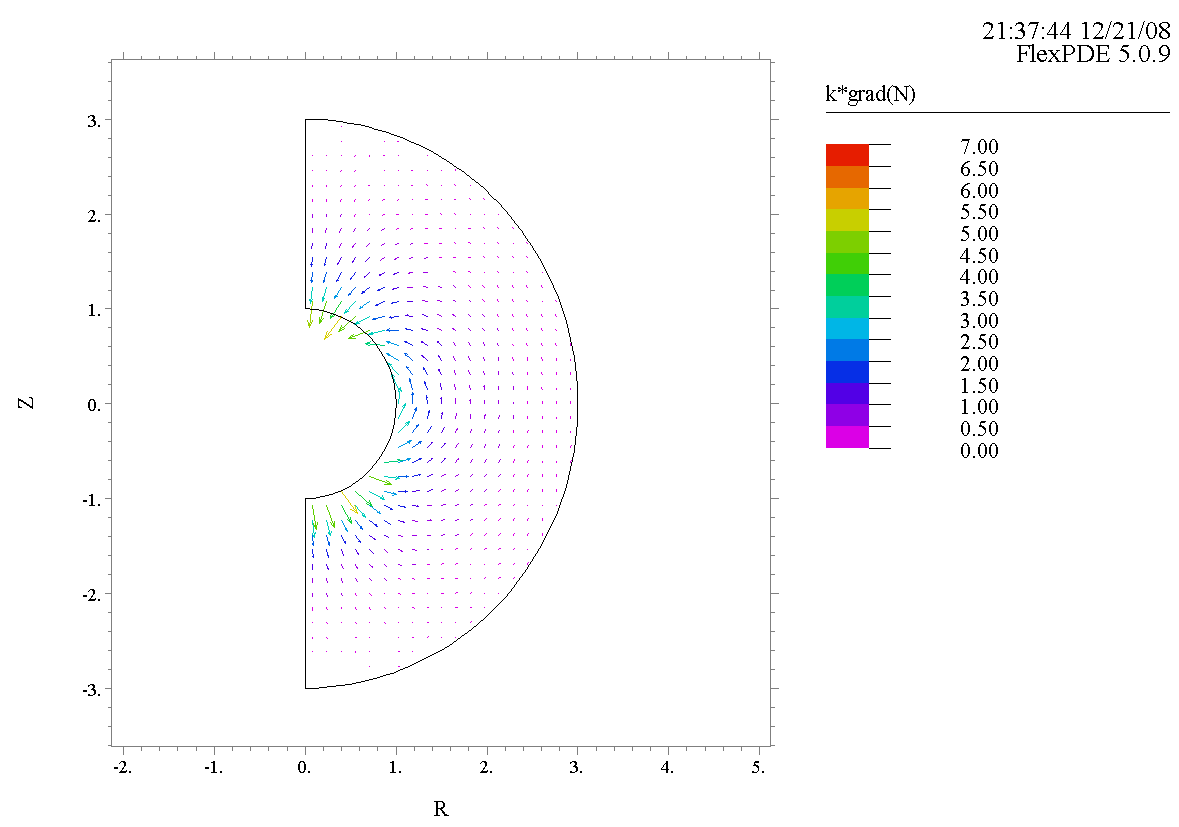
Рисунок 6. Направления потока концентрации

Заключение.

В данной работе мы моделировали уравнения диффузии и теплопроводности с помощью приложения FlexPDE. В задаче теплопроводности решалось уравнение параболического типа, и в итоге были получены графики распределения температур круга, в котором действует объемный источник тепла, а поверхность охлаждается по закону Ньютона. По картине стационарного распределения была определена минимальная температура нагрева круга.

Во второй задаче решалось элептическое уравнение диффузии с поверхности сферы. В итоге была получена картина установившегося распределения диффузанта и следы концентрационных поверхностей.

Список используемой литературы

1. Будак Б. М., Самарский А. А., Тихонов А. Н. Сборник задач по математической физике. – 4-е изд., испр. – М.: Наука, 2004. – 688 с.

2. Араманович И. Г., Левин В. И. Уравнения математической физики. – 2-е изд. – М.: Наука, 1969. – 288 с.

12