§ 5. Корреляционный анализ экспериментальных данных § 5. Корреляционный анализ экспериментальных данных

5.1. Построение корреляционной матрицы

Математическая теория корреляции изучает на­ли­чие за­ви­си­мос­ти между исследуемыми ве­ли­чи­на­ми. Ос­нов­ным применением кор­ре­ля­ци­он­ных методов об­ра­ботки экс­пе­ри­ментальных дан­ных являются про­гноз­ные задачи, связанные с оп­ре­­де­ле­ни­ем пределов, в ко­то­­рых наперед с за­дан­ной надежностью будут со­дер­жать­ся ин­те­ре­су­ю­щие исследователя величины. Так, на­при­мер, ис­­сле­дователя может ин­тересовать вли­я­ние на то или иное явление некоторых факторов, связь не­ко­то­рых признаков, выделение связ­ных групп ис­следуемых объек­тов и пр.

Довольно часто случайная величина, по­лу­ча­е­мая из экс­перимента, пред­став­лена таблицей по­ряд­ка m´n, где m - количество наблюдений; n - количество фи­к­­си­ру­е­мых переменных. Для того чтобы вы­яс­нить, зависимы или нет эти пе­ре­мен­ные, вы­чис­ля­ют меру взаимной из­мен­чивости пары пе­ре­мен­ных. Эта ме­ра называется ко­ва­риацией и является ха­рактеристикой совместного из­ме­­не­ния двух пе­ре­менных по отношению к их общему сред­нему зна­чению. Ины­ми словами, ковариация яв­ля­ет­ся ме­­рой разброса значений от­но­сительно общего сред­­­него.

Для вычисления коэффициента ковариации вве­­дем ве­личину, ана­ло­гич­ную сумме квадратов, назовем ее цент­рированной суммой сме­­­шан­ных произведений (SР_jk) и будем оп­ре­делять по формуле

,

где x _ij - i-е значение j-й переменной; x_ik - i-е зна­че­ние k-й переменной; - средние значения j-й и k-й пе­ре­мен­ных. Пе­ре­пи­шем SР_jk в форме, удобной для вы­чис­ле­ний:

_.

Если выбрать j = k, то последняя формула пре­об­ра­зу­ется к виду

_.

Из этой формулы видно, что SS_j - дис­пер­сия ве­ли­чин x _ij при условии, что SS_j будет раз­делена на (N - 1) или N для цент­ри­ро­ван­ной величины.

Предположим, что в результате некоторого экс­пе­ри­мен­та бы­ли исследованы три переменные А, B и С. Подсчитав центри­ро­ван­ные про­из­ве­де­ния перемен­ных А, B и С, получим табл. 7.7.

Таблица 7.7

	А	В	С
А	SSa	SРab	SРac
В	SРba	SSb	SРbc
С	SРca	SРcb	SSc

Легко заметить, что эта таблица симметрична от­носительно диагональных эле­ментов, так как SР_ab = =SР_ba; SР_bc = SР_cb ; SР_ac = SР_ca.

Если теперь разделить каждый элемент таб­ли­цы на (N - 1), то получим фун­кцию ковариации

которая, как уже отмечалось, характеризует сов­местное из­менение двух пе­ременных по от­но­ше­нию к их об­ще­му среднему значению. Заметим по­­пут­но, что ин­тер­пре­та­ция значений оценок ко­ва­риаций должна про­во­дить­ся та­ким же образом, как и для дисперсий (см. § 1), но при этом сле­дует помнить, что рас­смат­риваемые зна­че­ния зависят от единиц из­мерения, так как являются раз­мер­ными.

Для оценки степени взаимной связи между пе­ре­мен­ны­­ми, которая не зависит от еди­ниц измерения, на прак­тике поль­зу­ют­ся коэффициентом взаимной кор­­ре­ля­­ции Â_jk, который вычисляется как от­но­ше­ние ко­ва­ри­а­ции двух пере­мен­ных к про­из­ве­де­нию их стан­дар­т­ных от­­кло­не­ний, т.е. . Как видно из фор­­­му­лы, Â_jk - это без­раз­мерная величина. При этом ко­вариация мо­­жет рав­нять­ся произведению стан­дар­т­ных от­кло­не­ний рас­смат­ри­ва­е­мых пе­ременных, но не мо­­жет быть боль­ше его. Поэтому Â_jk изменяется на ин­тер­­­­­­вале [-1, 1]. Причем, если Â_jk = 1, то это ука­зы­ва­ет на пря­мую линейную связь меж­ду пе­ре­мен­­ны­ми, а если Â_jk = -1, то это указывает, что од­­на пе­ре­мен­ная является пол­ной про­ти­во­полож­нос­тью дру­гой. Меж­ду этими дву­­мя крайними слу­ча­я­ми имеется спектр зна­чений, ко­то­рый показывает силь­ные свя­зи меж­ду пе­ре­мен­ными, а если Â_jk = 0, то на полное от­сут­ст­вие ли­нейной свя­зи.

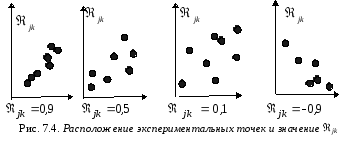
На рис.7.4 показанo несколько типов очевидной связи между пе­ре­мен­ны­ми.

Коэффициент ли­ней­ной кор­реляции удобно вы­чис­ляеть по следующей формуле:

_.

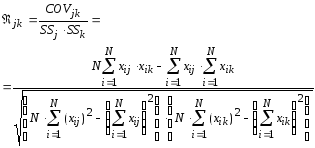Заметим, что коэффициент корреляции есть ме­ра ли­ней­ной зависимости меж­ду двумя пе­ре­мен­ны­ми. Но на прак­тике часто оказывается, что переменные связаны между собой нелинейными зависимостями, тогда ко­эф­фи­ци­ентом линейной кор­ре­ляции пользоваться нель­зя. В этом слу­чае вычисляют ко­эф­фи­ци­ент нелинейной кор­­­реляции.

При оценке Â_jk возникает проблема опре­де­ле­ния пре­дельно до­пус­ти­мо­го отклонения от нуля вы­бо­роч­но­го ко­эф­фициента корреляции. Это от­кло­­не­ние мож­но рас­счи­тать из распределения Стью­дента [Корн Г., Корн Т., 1978; Са­­марский, Гу­лин, 1989; Численные..., 1976], если по­ло­жить N - 2 - число сте­пе­ней свободы и сфор­мулировать ну­ле­­вую гипотезу H₀:R* = 0, где R*- ко­­эф­фи­циент связ­ности (ну­левая гипотеза говорит, что связи меж­ду ве­ли­чинами нет):

,

где a - уровень значимости; f = N - 2 - количество на­блю­дений; t_a,f - выбирается из таб­л. 7.8, в которой при­ве­де­ны не­которые критические значения для выборочного ко­эф­фи­циента корреляции согласно критерию Фишера [Са­мар­с­кий, Гулин, 1989].

Таблица 7.8

N	t0.05	t0.10	N	t0.05	t0.10	N	t0.05	t0.10
1	0.997	1.00	16	0.468	0.590	110	0.186	0.242
2	0.950	0.980	17	0.456	0.575	120	0.178	0.232
3	0.878	0.959	18	0.444	0.561	130	0.171	0.223
4	0.811	0.917	19	0.433	0.549	140	0.165	0.215
5	0.754	0.875	20	0.423	0.537	150	0.160	0.210
6	0.707	0.834	21	0.381	0.487	200	0.139	0.182
7	0.666	0.798	30	0.349	0.449	300	0.113	0.148
8	0.632	0.765	35	0.325	0.418	400	0.098	0.129
9	0.603	0.735	40	0.304	0.393	500	0.088	0.115
10	0.576	0.708	50	0.273	0.354	600	0.080	0.105
11	0.553	0.684	60	0.250	0.325	700	0.074	0.097
12	0.552	0.661	70	0.232	0.302	800	0.069	0.091
13	0.514	0.614	80	0.217	0.283	900	0.065	0.086
14	0.497	0.624	90	0.205	0.267	1000	0.062	0.081
15	0.482	0.606	100	0.195	0.254

Если теперь |Â_jk| < t_a, то гипотеза принимается, т.е. меж­ду величинами нет значимой связи. Ес­ли |Â_jk| > t_a, то гипотеза от­кло­ня­ет­ся, а кор­ре­ли­ру­е­мые признаки считают ли­ней­но связанными.