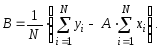§ 1. Эмпирические линейные зависимости
Глава 7. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА
ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ (введение в регрессионный и корреляционный анализ)
§1. ЭМПИРИЧЕСКИЕ ЛИНЕЙНЫЕ ЗАВИСИМОСТИ
1.1. методы построения линейных зависимостей и уточнение их параметров
Анализ экономических, технических,физических процессов приводит к необходимости выявления существенных факторов, влияющих на исследуемый процесс, а также выбора формы связи между этими факторами и оценки параметров полученных уравнений связи.
Будем считать, что некоторое явление характеризуется двумя величинами {Х} и {Y}, связанными между собой некоторой неизвестной экспериментатору функциональной зависимостью. Любую из этих величин с одинаковой степенью можно считать независимой, тогда как другая будет считаться зависимой. Пусть, например, независимой положим переменную {X}. Тогда говорят, что переменнаяY связана с {X} некоторой зависимостью, которую без ограничения общности можно представить какY = F(Х), гдеF- некоторый неизвестный оператор, определяющий правило перехода от множестваХко множествуY. Для простоты можно считать преобразование взаимно однозначным, хотя на практике это выполняется далеко не всегда.
Теперь математически задача сводится к построению явного вида оператора F и затем его уточнению. Методов решения указанной задачи существует достаточно много. Рассмотрим методылинейного регрессионного анализа.

Метод среднихдает лучшие результаты по сравнению с методом выбранных точек. Если предположим, что зависимость построена, тогдаyi = aхiдаст приближенные значенияyi. Определим параметр aиз условия минимума средней ошибки
![]() .
.
Перепишем последнее выражение в виде
![]() ,
,
преобразуя которое получим выражение для
![]() .
.
Метод наименьших квадратов дает еще более точныерезультаты по сравнению с рассмотренными. В этом методе параметраопределяется из условия минимальной суммы квадратов отклонений табличных значенийуi от полученныхуi* :
![]() .
.
Условие минимума F, как известно,
дает равенство нулю ее
первой производной,
т.е.
![]() .
ПродифференцировавFпоа, получим
.
ПродифференцировавFпоа, получим
![]() ,
откуда находим
,
откуда находим
![]() .
.
Каждый из приведенных методов является болееточным по сравнению с предыдущим, поэтому рекомендуется сначала воспользоваться методом выбранных точек, а затем - одним из двух оставшихся.
Пусть теперь В № 0. Посмотрим, как изменятся методы. Общий вид зависимости теперьYi = АХi + В.
Для уточнения параметров АиВвоспользуемся рассмотренными методами.
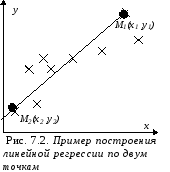
метод выбранных точек. Выберем на построенном графике две произвольные точкиМ1(х1,у1) иМ2(х2,у2) (рис. 7.2). Из аналитической геометрии известно, что уравнение прямой будет
![]() ,
,
откуда получаем
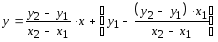 .
.
Тогда выражения для параметровАиВможно определить как
![]() .
.
Метод средних. Согласно емуАиВищем такими, чтобы алгебраическая сумма всех уклонений от вычисленных значений была бы равна нулю:
![]() .
.
Для определенияАиВ разобьем все данные на две группы так, чтобы сумма алгебраических уклонений каждой группы от среднего была бы равна нулю. Иными словами среднее для одной группы точек было быравным (или не очень сильно отличалось) среднему другой группы точек. Тогда для каждой группы запишем
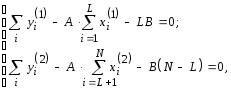
где L- число элементов в I группе. Из последней системы найдемА и В :
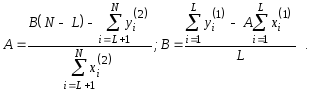
Выполнив над последними выражениями элементарные алгебраические преобразования, получим окончательно выражения для коэффициентовАиВ:
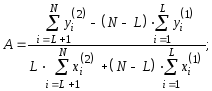
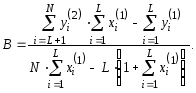
Метод наименьших квадратов. Согласно ему ищем минимум функции
![]() .
.
Используя условие экстремума функции F, находим
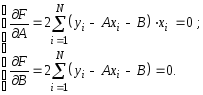
От последней системы можно перейти к более простой, выполнив элементарные алгебраические преобразования

Решая последнюю систему относительно АиВ, получаем