§ 1. Основные понятия математической статистики
Глава 6. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ (введение в математическую статистику)
§ 1. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Численные методы, как правило, применяют при математическом моделировании процессов, которые имеют место в самых различных областях знаний: физике, экономике, психологии, геологии, медицине и др. Результаты моделирования при этом сравнивают с экспериментальными данными. По степени их согласованности делают заключение о соответствии или несоответствии выбранной математической модели моделируемому процессу. Чтобы обоснованно делать это заключение, а также уметь из экспериментальных данных извлечь необходимую информацию об объекте исследования, экспериментатор должен владеть методами статистической, регрессионной и корреляционной обработки экспериментальных данных.
Статистические методы направлены в основном на установление закономерностей, которым подчиняются массовые случайные явления - некоторые реальные процессы, подвергающиеся случайным воздействиям. Случайный эксперимент или опыт есть процесс, при котором возможны различные исходы, так что заранее нельзя предсказать, каков будет результат. Однако опыт характеризуется тем, что его можно повторить много раз, меняя или нет условия эксперимента. Кроме того, полученные результаты можно обрабатывать различными способами, группируя их так, как это необходимо для лучшего выявления закономерностей. Таким образом, в задачи математической статистики входят:
1) указание способов сбора и группировки сведений, полученных в результате наблюдений или как результат некоторых экспериментов (измерений);
2) разработка методов анализа полученных экспериментальных данных в зависимости от целей исследований.
Напомним коротко некоторые понятия и определения.
Случайной величиной (элементом) назовем такую величину, которая принимает в результате эксперимента одно и только одно возможное значение из некоторой их совокупности и неизвестно заранее, какое именно.
По результату отдельного эксперимента нельзя заранее указать точное значение случайной величины, но по совокупности, полученной в эксперименте, можно изучать некоторые закономерности ее поведения, т.е определять вероятностные характеристики случайной величины.
Под совокупностью будем понимать множество (конечное или бесконечное) элементов, рассматриваемых как однотипные измерения, полученные на объектах заданного типа.
Под выборкой будем понимать подмножество элементов, выбранных из некоторой совокупности.
Подмножество элементов, из которого производится выборка, будем называть генеральной совокупностью, а количество объектов (в генеральной совокупности или в выборке) - объемом совокупности.
Если из выборки заранее исключают элементы с заданными свойствами, то такую выборку будем называть смещенной. Если отобранный из выборки объект возвращается в генеральную совокупность перед выбором очередного объекта, то такую выборку будем называть повторной, если же объект не возвращается, то бесповторной. Если по данной выборке можно уверенно судит об изучаемом признаке генеральной совокупности, то такую выборку будем называть репрезентативной (представительной).
Параметрами будем называть статистические характеристики, определенные для совокупности, а если эти характеристики относятся к выборке, то статистиками. Заметим попутно, что статистики можно использовать для оценки параметров исходных совокупностей, для проверки гипотез и пр. Все эти признаки можно условно разделить на качественные и количественные.
Случайные величины можно условно подразделить на дискретные и непрерывные. В то время как первые принимают вполне определенные значения х1, х2, ..., хк с вероятностями соответственно р1, р2, ..., рк, то вторые распределены с некоторой плотностью по некоторому отрезку прямой ОХ.
§ 2. МАТЕМАТИЧЕСКИЕ ОЦЕНКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ. ПРОВЕРКА ГИПОТЕЗЫ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
Пусть теперь из генеральной совокупности извлечена выборка, причем х1 наблюдалось n1 раз, х2 - n2 раза, ..., хк - nк раз, тогда наблюдаемые значения назовем вариантами, последовательность вариант, записанных в возрастающем порядке, вариационным рядом, количество наблюдений nк назовем частотами, а отношение частот к общему объему выборки ni/N = Wi - относительными частотами.
Если, например, задано распределение частот выборки объема N = 20:
-
хi
2
6
12
ni
3
10
7 ,
Наиболее используемая характеристика совокупности - это ее среднее значение
,
(6.1)
,
(6.2)
где pi - вероятность
появления i-го случайного события.
Отметим, что при достаточно большом
числе наблюдений N величина
,
вычисленная по формуле (6.1) или (6.2),
стремится к истинному
математическому
ожиданию z, которое
также характеризуется
как случайная величина:
,
здесь рi - вероятность
появления случайного
события xi
. Чем больше N, тем с большей
надежностью можно утверждать,
что
.
Очевидно, что ошибка равенства
носит вероятностный
характер и описывается
некоторым интервалом
.
Этот интервал зависит от закона распределения случайной величины, который также является ее универсальной характеристикой.
Функция распределения определяет для каждого значения хi на числовой оси вероятность того, что случайная величина X примет значение, меньшее чем хi, т.е. F(хi) = =Р(X < хi ). Функция распределения F(хi) существует для непрерывных и дискретных величин. Она обладает следующими свойствами:
1) F(хi) - непрерывна;
2)
3)
4)Р(х1<Х<х2)
= F(х1)- F(х2).
Можно также определить плотность распределения
,
которая характеризует плотность распределения случайной величины в данной точке. Эта характеристика применяется в случае непрерывного распределения данных.
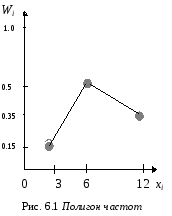
Для наглядности строят различные функции распределения, в частности полигон и гистограмму. Полигоном частот назовем ломаную, отрезки которой соединяют точки (х1, n1), (х2, n2) ,..., (хк, nк), а если вместо nк взяты Wк, то тогда говорят о полигоне относительных частот. (рис. 6.1, данные взяты из примера). В случае непрерывного признака строят гистограмму, для чего весь интервал наблюдений разбивается на несколько частичных подынтервалов шириной h и находят для каждого подынтервала nк сумму частот вариант, попавших в данный интервал.
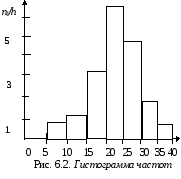
Гистограммой частот будем называть ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные отрезки длиной в h, а высоты равны отношению nк/h, которое называется плотностью частоты.
На рис. 6.2 изображена гистограмма частот распределения объема 100 для примера, приведенного в табл. 6.1. Заметим попутно, что площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.
Таблица 6.1
-
Частичный интервал длиной h = 5
Сумма частот вариант
Плотность частоты
ni /h
5-10
4
0.8
10-15
6
1.2
15-20
16
3.2
20-25
36
7.2
25-30
24
4.8
30-35
10
2.0
35-40
4
0.8
Для построения гистограммы на оси 0x (абсцисс) откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси 0x на расстоянии nк/h. Иными словами строят прямоугольники со сторонами xi, nк / h. Если по оси ординат откладывают относительные частоты, то тогда говорят о построении гистограммы относительных частот.
Другой важной характеристикой распределения является дисперсия - мера разброса отдельных значений относительно среднего значения. Квадратный корень из дисперсии называют стандартным отклонением. Эти величины обозначаются соответственно D и s.
Вычисляют эти характеристики по формулам:
.