Вычисл. матем. (курсовые ИТ-101) / Вычислительная математика / Полезные книги для выполнения курсовой / Эффективные алгоритмы выч матем / glava4_1 / GLAV42

§ 2. Приближенное решение обыкновенного дифференциального уравнения методом Эйлера с уточнением

Другой модификацией этого же метода яв­ля­ет­ся не­ли­нейная вычислительная схема: зная пре­ды­дущее зна­че­ние у_i, вычисляют у ^~_i+1 как у ^~_i+1 = у_i + h у_i , а затем опре­деляют поправку к ре­ше­нию D у ^~ _i+1 по формуле D у ^~_i+1 = f(х_i+1, у_i+1) . Решение находится из уравнения

у_i+1 = у_i + h/2^. [ f(х_i,у_i) + D у ^~_i+1 ] .

Эту вычислительную схему еще называют методом Эйлера - Ко­ши.

Другая вычислительная схема, которую называют ме­­тодом Эйлера с упорядочением решения, заключается в том, что каждое значение у_i+1 = у(х_i+1), где у(х) - ис­ко­мое решение, а х _i+1 = х₀ + h^. (I+1), i = 0, 1, ..., N, оп­ре­де­ля­ется по сле­ду­ю­щей схеме:

1) за начальное приближение берется

,

2) найденное значение уточняется по формуле

, где i = 1, 2, ..., N;

3) уточнение продолжают до тех пор, пока в пре­де­лах тре­буемой точности (заранее заданной) два по­сле­до­ва­тель­ных приближения не совпадут, т.е.

,

где e - погрешность или любое малое число. После этого полагают у_k+1 = у_k+1^-(i), где у_k+1^-(i) общая часть по­лу­чен­но­го ряда ре­шений у_k+1⁽ⁱ⁾.

Иногда описанная выше схема называется ме­то­дом Эйлера с итерационным уточнением ре­ше­ния.

Если после трех итераций решения в пределах тре­бу­е­мой погрешности не совпали, то следует либо умень­шить шаг, либо увеличить погрешность.

В заключение краткого обзора отметим, что метод Эй­лера с итерационным уточнением на­и­бо­лее часто при­меняется в вычислительной прак­ти­ке, так как дает по­грешность порядка h² , т.е. от­но­сится к методам вто­ро­го порядка, несмотря на то, что сам метод Эйлера яв­ля­ется методом пер­во­го порядка.

При решении обыкновенных диф­фе­ре­н­ци­аль­ных урав­нений методом Эйлера с ите­ра­ци­он­ны­м уточ­не­ни­ем значения у_k+1 удобно пользоваться под­про­грам­мой-функцией, формальные значения па­раметров ко­то­рой не приводятся в виду прос­то­ты и понятности пред­ла­гаемой процедуры:

function eyler ( x,y,h,eps : real) : real;

var yk, y0 : real;

dn : boolean;

begin

dn := false;

y0 := y + func (x,y) * h;

repeat

yk := y + func (x,y0) * h * 0.5;

if abs ( yk - y0) < eps then

dn := true;

y0 := yk;

until dn;

eyler := y0;

end.

В подпрограмме-функции eyler исполь­зу­ется про­це­­ду­ра-функция func(х,у) для вы­чис­ления правой час­ти за­да­чи. Ее следует составлять для каждого случая от­дель­но.

Для проверки и тестирования процедуры сос­та­вим таб­ли­цу приближенных зна­чений интеграла диффе­рен­ци­аль­ного урав­не­ния у' = х + соs (0.7 - у) на отрезке [0.7; 1.7] с ша­гом h= 0.1, удовлетворяющего начальным ус­ло­ви­ям у₀(0.7) = =1.1, используя метод Эйлера с уточ­нением. Все вы­чис­ле­ния произведем с точ­нос­тью 10^-5.

Процедура-функция, по которой вычисляется пра­вая часть уравнения, выглядит:

function func (x,y: real) : real;

begin

func := x + cos (0.7 * y);

end;

Результаты работы программы приводятся в табл. 4.2.

Таблица 4.2

Решение дифференциального уравнения у' = х + соs (0.7 - у)
при h = 0.1		при h = 0.05
x = 0.70000	y = 1.100000	x = 0.700000	y = 1.100000
		x = 0.750000	y = 1.135017
x = 0.80000	y = 1.169169	x = 0.800000	y = 1.170830
		x = 0.850000	y = 1.207420
x = 0.90000	y = 1.241447	x = 0.900000	y = 1.244765
		x = 0.950000	y = 1.282844
x = 1.000000	y = 1.316671	x = 1.000000	y = 1.321637
		x = 1.050000	y = 1.361123
x = 1.100000	y = 1.394676	x = 1.100000	y = 1.401280
		x = 1.150000	y = 1.442088
x = 1.200000	y = 1.475300	x = 1.200000	y = 1.483526
		x = 1.250000	y = 1.525575
х = 1.300000	y = 1.558385	x = 1.300000	y = 1.568215
		x = 1.350000	y = 1.611427
x = 1.400000	y = 1.643779	x = 1.400000	y = 1.655191
		x = 1.450000	y = 1.699491
x = 1.500000	y = 1.731338	x = 1.500000	y = 1.744308
		x = 1.550000	y = 1.789626
x = 1.600000	y = 1.820929	x = 1.600000	y = 1.835429
		x = 1.650000	y = 1.881701
x = 1.700000	y = 1.912428	x = 1.700000	y = 1.928429
		x = 1.750000	y = 1.975598

§ 3. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ МЕТОДОМ АДАМСА

Если дифференциальное уравнение у'= f(х, у) име­­ет в правой части сложное ана­ли­ти­чес­кое вы­ра­же­ние, то тог­­да применяют экст­ра­по­ля­ционный ме­тод Адамса, ко­то­рый не требует мно­го­крат­но­го подсчета правой час­ти.

Пусть для дифференциального уравнения зада­ны на­­чаль­ные условия х = х₀ , у = у₀. Требуется най­ти ре­ше­­ние уравнения у' = f(х, у) на отрезке [а, b].

Разобьем отрезок [а, b] равномерно на n частей точ­ка­­­ми х_i = х₀ + h^.i, i = 0, 1, ..., n, h = (b - а)/n. Выберем про­­из­воль­но элементарный отрезок, на котором про­ин­тегрируем диф­ференциальное уравнение

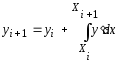_или .

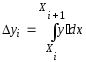Для нахождения производной воспользуемся вто­рой ин­терполяционной формулой Ньютона, ог­ра­ни­чив­шись разностями третьего порядка с уче­том t = (х - х_i)/h:

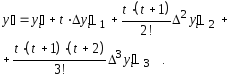
Подставим полученное выражение для у' в ин­те­­граль­ное уравнение и, учитывая, что dх = hdt, име­ем

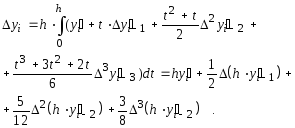
Обозначим через q_i = у_i'; h = f(х_i, у_i)^.h, , тог­да для любой разности D^m q_i = D^m (у_i'h) имеем вы­ражение

Dy_i = q_i + 1/2 ^. Dq_i-1 + 5/12 ^. D²q_i-2 + 3/8 ^. D³q_i-3,

используемое для получения решения урав­нения

у_i+1 = у_i + Dу_i.

Две по­­след­ние формулы яв­ля­ют­ся основными в эк­стра­по­ля­ци­он­ном методе Адам­са.

Схема предлагается из работы [Численные ..., 1976]. Для начала процесса вычисления нужны четыре на­чаль­ных значения у₀, у₁, у₂ и у_3, которые мож­но опре­де­лить любым известным методом. Далее, зная у₀, у₁, у₂ и у₃ , находят q₀ = =hy₀’ = h f(x₀, y₀); q₂ = hy₂’ = h f(x₂, y₂); q₃ = hy₃’ =h f(x₃, y₃); q₄ = hy₄’ = h f(x₄, y₄) и составляют таблицу конечных раз­нос­тей ве­личин q (табл. 4.3)

Таблица 4.3

№ п/п

xi

yi

Dyi

yi’=f(x0,y0)

qi = hyi’

Конечные разности

0

x0

y0

f(x0,y0)

—

—

—

—

1

x1

y1

f(x1,y1)

q0

Dq0

D^2q0

D^3q0

2

x2

y2

f(x2,y2)

q1

Dq1

D^2q1

3

x3

y3

Dy3

f(x3,y3)

q2

Dq2

4

x4

y4

f(x4,y4)

q3

5

x4

y5

...

...

...

...

...

Метод Адамса заключается в продолжении дан­ной таб­ли­цы разностей с помощью формулы для Dу_i. Ис­поль­зуя уже вычисленные q₃, Dq₂, D²q₁ и D³q₀, рас­по­ло­жен­ные в таб­­лице диагонально, по формуле для Dу_i по­лу­чают, по­ла­гая n = 3,

Dу₃ = q₃ + 0.5Dq₂ + (5/12) ^. D²q₁ + (3/8) ^. D³q₀ ,

Dу₃ вносят в таблицу и находят у₄ = у₃+Dу₃. Затем, ис­поль­зуя х₄ и у₄ находят f(х₄,у₄), q₄, Dq₃, D ²q₂ и D³q₁, т.е. новую ди­­а­го­наль. По этим данным опре­деляют значение Dу₄, ко­то­рое тут же вно­сят в таб­ли­цу, и находят у₅ = у₄ + Dу₄.

Таблицу продолжают по описанному алгоритму до ее за­пол­­не­ния, вычисляя правую часть формулы при этом толь­ко один раз. Что­бы оценить погрешность по­лу­­чен­но­го результата, можно применить правило Рун­­ге или просто следить за третьими разностями D³q_i, ко­то­рые считаются по­сто­ян­ны­ми. Этого мож­но добиться, вы­­бирая h каждый раз та­кой, что­­бы выражение для оценки погрешности бы­ло |D³q_i-1 - D³q_i| < e. На практике h выбирают из не­ра­вен­ст­ва h⁴ < e, где e - за­данная точность ре­ше­ния.

Метод Рунге состоит в том, что сначала находится ре­шение диф­фе­рен­ци­аль­но­го уравнения при шаге h, а за­тем зна­че­ние h удва­и­ва­ет­ся и находится решение при но­­вом шаге. Погрешность оце­нивается по формуле

e = (2^m - 1) ^. |y_n^~ - y^~_2n| ,

где y_n^~ - значение приближенного вычисления при двойном шаге; m - порядок метода.

Процедура, реализующая указанную схе­му, может быть следующей:

prоcedure adams (a,b,h,eps,yn : real;

var yi:mas1);

type mas = array [1..20] of real;

var x0, y0, y : real; ff : text; i : integer;

xi, dyi, ysh, qi, dqi, d2qi, d3qi : mas;

83