Жданов С.К Цветков И.В - Основы физических процессов в плазме и в плазменных установках (2000)

§ 23. Ɇɚɝɧɢɬɧɨɟ ɞɚɜɥɟɧɢɟ

ȼɟɫɶɦɚ ɜɚɠɧɵɟ ɜɵɜɨɞɵ ɨɛɳɟɝɨ ɯɚɪɚɤɬɟɪɚ ɦɨɝɭɬ ɛɵɬɶ ɩɨɥɭɱɟɧɵ ɧɟɩɨɫɪɟɞɫɬɜɟɧɧɨ ɢɡ ɚɧɚɥɢɡɚ ɭɪɚɜɧɟɧɢɣ (3.4) ɢ&(3.5).

ȼ ɩɪɟɧɟɛɪɟɠɟɧɢɢ ɜɧɟɲɧɢɦɢ ɫɢɥɚɦɢ F , ɞɜɢɠɟɧɢɟ ɩɥɚɡɦɵ ɨɩɪɟɞɟɥɹɟɬɫɹ ɫɢɥɨɣ Ⱥɦɩɟɪɚ (ɢɧɚɱɟ ɧɚɡɵɜɚɟɦɨɣ ɩɨɧɞɟɪɨɦɨɬɨɪɧɨɣ ɫɢɥɨɣ) ɢ ɝɪɚɞɢɟɧɬɨɦ ɝɚɡɨɤɢɧɟɬɢɱɟɫɤɨɝɨ ɞɚɜɥɟɧɢɹ

	dv&	1 &			&
ρ		=		j	× B − p .	(3.11)
	dt		c

ɂɫɩɨɥɶɡɭɹ ɢɡɜɟɫɬɧɨɟ ɬɨɠɞɟɫɬɜɨ ɢɡ ɜɟɤɬɨɪɧɨɝɨ ɚɧɚɥɢɡɚ, ɫɩɪɚɜɟɞɥɢɜɨɟ ɞɥɹ ɞɜɭɯ

&

&

ɥɸɛɵɯ ɜɟɤɬɨɪɨɜ a ɢ b ,

&

&

&

&

&&

&

&

( ab )=( a )b

+( b

)a

+ a × rotb + b × rota ,

ɢ ɭɪɚɜɧɟɧɢɟ (3.6), ɩɨɧɞɟɪɨɦɨɬɨɪɧɭɸ ɫɢɥɭ ɦɨɠɧɨ ɩɪɟɞɫɬɚɜɢɬɶ ɜ ɜɢɞɟ:

1

&j × B& =

1

rotB& × B& = −

B2

+

1

( B& )B&≡ − pɦɚɝ .

(3.12)

4π

c

8π

4π

ɝɞɟ

pɦɚɝ =

B

2

^

(δ −

2ττ ),

(3.13)

8π

&

ɬɟɧɡɨɪ ɦɚɝɧɢɬɧɨɝɨ ɞɚɜɥɟɧɢɹ;

δ

- ɟɞɢɧɢɱɧɚɹ ɦɚɬɪɢɰɚ, ɚ τ& =

B

− ɟɞɢɧɢɱɧɵɣ

B

ɜɟɤɬɨɪ, ɧɚɩɪɚɜɥɟɧɧɵɣ ɩɨ ɤɚɫɚɬɟɥɶɧɨɣ ɤ ɫɢɥɨɜɨɣ ɥɢɧɢɢ ɦɚɝɧɢɬɧɨɝɨ& ɩɨɥɹ. ȼ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ ɫ ɨɫɶɸ z, ɧɚɩɪɚɜɥɟɧɧɨɣ ɜɞɨɥɶ ɜɟɤɬɨɪɚ B , ɷɬɨɬ ɬɟɧɡɨɪ ɡɚɩɢɫɵɜɚɟɬɫɹ ɜ ɜɢɞɟ ɫɥɟɞɭɸɳɟɣ ɞɢɚɝɨɧɚɥɶɧɨɣ ɬɚɛɥɢɰɵ:

		§	B	2		0		0		·
		¨								¸
			8π
		¨				B2				¸
p		= ¨	0					0		¸ .	(3.14)
						8π
	ɦɚɝ	¨								¸
		¨	0			0	−		B2 ¸
		©							8π ¹
		¨								¸

Ɂɧɚɤ ɤɨɦɩɨɧɟɧɬ ɬɟɧɡɨɪɚ ɦɚɝɧɢɬɧɨɝɨ ɞɚɜɥɟɧɢɹ ɧɟ ɫɥɭɱɚɟɧ: ɩɨɩɟɪɟɱɧɵɟ ɤɨɦɩɨɧɟɧɬɵ ɩɨɥɨɠɢɬɟɥɶɧɵ, ɱɬɨ ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɪɚɫɬɚɥɤɢɜɚɧɢɸ ɫɢɥɨɜɵɯ ɥɢɧɢɣ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɜ ɩɨɩɟɪɟɱɧɨɦ ɧɚɩɪɚɜɥɟɧɢɢ, ɬɨɝɞɚ ɤɚɤ ɩɪɨɞɨɥɶɧɚɹ ɤɨɦɩɨɧɟɧɬɚ ɷɬɨɝɨ ɬɟɧɡɨɪɚ ɨɬɪɢɰɚɬɟɥɶɧɚ − ɜ ɩɪɨɞɨɥɶɧɨɦ ɧɚɩɪɚɜɥɟɧɢɢ ɫɢɥɨɜɵɟ ɥɢɧɢɢ ɧɚɬɹɧɭɬɵ.

ȼɟɥɢɱɢɧɭ

	pm =	B2	(3.15)
		8π

ɨɛɵɱɧɨ ɧɚɡɵɜɚɸɬ ɦɚɝɧɢɬɧɵɦ ɞɚɜɥɟɧɢɟɦ.

ɉɨɥɟɡɧɨ ɬɚɤ ɩɟɪɟɩɢɫɚɬɶ ɫɨɨɬɧɨɲɟɧɢɟ (3.12), ɱɬɨɛɵ ɪɚɫɬɚɥɤɢɜɚɧɢɟ ɢ ɧɚɬɹɠɟɧɢɟ ɫɢɥɨɜɵɯ ɥɢɧɢɣ ɩɪɨɹɜɥɹɥɢɫɶ ɜ ɧɟɦ ɟɳɟ ɛɨɥɟɟ ɹɜɧɨ. Ⱦɥɹ ɷɬɨɝɨ, ɩɨɥɶɡɭɹɫɶ ɨɩɪɟɞɟɥɟɧɢɟɦ ɤɚɫɚɬɟɥɶɧɨɝɨ

ɜɟɤɬɨɪɚ, ɡɚɩɢɲɟɦ

( B& )B& = ( Bτ& )( Bτ&) = B2 (τ& )τ&+ Bτ&(τ& B ).

ɍɱɢɬɵɜɚɹ, ɞɚɥɟɟ, ɱɬɨ ɩɨ ɨɩɪɟɞɟɥɟɧɢɸ

(τ& )τ& = n& , R

ɝɞɟ n - ɧɨɪɦɚɥɶ ɤ ɫɢɥɨɜɨɣ ɥɢɧɢɢ, ɚ R - ɪɚɞɢɭɫ ɟɟ ɤɪɢɜɢɡɧɵ, ɩɨɥɭɱɢɦ

1 &		&	B2		B2 &
	j	× B = −		+		n ,	(3.16)
c			8π		4πR

ɝɞɟ ɨɛɨɡɧɚɱɟɧɨ ɞɥɹ ɤɪɚɬɤɨɫɬɢ

= − τ (τ ) .

ɉɟɪɜɨɟ ɫɥɚɝɚɟɦɨɟ ɜ (3.16) ɨɬɜɟɱɚɟɬ ɮɚɪɚɞɟɟɜɫɤɨɦɭ “ɪɚɫɬɚɥɤɢɜɚɧɢɸ”, ɚ ɜɬɨɪɨɟ, ɫɜɹɡɚɧɧɨɟ ɫ ɢɫɤɪɢɜɥɟɧɢɟɦ ɦɚɝɧɢɬɧɨɣ ɫɢɥɨɜɨɣ ɥɢɧɢɢ, ɨɩɢɫɵɜɚɟɬ ɜɥɢɹɧɢɟ ɧɚɬɹɠɟɧɢɹ ɦɚɝɧɢɬɧɵɯ ɫɢɥɨɜɵɯ ɥɢɧɢɣ, ɢɥɢ ɮɚɪɚɞɟɟɜɫɤɨɟ “ɫɨɤɪɚɳɟɧɢɟ ɞɥɢɧɵ”. ɉɨɞɱɟɪɤɧɟɦ, ɱɬɨ ɜ ɜɚɤɭɭɦɟ, ɬɨ ɟɫɬɶ ɜ ɨɛɥɚɫɬɢ ɜɧɟ ɬɨɤɨɜ, ɤɨɝɞɚ &j ≡ 0 , ɢɡ (3.16) ɫɥɟɞɭɟɬ ɫɨɨɬɧɨɲɟɧɢɟ

B = n& , B R

ɤɨɬɨɪɨɟ ɭɠɟ ɢɫɩɨɥɶɡɨɜɚɥɨɫɶ ɧɚɦɢ ɪɚɧɟɟ ɩɪɢ ɨɛɫɭɠɞɟɧɢɢ ɞɪɟɣɮɨɜɨɝɨ ɞɜɢɠɟɧɢɹ ɱɚɫɬɢɰ ɩɥɚɡɦɵ ɜ ɧɟɨɞɧɨɪɨɞɧɨɦ ɦɚɝɧɢɬɧɨɦ ɩɨɥɟ. Ɉɛɟ ɮɨɪɦɵ ɡɚɩɢɫɢ (3.12) ɢ (3.16) ɜɩɨɥɧɟ ɪɚɜɧɨɡɧɚɱɧɵ, ɢ ɦɨɠɧɨ ɩɨɥɶɡɨɜɚɬɶɫɹ ɥɸɛɨɣ ɢɡ ɧɢɯ.

Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɩɨɧɞɟɪɨɦɨɬɨɪɧɚɹ ɫɢɥɚ ɦɨɠɟɬ ɛɵɬɶ ɩɪɟɞɫɬɚɜɥɟɧɚ ɜ ɜɢɞɟ ɫɭɦɦɵ ɝɪɚɞɢɟɧɬɚ ɦɚɝɧɢɬɧɨɝɨ ɞɚɜɥɟɧɢɹ ɢ ɤɨɦɩɨɧɟɧɬɵ, ɨɛɹɡɚɧɧɨɣ ɫɜɨɟɦɭ ɩɨɹɜɥɟɧɢɸ ɧɚɬɹɠɟɧɢɸ ɦɚɝɧɢɬɧɵɯ ɫɢɥɨɜɵɯ ɥɢɧɢɣ. ȼ ɨɞɧɨɪɨɞɧɨɦ ɩɨɥɟ ɢɦɟɟɦ R→∞, ɢ ɜɤɥɚɞ ɨɬ ɷɬɨɣ ɤɨɦɩɨɧɟɧɬɵ ɨɛɪɚɳɚɟɬɫɹ ɜ ɧɭɥɶ.

ȼ ɩɪɨɛɥɟɦɟ ɦɚɝɧɢɬɧɨɝɨ ɭɞɟɪɠɚɧɢɹ ɩɥɚɡɦɵ ɜɚɠɧɭɸ ɪɨɥɶ ɢɝɪɚɟɬ ɩɚɪɚɦɟɬɪ

β =	p	=	8πp	,	(3.17)
	pm		B2

ɨɩɪɟɞɟɥɹɸɳɢɣ ɨɬɧɨɲɟɧɢɟ ɝɚɡɨɤɢɧɟɬɢɱɟɫɤɨɝɨ ɞɚɜɥɟɧɢɹ ɩɥɚɡɦɵ ɤ ɦɚɝɧɢɬɧɨɦɭ ɞɚɜɥɟɧɢɸ. ȼ ɡɚɜɢɫɢɦɨɫɬɢ ɨɬ ɜɟɥɢɱɢɧɵ ɷɬɨɝɨ ɩɚɪɚɦɟɬɪɚ ɩɪɢɧɹɬɨ ɝɨɜɨɪɢɬɶ ɨ

ɩɥɚɡɦɟ ɜɵɫɨɤɨɝɨ ɞɚɜɥɟɧɢɹ, ɟɫɥɢ β>1, ɢɥɢ ɨ ɩɥɚɡɦɟ ɧɢɡɤɨɝɨ ɞɚɜɥɟɧɢɹ, ɟɫɥɢ β<1.

ɇɚɩɪɢɦɟɪ, ɜ ɬɨɤɚɦɚɤɚɯ ɩɪɢɧɰɢɩɢɚɥɶɧɨ ɦɨɠɟɬ ɭɞɟɪɠɢɜɚɬɶɫɹ ɬɨɥɶɤɨ ɩɥɚɡɦɚ ɧɢɡɤɨɝɨ ɞɚɜɥɟɧɢɹ, βmax<0.1. ȼ ɬɨ ɜɪɟɦɹ ɤɚɤ ɜ ɨɬɤɪɵɬɵɯ ɥɨɜɭɲɤɚɯ ɜ ɩɪɢɧɰɢɩɟ ɜɨɡɦɨɠɧɨ ɭɞɟɪɠɚɧɢɟ ɩɥɚɡɦɵ ɫ β ~1.

Ɉɬɦɟɬɢɦ ɜ ɡɚɤɥɸɱɟɧɢɟ, ɱɬɨ, ɬɚɤ ɤɚɤ ɦɚɝɧɢɬɧɨɟ ɞɚɜɥɟɧɢɟ, ɨɩɪɟɞɟɥɟɧɧɨɟ ɮɨɪɦɭɥɨɣ (3.15), ɹɜɥɹɟɬɫɹ ɨɞɧɨɜɪɟɦɟɧɧɨ ɢ ɩɥɨɬɧɨɫɬɶɸ ɦɚɝɧɢɬɧɨɣ ɷɧɟɪɝɢɢ, ɬɨ pm ɢɡɦɟɪɹɟɬɫɹ ɜ ɷɪɝ/ɫɦ3, ɟɫɥɢ ɦɚɝɧɢɬɧɚɹ ɢɧɞɭɤɰɢɹ ȼ ɢɡɦɟɪɹɟɬɫɹ ɜ ɝɚɭɫɫɚɯ.

§ 24. Ɋɚɜɧɨɜɟɫɢɟ ɩɥɚɡɦɵ ɜ ɦɚɝɧɢɬɧɨɣ ɝɢɞɪɨɞɢɧɚɦɢɤɟ

ȼɚɠɧɵɣ ɤɪɭɝ ɡɚɞɚɱ, ɜ ɤɨɬɨɪɵɯ ɫ ɭɫɩɟɯɨɦ ɩɪɢɦɟɧɹɟɬɫɹ ɦɚɝɧɢɬɧɚɹ ɝɢɞɪɨɞɢɧɚɦɢɤɚ, ɫɜɹɡɚɧ ɫɨ ɫɬɚɰɢɨɧɚɪɧɵɦɢ ɬɟɱɟɧɢɹɦɢ ɩɥɚɡɦɵ, ɬ.ɟ. ɫ ɬɚɤɢɦɢ, ɤɨɝɞɚ ɩɚɪɚɦɟɬɪɵ ɬɟɱɟɧɢɹ ɹɜɧɨ ɧɟ ɡɚɜɢɫɹɬ ɨɬ ɜɪɟɦɟɧɢ ɢ ɱɚɫɬɧɵɟ ɩɪɨɢɡɜɨɞɧɵɟ ɩɨ ɜɪɟɦɟɧɢ ɜ ɭɪɚɜɧɟɧɢɹɯ (3.4) − (3.10) ɦɨɠɧɨ ɨɩɭɫɬɢɬɶ. ɑɚɫɬɧɵɦ ɫɥɭɱɚɟɦ ɫɬɚɰɢɨɧɚɪɧɵɯ ɩɪɨɰɟɫɫɨɜ ɹɜɥɹɸɬɫɹ ɫɬɚɬɢɱɟɫɤɢɟ ɪɚɜɧɨɜɟɫɢɹ, ɤɨɝɞɚ ɫɤɨɪɨɫɬɶ ɩɥɚɡɦɵ ɬɨɠɞɟɫɬɜɟɧɧɨ ɪɚɜɧɚ ɧɭɥɸ. ɗɬɨ ɢɦɟɧɧɨ ɪɚɜɧɨɜɟɫɢɹ, ɬɚɤ ɤɚɤ ɢɡ ɭɫɥɨɜɢɹ v& = 0 ɜɵɬɟɤɚɟɬ dv&dt = 0 , ɚ, ɫɥɟɞɨɜɚɬɟɥɶɧɨ, ɞɟɣɫɬɜɭɸɳɢɟ ɧɚ ɥɸɛɨɣ ɷɥɟɦɟɧɬɚɪɧɵɣ ɨɛɴɟɦ ɩɥɚɡɦɵ ɫɢɥɵ ɞɨɥɠɧɵ ɛɵɬɶ ɭɪɚɜɧɨɜɟɲɟɧɵ. ɉɪɢ ɷɬɨɦ, ɤɚɤ ɷɬɨ ɜɢɞɧɨ ɢɡ ɭɪɚɜɧɟɧɢɹ ɞɜɢɠɟɧɢɹ (3.5), ɞɨɥɠɧɨ ɛɵɬɶ ɜɵɩɨɥɧɟɧɨ ɭɫɥɨɜɢɟ:

1 &		&
	j	× B = p .	(3.18)
c

ɗɬɨ ɭɫɥɨɜɢɟ ɢ ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɭɪɚɜɧɟɧɢɟ ɪɚɜɧɨɜɟɫɢɹ& ɩɥɚɡɦɵ ɜ ɦɚɝɧɢɬɧɨɣ ɝɢɞɪɨɞɢɧɚɦɢɤɟ. ɂɡ ɧɟɝɨ, ɨɱɟɜɢɞɧɨ, ɫɥɟɞɭɟɬ, ɱɬɨ ɜɟɤɬɨɪɚ &j ɢ B ɥɟɠɚɬ ɧɚ ɩɨɜɟɪɯɧɨɫɬɹɯ, ɨɪɬɨɝɨɧɚɥɶɧɵɯ ɤ ɝɪɚɞɢɟɧɬɭ ɞɚɜɥɟɧɢɹ, ɬɨ ɟɫɬɶ ɧɚ ɩɨɜɟɪɯɧɨɫɬɹɯ ɩɨɫɬɨɹɧɧɨɝɨ ɞɚɜɥɟɧɢɹ p=const. ɋ ɞɪɭɝɨɣ ɫɬɨɪɨɧɵ, ɟɫɥɢ ɦɚɝɧɢɬɧɨɣ ɤɨɧɮɢɝɭɪɚɰɢɢ ɫɨɩɨɫɬɚɜɢɬɶ ɫɟɦɟɣɫɬɜɨ ɦɚɝɧɢɬɧɵɯ ɩɨɜɟɪɯɧɨɫɬɟɣ, ɧɚ ɤɨɬɨɪɵɯ ɥɟɠɚɬ ɫɢɥɨɜɵɟ ɥɢɧɢɢ, ɬɨ, ɨɱɟɜɢɞɧɨ, ɱɬɨ ɢɦɟɧɧɨ ɧɚ ɷɬɢɯ ɩɨɜɟɪɯɧɨɫɬɹɯ ɞɚɜɥɟɧɢɟ ɩɥɚɡɦɵ ɞɨɥɠɧɨ ɛɵɬɶ ɩɨɫɬɨɹɧɧɨ. Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɦɚɝɧɢɬɧɵɟ ɩɨɜɟɪɯɧɨɫɬɢ ɭɞɟɪɠɢɜɚɸɳɟɝɨ ɩɥɚɡɦɭ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɫ ɧɟɨɛɯɨɞɢɦɨɫɬɶɸ ɞɨɥɠɧɵ ɛɵɬɶ ɢɡɨɛɚɪɢɱɟɫɤɢɦɢ ɞɥɹ ɩɥɚɡɦɵ.

ȼ ɩɪɨɫɬɟɣɲɟɦ ɫɥɭɱɚɟ, ɤɨɝɞɚ ɫɢɥɨɜɵɟ ɥɢɧɢɢ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɹɜɥɹɸɬɫɹ ɩɪɹɦɨɥɢɧɟɣɧɵɦɢ ɢ ɩɚɪɚɥɥɟɥɶɧɵɦɢ ɞɪɭɝ ɞɪɭɝɭ, ɢɯ ɪɚɞɢɭɫ ɤɪɢɜɢɡɧɵ ɪɚɜɟɧ ɛɟɫɤɨɧɟɱɧɨɫɬɢ, ɬɨ ɫɨɝɥɚɫɧɨ ɜɵɪɚɠɟɧɢɸ (3.16) ɦɨɠɧɨ ɡɚɩɢɫɚɬɶ

1 &		&	B2
	j	× B = −		.	(3.19)
c			8π

ȼɵɛɪɚɜ ɧɚɩɪɚɜɥɟɧɢɟ ɫɢɥɨɜɵɯ ɥɢɧɢɣ ɡɚ ɨɫɶ z ɫɢɫɬɟɦɵ ɤɨɨɪɞɢɧɚɬ, ɞɥɹ ɟɞɢɧɫɬɜɟɧɧɨɣ ɨɬɥɢɱɧɨɣ ɨɬ& ɧɭɥɹ ɤɨɦɩɨɧɟɧɬɵ ɩɨɥɹ Bz ɢɡ ɭɪɚɜɧɟɧɢɹ ɫɨɥɟɧɨɢɞɚɥɶɧɨɫɬɢ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ

div B = 0

ɩɨɥɭɱɢɦ

∂

∂ z Bz = 0 ,

ɢ ɦɚɝɧɢɬɧɚɹ ɢɧɞɭɤɰɢɹ ɦɨɠɟɬ ɦɟɧɹɬɶɫɹ ɬɨɥɶɤɨ ɩɨɩɟɪɟɤ ɧɚɩɪɚɜɥɟɧɢɹ ɫɢɥɨɜɵɯ ɥɢɧɢɣ. ȼɨɫɩɨɥɶɡɨɜɚɜɲɢɫɶ ɩɪɟɞɫɬɚɜɥɟɧɢɟɦ (3.19) ɞɥɹ ɫɢɥɵ Ⱥɦɩɟɪɚ, ɢɡ ɭɪɚɜɧɟɧɢɹ (3.18) ɩɨɥɭɱɢɦ

	B 2	,	∂	p = 0 ,
8π + p = 0			∂ z
	z

ɫɥɟɞɨɜɚɬɟɥɶɧɨ, ɞɚɜɥɟɧɢɟ ɩɥɚɡɦɵ ɬɚɤɠɟ ɧɟ ɦɟɧɹɟɬɫɹ ɜɞɨɥɶ ɫɢɥɨɜɵɯ ɥɢɧɢɣ, ɚ ɩɨɩɟɪɟɤ ɫɢɥɨɜɵɯ ɥɢɧɢɣ ɞɨɥɠɧɚ ɛɵɬɶ ɩɨɫɬɨɹɧɧɚ ɫɭɦɦɚ ɞɚɜɥɟɧɢɹ ɩɥɚɡɦɵ ɢ ɦɚɝɧɢɬɧɨɝɨ ɞɚɜɥɟɧɢɹ:

Bz 2 + p = const . 8π

ɋɨɝɥɚɫɧɨ ɷɬɨɦɭ ɭɫɥɨɜɢɸ ɜɧɟ ɨɛɥɚɫɬɢ, ɡɚɧɹɬɨɣ ɩɥɚɡɦɨɣ, ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ ɹɜɥɹɟɬɫɹ ɨɞɧɨɪɨɞɧɵɦ, ɩɭɫɬɶ ɡɞɟɫɶ Bz=B0. Ɍɨɝɞɚ ɩɨɫɬɨɹɧɧɭɸ ɦɨɠɧɨ ɜɵɛɪɚɬɶ ɬɚɤ, ɱɬɨ ɜɨ ɜɫɟɦ ɩɪɨɫɬɪɚɧɫɬɜɟ ɛɭɞɟɬ

	B	2		B	2
	z		+ p =	0		.	(3.20)
	8π			8π

ȼɢɞɧɨ, ɱɬɨ ɜ ɨɛɥɚɫɬɢ, ɡɚɧɹɬɨɣ ɩɥɚɡɦɨɣ, ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ ɦɟɧɶɲɟ ɜɧɟɲɧɟɝɨ. Ɇɨɠɧɨ ɫɤɚɡɚɬɶ, ɱɬɨ ɩɥɚɡɦɚ «ɜɵɬɚɥɤɢɜɚɟɬ» ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ, ɤɚɤ ɢ ɥɸɛɨɣ ɞɪɭɝɨɣ ɞɢɚɦɚɝɧɟɬɢɤ.

ɍɪɚɜɧɟɧɢɟ (3.20) ɞɥɹ ɪɚɫɫɦɚɬɪɢɜɚɟɦɨɝɨ ɱɚɫɬɧɨɝɨ ɫɥɭɱɚɹ ɭɫɬɚɧɚɜɥɢɜɚɟɬ ɭɫɥɨɜɢɟ ɪɚɜɧɨɜɟɫɧɨɝɨ ɫɨɫɬɨɹɧɢɹ ɫɢɫɬɟɦɵ “ɩɥɚɡɦɚ − ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ”, ɩɪɢɱɟɦ ɞɚɜɥɟɧɢɟ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɜɧɟ ɩɥɚɡɦɵ ɜ ɪɚɜɧɨɜɟɫɢɢ ɞɨɥɠɧɨ ɛɵɬɶ ɛɨɥɶɲɟ ɦɚɝɧɢɬɧɨɝɨ ɞɚɜɥɟɧɢɹ

ɜɧɭɬɪɟɧɧɟɝɨ ɩɨɥɹ ɤɚɤ ɪɚɡ ɧɚ ɜɟɥɢɱɢɧɭ ɝɚɡɨɤɢɧɟɬɢɱɟɫɤɨɝɨ ɞɚɜɥɟɧɢɹ ɩɥɚɡɦɵ, ɱɬɨ ɧɚɝɥɹɞɧɨ ɞɟɦɨɧɫɬɪɢɪɭɟɬ ɢɞɟɸ ɭɞɟɪɠɚɧɢɹ ɩɥɚɡɦɵ ɦɚɝɧɢɬɧɵɦ ɩɨɥɟɦ. ɉɨɞɱɟɪɤɧɟɦ, ɱɬɨ ɜ ɭɪɚɜɧɟɧɢɹɯ ɪɚɜɧɨɜɟɫɢɹ ɧɟɬ ɤɚɤɢɯ-ɥɢɛɨ ɨɝɪɚɧɢɱɟɧɢɣ ɧɚ ɩɪɨɢɫɯɨɠɞɟɧɢɟ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ, ɩɨɷɬɨɦɭ ɨɧɨ ɦɨɠɟɬ ɛɵɬɶ ɫɨɡɞɚɧɨ ɤɚɤ ɜɧɟɲɧɢɦɢ ɬɨɤɚɦɢ, ɬɚɤ ɢ ɬɨɤɨɦ, ɩɪɨɬɟɤɚɸɳɢɦ ɩɨ ɩɥɚɡɦɟ. ȼɦɟɫɬɟ ɫ ɬɟɦ ɭɫɥɨɜɢɟ (3.20) ɫɜɹɡɵɜɚɟɬ ɞɜɟ ɧɟɢɡɜɟɫɬɧɵɟ ɜɟɥɢɱɢɧɵ. ɉɨɷɬɨɦɭ ɞɥɹ ɨɞɧɨɡɧɚɱɧɨɝɨ ɪɟɲɟɧɢɹ ɡɚɞɚɱɢ ɪɚɜɧɨɜɟɫɢɹ ɧɟɨɛɯɨɞɢɦɨ ɩɪɢɜɥɟɤɚɬɶ ɞɨɩɨɥɧɢɬɟɥɶɧɵɟ ɭɫɥɨɜɢɹ, ɜ ɬɨɦ ɱɢɫɥɟ ɭɫɥɨɜɢɹ ɩɨɞɞɟɪɠɚɧɢɹ ɬɨɤɚ ɜ ɩɥɚɡɦɟ.

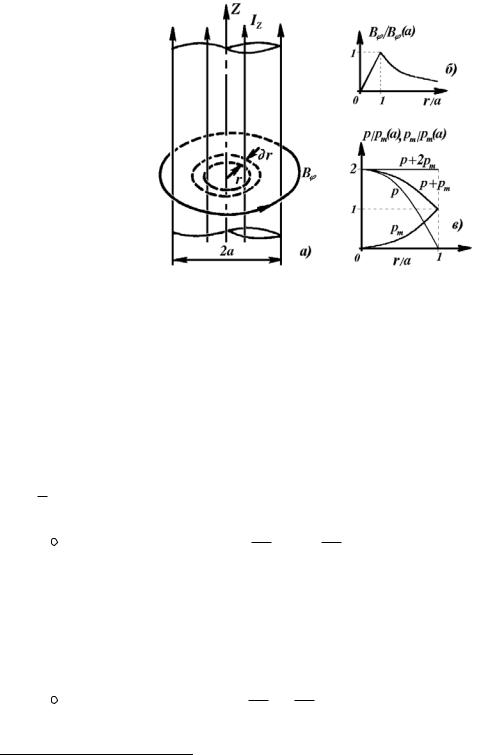
ɉɪɢɦɟɪɨɦ ɤɜɚɡɢɫɬɚɰɢɨɧɚɪɧɨɝɨ ɩɪɨɰɟɫɫɚ ɦɨɠɟɬ ɫɥɭɠɢɬɶ ɪɚɜɧɨɜɟɫɧɨɟ ɫɨɫɬɨɹɧɢɟ ɫɚɦɨɫɠɢɦɚɸɳɟɝɨɫɹ ɞɥɢɧɧɨɝɨ ɰɢɥɢɧɞɪɢɱɟɫɤɨɝɨ ɫɬɨɥɛɚ ɩɥɚɡɦɵ ɫ ɩɪɨɞɨɥɶɧɵɦ ɬɨɤɨɦ - ɬɚɤ

Ɋɢɫ.3.1. ɉɥɚɡɦɟɧɧɵɣ Z-ɩɢɧɱ: ɚ − ɝɟɨɦɟɬɪɢɹ ɬɨɤɨɜɨɝɨ ɤɚɧɚɥɚ, ɛ − ɪɚɫɩɪɟɞɟɥɟɧɢɟ ɦɚɝɧɢɬɧɨɝɨ

ɩɨɥɹ, ɜ −ɞɚɜɥɟɧɢɹ ɩɥɚɡɦɵ (ɪ) ɢ ɦɚɝɧɢɬɧɨɝɨ ɞɚɜɥɟɧɢɹ (pm) ɩɨ ɪɚɞɢɭɫɭ

ɧɚɡɵɜɚɟɦɵɣ Z-ɩɢɧɱ . ȼ ɷɬɨɦ ɫɥɭɱɚɟ ȼ ɢ ɪ ɡɚɜɢɫɹɬ ɬɨɥɶɤɨ ɨɬ ɨɞɧɨɣ ɤɨɨɪɞɢɧɚɬɵ - ɪɚɫɫɬɨɹɧɢɹ r ɨɬ ɨɫɢ ɫɬɨɥɛɚ (ɪɢɫ.3.1). ɍɪɚɜɧɟɧɢɟ ɪɚɜɧɨɜɟɫɢɹ ɩɪɢɦɟɬ ɜɢɞ:

	−	∂p	=	1	j B .
		∂r		c
					z ϕ

ȿɫɥɢ ɫɱɢɬɚɬɶ ɬɨɤ ɩɢɧɱɚ ɪɚɫɩɪɟɞɟɥɟɧɧɵɦ ɪɚɜɧɨɦɟɪɧɨ ɩɨ ɟɝɨ ɫɟɱɟɧɢɸ, ɬɨ jz=const ɢ

2

Bϕ = c πrjz , ɬɚɤ ɤɚɤ ɩɨ ɬɟɨɪɟɦɟ ɨ ɰɢɪɤɭɥɹɰɢɢ

	2π	4π		4π
³Bϕ dlϕ	≡ ³Bϕ rdϕ ≡ Bϕ 2πr =		J( r ) ≡		πr2 jz ,
	0	c		c

ɝɞɟ

r

J( r ) = 2π ³ jz rdr = πr2 jz

0

− ɬɨɤ ɜ ɰɢɥɢɧɞɪɟ ɫ ɪɚɞɢɭɫɨɦ r. Ⱦɥɹ ɨɛɥɚɫɬɢ ɜɧɟ ɩɢɧɱɚ, ɜɧɨɜɶ ɜɨɫɩɨɥɶɡɨɜɚɜɲɢɫɶ ɬɟɨɪɟɦɨɣ ɨ ɰɢɪɤɭɥɹɰɢɢ, ɩɨɥɭɱɚɟɦ:

2π	4π		4π
³Bϕ dlϕ ≡ ³Bϕ rdϕ ≡ Bϕ 2πr =		I ≡		πa2 jz ,
0	c		c

Ɋɚɡɪɹɞ ɫ ɝɟɨɦɟɬɪɢɟɣ Z-ɩɢɧɱɚ ɜɨɡɧɢɤɚɟɬ, ɧɚɩɪɢɦɟɪ, ɩɪɢ ɩɪɨɩɭɫɤɚɧɢɢ ɫɢɥɶɧɨɝɨ ɬɨɤɚ ɱɟɪɟɡ ɝɚɡ ɦɟɠɞɭ ɞɜɭɦɹ ɩɚɪɚɥɥɟɥɶɧɵɦɢ ɷɥɟɤɬɪɨɞɚɦɢ, ɪɚɫɩɨɥɨɠɟɧɧɵɦɢ ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɨ ɨɫɢ z.

ɝɞɟ I - ɩɨɥɧɵɣ ɬɨɤ ɩɢɧɱɚ. Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɪɚɫɩɪɟɞɟɥɟɧɢɟ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɩɢɧɱɚ ɫɥɟɞɭɸɳɟɟ (ɪɢɫ. 3.1,ɛ):

	°­	r	, r ≤ a
B ( r ) = B ( a )®a			,
ϕ	°a		, r > a
	ϕ

¯r

ɝɞɟ

2I Bϕ ( a ) = ca

ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ ɧɚ ɝɪɚɧɢɰɟ ɩɥɚɡɦɵ.

Ɉɬɦɟɬɢɦ ɩɨɩɭɬɧɨ ɩɨɥɟɡɧɭɸ ɩɪɚɤɬɢɱɟɫɤɭɸ ɮɨɪɦɭɥɭ ɞɥɹ ɪɚɫɱɟɬɚ ɜɟɥɢɱɢɧɵ ɷɬɨɝɨ ɩɨɥɹ:

Bϕ ( a ) = 0.2 I[ A ] , [ Ƚɫ] .

a[ ɫɦ]

ɉɨɞɫɬɚɧɨɜɤɚ ɪɚɫɩɪɟɞɟɥɟɧɢɹ ɩɨɥɹ ɜ ɭɪɚɜɧɟɧɢɟ ɪɚɜɧɨɜɟɫɢɹ ɩɪɢɜɨɞɢɬ ɤ ɫɨɨɬɧɨɲɟɧɢɸ

	∂p	= −	2π	j 2r .
	∂r		c2
				z

ɂɧɬɟɝɪɢɪɭɟɦ ɢ, ɭɱɢɬɵɜɚɹ, ɱɬɨ ɧɚ ɝɪɚɧɢɰɟ ɫɬɨɥɛɚ (ɩɪɢ r=a) ɝɚɡɨɤɢɧɟɬɢɱɟɫɤɨɟ ɞɚɜɥɟɧɢɟ ɪɚɜɧɨ ɧɭɥɸ (ɪ=0), ɩɨɥɭɱɚɟɦ

p =

πa2

j2

§

1

−

r2 ·

=

I 2

§

1

−

r2 ·

≡

Bϕ2 ( a ) §

1

−

r2 ·

¨

¸

¨

¸

¨

¸ .

c2

a2

πa2c2

a2

4π

a2

©

¹

©

¹

©

¹

ɉɨɞɱɟɪɤɧɟɦ, ɱɬɨ ɫɭɦɦɚ ɞɚɜɥɟɧɢɣ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɢ ɞɚɜɥɟɧɢɹ ɩɥɚɡɦɵ

	p +	Bϕ2	( r )	=	Bϕ2 ( a ) §		2	−	r2 ·		≠ const
						¨				¸
		8π			8π				a2
						©				¹

ɬɟɩɟɪɶ ɧɟ ɹɜɥɹɟɬɫɹ ɜɟɥɢɱɢɧɨɣ ɩɨɫɬɨɹɧɧɨɣ (ɫɪɚɜɧɢɦ ɫ (3.20)). Ɉɱɟɜɢɞɧɨ, ɷɬɨ ɫɜɹɡɚɧɨ ɫ ɜɤɥɚɞɨɦ ɨɬ ɧɚɬɹɠɟɧɢɹ ɫɢɥɨɜɵɯ ɥɢɧɢɣ, ɤɨɬɨɪɵɟ ɡɞɟɫɶ ɢɦɟɸɬ ɮɨɪɦɭ ɨɤɪɭɠɧɨɫɬɟɣ ɫ ɤɨɧɟɱɧɵɦ ɪɚɞɢɭɫɨɦ ɤɪɢɜɢɡɧɵ. ɉɨɫɬɨɹɧɧɨɣ ɬɟɩɟɪɶ ɹɜɥɹɟɬɫɹ ɜɟɥɢɱɢɧɚ

B2

( r )

B2

( r )

B2

( r )

B2

( a )

p +

ϕ

− ( −

ϕ

) ≡ p +

ϕ

=

ϕ

= const .

8π

8π

4π

4π

ȼɤɥɚɞ ɧɚɬɹɠɟɧɢɹ ɫɢɥɨɜɵɯ ɥɢɧɢɣ ɩɪɢɜɨɞɢɬ ɤ ɬɨɦɭ, ɱɬɨ ɞɚɜɥɟɧɢɟ ɩɥɚɡɦɵ ɜ ɰɟɧɬɪɟ ɬɨɤɨɜɨɝɨ ɤɚɧɚɥɚ ɨɤɚɡɵɜɚɟɬɫɹ ɪɨɜɧɨ ɜɞɜɨɟ ɛɨɥɶɲɟ ɦɚɝɧɢɬɧɨɝɨ ɞɚɜɥɟɧɢɹ ɧɚ ɟɝɨ ɝɪɚɧɢɰɟ. Ɋɚɫɩɪɟɞɟɥɟɧɢɟ ɞɚɜɥɟɧɢɣ ɜ ɬɨɤɨɜɨɦ ɤɚɧɚɥɟ ɩɨɤɚɡɚɧɨ ɧɚ (ɪɢɫ. 3.1,ɜ).

Ɍɚɤ ɤɚɤ p=2nT, ɬɨ, ɜɜɨɞɹ ɩɨɥɧɨɟ ɱɢɫɥɨ ɱɚɫɬɢɰ ɧɚ ɟɞɢɧɢɰɭ ɞɥɢɧɵ ɩɥɚɡɦɟɧɧɨɝɨ ɫɬɨɥɛɚ N (ɬɚɤ ɧɚɡɵɜɚɟɦɨɟ ɩɨɝɨɧɧɨɟ ɱɢɫɥɨ ɱɚɫɬɢɰ) ɢ ɫɱɢɬɚɹ ɬɟɦɩɟɪɚɬɭɪɭ ɩɥɚɡɦɵ Ɍ ɩɨɫɬɨɹɧɧɨɣ, ɨɩɪɟɞɟɥɢɦ

a	I	2
N = 2π ³nr dr =				,
	4c	2	T
0

ɨɬɤɭɞɚ ɩɨɥɭɱɚɟɦ ɫɨɨɬɧɨɲɟɧɢɟ

I 2 4NT = c2 ,

ɢɡɜɟɫɬɧɨɟ ɤɚɤ ɫɨɨɬɧɨɲɟɧɢɟ Ȼɟɧɧɟɬɚ.

ɉɪɢ ɜɵɜɨɞɟ ɷɬɨɝɨ ɫɨɨɬɧɨɲɟɧɢɹ ɧɚɦɢ ɩɪɟɞɩɨɥɚɝɚɥɨɫɶ, ɱɬɨ ɬɟɦɩɟɪɚɬɭɪɚ ɩɥɚɡɦɵ ɩɨɫɬɨɹɧɧɚ. Ɉɞɧɚɤɨ ɩɪɨɜɨɞɢɦɨɫɬɶ ɪɟɚɥɶɧɨɣ ɩɥɚɡɦɵ ɧɟ ɛɟɫɤɨɧɟɱɧɚ, ɢ ɩɨɷɬɨɦɭ ɩɪɨɬɟɤɚɧɢɟ ɬɨɤɚ ɛɭɞɟɬ ɫɨɩɪɨɜɨɠɞɚɬɶɫɹ ɜɵɞɟɥɟɧɢɟɦ ɞɠɨɭɥɟɜɚ ɬɟɩɥɚ ɢ ɧɚɝɪɟɜɨɦ ɩɥɚɡɦɵ. ȿɫɥɢ ɷɬɨɬ ɩɪɨɰɟɫɫ ɫɱɢɬɚɬɶ ɦɟɞɥɟɧɧɵɦ, ɬɨ ɭɫɥɨɜɢɟ ɪɚɜɧɨɜɟɫɢɹ ɦɨɠɧɨ ɫɱɢɬɚɬɶ, ɩɨ ɤɪɚɣɧɟɣ ɦɟɪɟ, ɩɪɢɛɥɢɠɟɧɧɨ ɫɩɪɚɜɟɞɥɢɜɵɦ. ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɟɫɥɢ ɩɪɢ ɩɨɫɬɨɹɧɧɨɦ ɩɨɝɨɧɧɨɦ ɱɢɫɥɟ ɱɚɫɬɢɰ ɬɟɦɩɟɪɚɬɭɪɚ ɛɭɞɟɬ ɪɚɫɬɢ, ɬɨ ɞɥɹ ɨɛɟɫɩɟɱɟɧɢɹ ɪɚɜɧɨɜɟɫɢɹ ɧɟɨɛɯɨɞɢɦɨ ɭɜɟɥɢɱɢɜɚɬɶ ɬɨɤ.

Ɋɢɫ.3.2. Ƚɟɨɦɟɬɪɢɹ ɬɨɪɨɢɞɚɥɶɧɨɝɨ ɜɢɬɤɚ ɩɥɚɡɦɵ

Ʉ ɫɨɠɚɥɟɧɢɸ, ɜ ɨɛɫɭɠɞɚɟɦɨɣ ɜɵɲɟ ɝɟɨɦɟɬɪɢɢ ɪɚɡɪɹɞɚ ɩɪɚɤɬɢɱɟɫɤɢ ɧɟ ɭɞɚɟɬɫɹ ɞɨɜɟɫɬɢ ɩɥɚɡɦɟɧɧɵɣ ɫɬɨɥɛ ɞɨ ɪɚɜɧɨɜɟɫɧɨɝɨ ɫɨɫɬɨɹɧɢɹ, ɬɚɤ ɤɚɤ ɪɹɞ ɩɪɨɰɟɫɫɨɜ ɩɪɢɜɨɞɢɬ ɤ ɧɟɭɫɬɨɣɱɢɜɨɫɬɢ, ɢ ɫɬɨɥɛ ɩɥɚɡɦɵ ɛɵɫɬɪɨ ɪɚɡɪɭɲɚɟɬɫɹ.

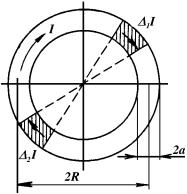
ɉɥɚɡɦɟɧɧɵɣ ɫɬɨɥɛ ɜ Z-ɩɢɧɱɟ ɨɩɢɪɚɟɬɫɹ ɧɚ ɷɥɟɤɬɪɨɞɵ, ɡɧɚɱɢɬ ɜɞɨɥɶ ɫɬɨɥɛɚ ɭɯɨɞ ɱɚɫɬɢɰ ɢ ɩɨɬɟɪɢ ɷɧɟɪɝɢɢ ɜ ɨɛɥɚɫɬɢ ɤɨɧɬɚɤɬɚ ɧɟɢɡɛɟɠɧɵ. ȿɫɬɟɫɬɜɟɧɧɨ ɠɟɥɚɧɢɟ ɫɜɟɪɧɭɬɶ ɫɬɨɥɛ ɩɥɚɡɦɵ ɜ ɬɨɪ − ɫɨɡɞɚɬɶ ɡɚɦɤɧɭɬɭɸ ɛɟɡɷɥɟɤɬɪɨɞɧɭɸ ɫɢɫɬɟɦɭ. Ɉɞɧɚɤɨ ɬɨɪɨɢɞɚɥɶɧɵɣ ɜɢɬɨɤ ɫ ɬɨɤɨɦ ɫɬɪɟɦɢɬɫɹ ɤ ɪɚɫɲɢɪɟɧɢɸ, ɩɨɬɨɦɭ ɱɬɨ ɞɚɜɥɟɧɢɟ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɧɚ ɜɧɭɬɪɟɧɧɸɸ ɩɨɜɟɪɯɧɨɫɬɶ ɜɢɬɤɚ ɛɨɥɶɲɟ, ɱɟɦ ɧɚ ɧɚɪɭɠɧɭɸ. ɇɚɩɪɢɦɟɪ, ɧɚ ɥɸɛɨɣ ɭɱɚɫɬɨɤ ɜɢɬɤɚ ∆1J ɞɟɣɫɬɜɭɟɬ ɨɬɬɚɥɤɢɜɚɸɳɚɹ ɫɢɥɚ ɨɬ ɞɢɚɦɟɬɪɚɥɶɧɨ ɩɪɨɬɢɜɨɩɨɥɨɠɧɨɝɨ ɭɱɚɫɬɤɚ ɜɢɬɤɚ ∆2J (ɪɢɫ.3.2), ɩɨɫɤɨɥɶɤɭ, ɤɚɤ ɢɡɜɟɫɬɧɨ, ɚɧɬɢɩɚɪɚɥɥɟɥɶɧɵɟ ɬɨɤɢ ɨɬɬɚɥɤɢɜɚɸɬɫɹ. ɑɬɨɛɵ ɨɛɟɫɩɟɱɢɬɶ ɪɚɜɧɨɜɟɫɢɟ ɩɥɚɡɦɟɧɧɨɝɨ ɜɢɬɤɚ, ɟɝɨ ɦɨɠɧɨ ɛɵɥɨ ɛɵ ɩɨɦɟɫɬɢɬɶ ɜ ɜɟɪɬɢɤɚɥɶɧɨɟ ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ ȼz, ɧɚɩɪɚɜɥɟɧɧɨɟ ɩɨ ɨɫɢ z, ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɨɣ ɩɥɨɫɤɨɫɬɢ ɜɢɬɤɚ (ɩɥɨɫɤɨɫɬɢ ɪɢɫ.3.2). Ɍɨɝɞɚ ɫɢɥɵ, ɪɚɫɬɹɝɢɜɚɸɳɢɟ ɜɢɬɨɤ F1 J2, ɦɨɝɭɬ ɛɵɬɶ ɫɤɨɦɩɟɧɫɢɪɨɜɚɧɵ ɫɢɥɚɦɢ, ɫɠɢɦɚɸɳɢɦɢ ɟɝɨ, F2 Jȼz. Ɋɚɫɱɟɬɵ [10] ɩɨɤɚɡɵɜɚɸɬ, ɱɬɨ ɩɪɢ ɷɬɨɦ ɪɚɜɧɨɜɟɫɢɟ ɞɨɫɬɢɝɚɟɬɫɹ, ɟɫɥɢ

	J	§	8R		1	·
Bz =		¨ln		−		¸	,
			a		2
	cR ©					¹

ɝɞɟ J - ɩɨɥɧɵɣ ɬɨɤ ɜ ɩɥɚɡɦɟɧɧɨɦ ɜɢɬɤɟ.

Ɋɚɜɧɨɜɟɫɧɨɟ ɫɨɫɬɨɹɧɢɟ ɜɢɬɤɚ ɦɨɠɟɬ ɛɵɬɶ ɩɨɥɭɱɟɧɨ ɬɚɤɠɟ (ɧɚ ɜɪɟɦɟɧɚɯ ɦɚɫɲɬɚɛɚ ɫɤɢɧɨɜɵɯ), ɟɫɥɢ ɟɝɨ ɩɨɦɟɫɬɢɬɶ ɜ ɯɨɪɨɲɨ ɩɪɨɜɨɞɹɳɢɣ ɦɟɬɚɥɥɢɱɟɫɤɢɣ ɤɨɠɭɯ. ɋɦɟɳɟɧɢɟ ɜɢɬɤɚ ɩɪɢɜɨɞɢɬ ɤ ɜɨɡɧɢɤɧɨɜɟɧɢɸ ɬɨɤɨɜ Ɏɭɤɨ ɜ ɤɨɠɭɯɟ, ɢ ɦɚɝɧɢɬɧɵɟ ɩɨɥɹ ɷɬɢɯ ɬɨɤɨɜ ɢɝɪɚɸɬ ɪɨɥɶ ɩɨɥɹ ȼz. ȼ ɷɬɨɦ ɫɥɭɱɚɟ ɜɪɟɦɹ ɫɭɳɟɫɬɜɨɜɚɧɢɹ ɪɚɜɧɨɜɟɫɧɨɝɨ ɫɨɫɬɨɹɧɢɹ ɡɚɜɢɫɢɬ ɨɬ ɫɨɨɬɧɨɲɟɧɢɹ ɪɚɞɢɭɫɚ ɩɥɚɡɦɟɧɧɨɝɨ ɲɧɭɪɚ a, ɪɚɞɢɭɫɚ ɤɚɦɟɪɵ ɬɨɪɚ R, ɩɪɨɜɨɞɢɦɨɫɬɢ ɢ ɬɨɥɳɢɧɵ ∆r ɩɪɨɜɨɞɹɳɟɝɨ ɤɨɠɭɯɚ.

ɋɬɚɛɢɥɢɡɚɰɢɹ ɩɨɥɨɠɟɧɢɹ ɩɥɚɡɦɟɧɧɨɝɨ ɜɢɬɤɚ ɫ ɬɨɤɨɦ ɜɟɪɬɢɤɚɥɶɧɵɦ ɦɚɝɧɢɬɧɵɦ ɩɨɥɟɦ ɢ ɩɪɨɜɨɞɹɳɢɦ ɦɚɫɫɢɜɧɵɦ ɦɟɬɚɥɥɢɱɟɫɤɢɦ ɤɨɠɭɯɨɦ ɪɟɚɥɶɧɨ ɢɫɩɨɥɶɡɨɜɚɥɢɫɶ ɜ ɬɨɤɚɦɚɤɚɯ ɞɥɹ ɨɛɟɫɩɟɱɟɧɢɹ ɪɚɜɧɨɜɟɫɢɹ ɩɨ ɛɨɥɶɲɨɦɭ ɪɚɞɢɭɫɭ ɬɨɪɚ.

Ɋɚɜɧɨɜɟɫɢɟ ɩɨ ɦɚɥɨɦɭ ɪɚɞɢɭɫɭ ɨɛɟɫɩɟɱɢɜɚɟɬɫɹ (ɜ ɫɨɜɨɤɭɩɧɨɫɬɢ ɫ ɩɨɥɟɦ ɬɨɤɚ) ɫɢɥɶɧɵɦ ɬɨɪɨɢɞɚɥɶɧɵɦ ɦɚɝɧɢɬɧɵɦ ɩɨɥɟɦ.

Ɇɚɝɧɢɬɨɝɢɞɪɨɞɢɧɚɦɢɱɟɫɤɢɣ ɦɟɬɨɞ ɪɚɫɫɦɨɬɪɟɧɢɹ ɞɚɟɬ ɜɨɡɦɨɠɧɨɫɬɶ ɤɚɱɟɫɬɜɟɧɧɨ ɢ ɧɚɝɥɹɞɧɨ ɩɪɟɞɫɬɚɜɢɬɶ ɭɫɥɨɜɢɹ ɪɚɜɧɨɜɟɫɢɹ ɩɥɚɡɦɟɧɧɨɝɨ ɲɧɭɪɚ ɪɚɡɥɢɱɧɨɣ ɝɟɨɦɟɬɪɢɢ, ɚ ɪɚɫɱɟɬɵ ɩɨɡɜɨɥɹɸɬ ɨɰɟɧɢɬɶ ɧɟɨɛɯɨɞɢɦɵɟ ɫɨɨɬɧɨɲɟɧɢɹ ɦɚɤɪɨɫɤɨɩɢɱɟɫɤɢɯ ɩɚɪɚɦɟɬɪɨɜ.

§25. Ȼɵɫɬɪɵɟ ɩɪɨɰɟɫɫɵ

ȼɭɪɚɜɧɟɧɢɢ (3.18) ɢɧɟɪɰɢɟɣ ɩɥɚɡɦɵ ɩɪɟɧɟɛɪɟɝɚɟɦ. Ɉɞɧɚɤɨ ɩɪɢ ɛɵɫɬɪɵɯ ɩɪɨɰɟɫɫɚɯ ɷɬɨ ɧɟɞɨɩɭɫɬɢɦɨ. Ȼɨɥɟɟ ɬɨɝɨ, ɨɩɵɬ ɩɨɤɚɡɚɥ, ɱɬɨ ɧɚ ɩɟɪɜɵɯ ɫɬɚɞɢɹɯ ɪɚɡɜɢɬɢɹ

ɢɦɩɭɥɶɫɧɨɝɨ ɪɚɡɪɹɞɚ ɦɨɠɧɨ ɩɪɟɧɟɛɪɟɱɶ ɝɚɡɨɤɢɧɟɬɢɱɟɫɤɢɦ ɞɚɜɥɟɧɢɟɦ ɩɨ ɫɪɚɜɧɟɧɢɸ ɫ ɢɧɟɪɰɢɨɧɧɵɦ ɱɥɟɧɨɦ. ɉɪɢ ɛɵɫɬɪɨɦ ɩɪɨɰɟɫɫɟ ɩɪɨɛɨɣ ɝɚɡɚ ɩɪɨɢɫɯɨɞɢɬ ɩɟɪɜɨɧɚɱɚɥɶɧɨ ɩɨ ɩɟɪɢɮɟɪɢɢ ɪɚɡɪɹɞɧɨɣ ɤɚɦɟɪɵ. ȼ ɮɨɪɦɢɪɨɜɚɧɢɢ ɩɥɚɡɦɟɧɧɨɣ ɨɛɨɥɨɱɤɢ ɫɭɳɟɫɬɜɟɧɧɭɸ ɪɨɥɶ

ɢɝɪɚɸɬ ɷɥɟɦɟɧɬɚɪɧɵɟ ɩɪɨɰɟɫɫɵ − ɢɨɧɢɡɚɰɢɹ, ɪɟɤɨɦɛɢɧɚɰɢɹ ɢ ɩɟɪɟɡɚɪɹɞɤɚ. ɇɚ ɷɬɨɣ ɫɬɚɞɢɢ ɨɛɪɚɡɭɟɬɫɹ ɬɨɧɤɢɣ ɩɪɨɜɨɞɹɳɢɣ ɰɢɥɢɧɞɪ ɩɥɚɡɦɵ. ɉɨ ɦɟɪɟ ɪɚɡɨɝɪɟɜɚ ɢ ɪɨɫɬɚ ɬɨɤɚ ɷɬɚ ɩɥɚɡɦɟɧɧɚɹ ɨɛɨɥɨɱɤɚ ɨɬɪɵɜɚɟɬɫɹ ɨɬ ɫɬɟɧɤɢ ɤɚɦɟɪɵ, ɫɠɢɦɚɟɬɫɹ ɤ ɰɟɧɬɪɭ, ɢɨɧɢɡɭɟɬ ɢ “ɫɝɪɟɛɚɟɬ” ɩɪɢ ɫɠɚɬɢɢ ɧɚɯɨɞɹɳɢɣɫɹ ɜɧɭɬɪɢ ɧɟɟ ɧɟɣɬɪɚɥɶɧɵɣ ɢɥɢ ɫɥɚɛɨ ɢɨɧɢɡɨɜɚɧɧɵɣ ɝɚɡ, ɜɨɜɥɟɤɚɹ ɟɝɨ ɜ ɞɜɢɠɟɧɢɟ ɤ ɰɟɧɬɪɭ. Ɍɚɤɨɣ ɩɪɨɰɟɫɫ ɩɨɥɭɱɢɥ ɧɚɡɜɚɧɢɟ ɞɜɢɠɭɳɟɣɫɹ ɦɚɝɧɢɬɧɨɣ ɫɬɟɧɤɢ (ɜ ɚɧɝɥɢɣɫɤɨɣ ɥɢɬɟɪɚɬɭɪɟ ɫɥɨɠɢɥɫɹ ɬɟɪɦɢɧ snow-plow − ɫɧɟɠɧɵɣ ɩɥɭɝ) ɢ ɬɟɨɪɟɬɢɱɟɫɤɢ ɛɵɥ ɪɚɫɫɦɨɬɪɟɧ ɜ ɋɋɋɊ Ʌɟɨɧɬɨɜɢɱɟɦ ɢ Ɉɫɨɜɰɨɦ [16], ɚ ɜ ɋɒȺ - Ɋɨɡɟɧɛɥɸɬɨɦ. ɉɨɫɥɟ ɫɯɨɠɞɟɧɢɹ ɩɥɚɡɦɟɧɧɨɣ ɨɛɨɥɨɱɤɢ ɤ ɨɫɢ ɜ ɰɟɧɬɪɟ ɤɚɦɟɪɵ ɨɛɪɚɡɭɟɬɫɹ ɰɢɥɢɧɞɪɢɱɟɫɤɢɣ ɩɥɚɡɦɟɧɧɵɣ «ɫɬɨɥɛ», ɫɠɢɦɚɸɳɢɣɫɹ ɩɨɞ ɞɟɣɫɬɜɢɟɦ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɫɨɛɫɬɜɟɧɧɨɝɨ ɬɨɤɚ ɢ, ɜ ɪɟɡɭɥɶɬɚɬɟ, ɛɵɫɬɪɨ ɪɚɡɨɝɪɟɜɚɸɳɢɣɫɹ - ɩɨ ɷɬɨɣ ɩɪɢɱɢɧɟ ɩɪɟɧɟɛɪɟɱɶ ɞɚɜɥɟɧɢɟɦ ɩɥɚɡɦɵ ɭɠɟ ɧɟɥɶɡɹ. ɉɨ ɦɟɪɟ ɪɚɡɨɝɪɟɜɚ ɞɚɜɥɟɧɢɟ ɩɥɚɡɦɵ ɪɚɫɬɟɬ ɢ ɬɨɪɦɨɡɢɬ ɩɪɨɰɟɫɫ ɞɚɥɶɧɟɣɲɟɝɨ ɫɠɚɬɢɹ. ɗɬɚ ɫɬɚɞɢɹ ɡɚɜɟɪɲɚɟɬɫɹ ɨɛɪɚɡɨɜɚɧɢɟɦ ɰɢɥɢɧɞɪɢɱɟɫɤɨɝɨ ɬɨɤɨɜɨɝɨ ɤɚɧɚɥɚ, ɩɨɱɬɢ ɪɚɜɧɨɜɟɫɧɨɝɨ, ɧɨ, ɤɚɤ ɩɨɤɚɡɚɥɢ ɷɤɫɩɟɪɢɦɟɧɬɵ, ɧɟɭɫɬɨɣɱɢɜɨɝɨ, ɜɫɤɨɪɟ ɪɚɡɪɭɲɚɸɳɟɝɨɫɹ, ɝɥɚɜɧɵɦ ɨɛɪɚɡɨɦ, ɡɚ ɫɱɟɬ ɪɚɡɜɢɬɢɹ ɩɟɪɟɬɹɠɟɤ, ɜɟɞɭɳɢɯ ɤ ɨɛɪɵɜɭ ɬɨɤɚ, ɢ ɢɡɝɢɛɨɜ-ɡɦɟɟɤ, ɪɚɡɪɭɲɚɸɳɢɯ ɬɨɤɨɜɵɣ ɤɚɧɚɥ. ɇɚ ɡɚɤɥɸɱɢɬɟɥɶɧɨɣ ɫɬɚɞɢɢ ɪɚɡɪɹɞɚ, ɤɨɝɞɚ ɬɨɤɨɜɵɣ ɤɚɧɚɥ ɪɚɡɪɭɲɚɟɬɫɹ, ɜɨɡɧɢɤɚɸɬ ɷɥɟɤɬɪɨɦɚɝɧɢɬɧɵɟ ɩɨɥɹ, ɩɪɢɜɨɞɹɳɢɟ ɤ ɭɫɤɨɪɟɧɢɸ ɱɚɫɬɢ ɱɚɫɬɢɰ ɩɥɚɡɦɵ, ɜɫɩɥɟɫɤɭ ɪɟɧɬɝɟɧɨɜɫɤɨɝɨ ɢɡɥɭɱɟɧɢɹ ɢ ɧɟɣɬɪɨɧɧɨɦɭ ɢɡɥɭɱɟɧɢɸ, ɟɫɥɢ ɪɚɡɪɹɞ ɩɪɨɢɡɜɨɞɢɬɫɹ ɜ ɞɟɣɬɟɪɢɢ. Ɇɨɳɧɵɣ ɢɦɩɭɥɶɫɧɵɣ ɪɚɡɪɹɞ, ɜ ɤɨɬɨɪɨɦ ɪɟɚɥɢɡɭɟɬɫɹ ɨɩɢɫɚɧɧɚɹ ɜɵɲɟ (ɜɟɫɶɦɚ ɮɪɚɝɦɟɧɬɚɪɧɨ!) ɫɨɜɨɤɭɩɧɨɫɬɶ ɫɨɛɵɬɢɣ, ɩɨɥɭɱɢɥ ɧɚɡɜɚɧɢɟ Z-ɩɢɧɱ, ɝɥɚɜɧɵɦ ɨɛɪɚɡɨɦ ɡɚ ɫɱɟɬ ɝɟɨɦɟɬɪɢɢ ɰɢɥɢɧɞɪɢɱɟɫɤɨɣ ɪɚɡɪɹɞɧɨɣ ɤɚɦɟɪɵ, ɨɫɶ ɤɨɬɨɪɨɣ ɩɪɢɧɹɬɨ ɨɛɵɱɧɨ ɜɵɛɢɪɚɬɶ ɡɚ ɨɫɶ z ɫɢɫɬɟɦɵ ɤɨɨɪɞɢɧɚɬ.

ɇɚ ɮɚɡɟ ɞɜɢɠɟɧɢɹ ɩɥɚɡɦɟɧɧɨɣ ɨɛɨɥɨɱɤɢ ɤ ɨɫɢ, ɫɨɩɪɨɜɨɠɞɚɸɳɟɦɫɹ ɫɝɪɟɛɚɧɢɟɦ ɝɚɡɚ ɢ ɪɨɫɬɨɦ ɦɚɫɫɵ ɩɥɚɡɦɵ, ɪɚɞɢɚɥɶɧɚɹ ɤɨɨɪɞɢɧɚɬɚ ɩɥɚɡɦɟɧɧɨɣ ɨɛɨɥɨɱɤɢ, ɤɨɬɨɪɚɹ ɫɱɢɬɚɟɬɫɹ ɬɨɧɤɨɣ, ɫɨɝɥɚɫɧɨ ɬɟɨɪɢɢ Ʌɟɨɧɬɨɜɢɱɚ − Ɉɫɨɜɰɚ [16], ɨɩɪɟɞɟɥɹɟɬɫɹ ɭɪɚɜɧɟɧɢɟɦ:

d §

dr ·

1

&

&

Bϕ2

¨m

¸

=

( j

× B )r 2πr

≡ −

2πr ,

(3.21)

c

8π

dt ©

dt ¹

ɝɞɟ m - ɦɚɫɫɚ ɟɞɢɧɢɰɵ ɞɥɢɧɵ ɲɧɭɪɚ ɩɥɚɡɦɵ

m = m (1 −

r2

), m = πρa2

,

a2

0

0

ɝɞɟ ɚ - ɧɚɱɚɥɶɧɵɣ ɪɚɞɢɭɫ ɨɛɨɥɨɱɤɢ, m0 - ɧɚɱɚɥɶɧɚɹ ɦɚɫɫɚ ɝɚɡɚ ɜ ɪɚɡɪɹɞɧɨɣ ɤɚɦɟɪɟ ɧɚ ɟɞɢɧɢɰɭ ɞɥɢɧɵ ɜɞɨɥɶ ɨɫɢ;

2I( t ) Bϕ = cr

ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ ɬɨɤɚ ɫɧɚɪɭɠɢ ɨɬ ɩɥɚɡɦɟɧɧɨɣ ɨɛɨɥɨɱɤɢ. ȼɧɭɬɪɢ ɨɛɨɥɨɱɤɢ ɩɪɢ

ɰɢɥɢɧɞɪɢɱɟɫɤɨɣ ɫɢɦɦɟɬɪɢɢ ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ, ɨɱɟɜɢɞɧɨ, ɪɚɜɧɨ ɧɭɥɸ. ɉɨ ɷɬɨɣ ɩɪɢɱɢɧɟ ɜ ɩɪɚɜɨɣ ɱɚɫɬɢ ɭɪɚɜɧɟɧɢɹ (3.21), ɩɪɟɞɫɬɚɜɥɹɸɳɟɣ ɫɨɛɨɣ ɪɚɞɢɚɥɶɧɭɸ ɫɢɥɭ, ɞɟɣɫɬɜɭɸɳɭɸ ɧɚ

ɨɛɨɥɨɱɤɭ ɜ ɪɚɫɱɟɬɟ ɧɚ ɟɞɢɧɢɰɭ ɟɟ ɞɥɢɧɵ ɜɞɨɥɶ ɨɫɢ, ɡɧɚɤ ɨɛɹɡɚɬɟɥɶɧɨ ɞɨɥɠɟɧ ɛɵɬɶ ɨɬɪɢɰɚɬɟɥɶɧɵɦ! ɂɧɨɝɞɚ ɜ ɥɟɜɭɸ ɱɚɫɬɶ (3.21) ɜɜɨɞɹɬ ɞɨɩɨɥɧɢɬɟɥɶɧɵɣ ɤɨɷɮɮɢɰɢɟɧɬ k, ɭɱɢɬɵɜɚɸɳɢɣ ɞɨɥɸ ɡɚɯɜɚɬɵɜɚɟɦɨɣ ɦɚɫɫɵ ɢ ɪɚɜɧɵɣ ɟɞɢɧɢɰɟ ɩɪɢ ɩɨɥɧɨɦ ɫɝɪɟɛɚɧɢɢ.

Ⱦɥɹ ɨɩɪɟɞɟɥɟɧɢɹ ɜɟɥɢɱɢɧɵ ɪɚɡɪɹɞɧɨɝɨ ɬɨɤɚ I(t) ɧɟɨɛɯɨɞɢɦɨ ɞɨɩɨɥɧɢɬɟɥɶɧɨɟ ɭɪɚɜɧɟɧɢɟ - ɷɥɟɤɬɪɨɬɟɯɧɢɱɟɫɤɨɟ ɭɪɚɜɧɟɧɢɟ ɰɟɩɢ ɞɥɹ ɪɚɡɪɹɞɧɨɝɨ ɤɨɧɬɭɪɚ. ɗɬɨ, ɤɨɧɟɱɧɨ, ɭɫɥɨɠɧɹɟɬ ɪɟɲɟɧɢɟ. ɇɨ ɧɚ ɧɚɱɚɥɶɧɨɣ ɫɬɚɞɢɢ ɦɨɠɧɨ ɩɨɥɚɝɚɬɶ, ɱɬɨ ɬɨɤ ɪɚɫɬɟɬ ɥɢɧɟɣɧɨ ɩɨ ɜɪɟɦɟɧɢ, ɬɚɤ ɱɬɨ

I( t ) = I0t ,

ɝɞɟ I0 - ɬɟɦɩ ɧɚɪɚɫɬɚɧɢɹ ɬɨɤɚ (ɡɞɟɫɶ ɩɨɫɬɨɹɧɧɚɹ ɜɟɥɢɱɢɧɚ), ɨɩɪɟɞɟɥɹɟɦɵɣ

ɷɥɟɤɬɪɨɬɟɯɧɢɱɟɫɤɢɦɢ ɩɚɪɚɦɟɬɪɚ ɪɚɡɪɹɞɧɨɣ ɰɟɩɢ.

Ɋɟɲɟɧɢɟ ɭɪɚɜɧɟɧɢɹ (3.21) ɞɥɹ ɥɢɧɟɣɧɨ ɧɚɪɚɫɬɚɸɳɟɝɨ ɬɨɤɚ ɞɚɧɨ ɜ [12]. Ɉɧɨ ɩɪɟɞɫɤɚɡɵɜɚɟɬ, ɱɬɨ ɜ ɨɩɪɟɞɟɥɟɧɧɵɣ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ

t = t	ɨɫɨɛ	= 1.5( ac / I	)1/ 2 m1/ 4	,	(3.22)
		0	0

ɧɚɡɵɜɚɟɦɵɣ ɦɨɦɟɧɬɨɦ ɨɫɨɛɟɧɧɨɫɬɢ, ɩɥɚɡɦɟɧɧɚɹ ɨɛɨɥɨɱɤɚ ɫɯɥɨɩɵɜɚɟɬɫɹ ɧɚ ɨɫɢ ɫɢɫɬɟɦɵ. Ɇɨɦɟɧɬ ɨɫɨɛɟɧɧɨɫɬɢ ɪɟɚɥɶɧɨ ɧɚɛɥɸɞɚɟɬɫɹ ɧɚ ɷɤɫɩɟɪɢɦɟɧɬɟ (ɧɨ, ɤɨɧɟɱɧɨ, ɫɠɚɬɢɹ ɞɨ ɧɭɥɟɜɨɝɨ ɪɚɞɢɭɫɚ ɧɟ ɩɪɨɢɫɯɨɞɢɬ), ɩɪɢɱɟɦ ɩɪɟɞɫɤɚɡɚɧɢɹ ɫ ɩɨɦɨɳɶɸ (3.22) ɭɞɢɜɢɬɟɥɶɧɨ ɬɨɱɧɨ ɫɨɨɬɜɟɬɫɬɜɭɸɬ ɧɚɛɥɸɞɟɧɢɹɦ (ɩɨɞɪɨɛɧɟɟ ɫɦ. [12], ɬɢɩɢɱɧɵɟ ɡɧɚɱɟɧɢɹ tɨɫɨɛ ɫɨɫɬɚɜɥɹɸɬ 2 - 10 ɦɤɫ). Ɂɚɦɟɬɢɦ, ɱɬɨ ɜɟɥɢɱɢɧɚ tɨɫɨɛ ɨɩɪɟɞɟɥɹɟɬɫɹ, ɮɚɤɬɢɱɟɫɤɢ, ɬɨɥɶɤɨ ɧɚɱɚɥɶɧɵɦɢ ɡɧɚɱɟɧɢɹɦɢ ɜɟɥɢɱɢɧ.

Ɋɢɫ. 3.3. Ɋɚɡɧɨɜɢɞɧɨɫɬɢ ɰɢɥɢɧɞɪɢɱɟɫɤɨɝɨ (ɚ,ɛ) ɢ ɧɟɰɢɥɢɧɞɪɢɱɟɫɤɨɝɨ (ɜ,ɝ) Z-ɩɢɧɱɚ: ɚ − ɤɥɚɫɫɢɱɟɫɤɢɣ Z-ɩɢɧɱ, ɛ − ɦɢɤɪɨɩɢɧɱ, ɜ − ɩɥɚɡɦɟɧɧɵɣ ɮɨɤɭɫ Ɏɢɥɢɩɩɨɜɚ, ɝ − ɩɭɲɤɚ Ɇɟɣɡɟɪɚ. Ɋ −ɪɚɡɪɹɞɧɢɤ, ɋ − ɛɚɬɚɪɟɹ ɤɨɧɞɟɧɫɚɬɨɪɨɜ, ɫɬɪɟɥɤɚ − ɧɚɩɪɚɜɥɟɧɢɟ ɬɨɤɚ

ȼ ɧɚɫɬɨɹɳɟɟ ɜɪɟɦɹ ɢɡɭɱɟɧɨ ɷɤɫɩɟɪɢɦɟɧɬɚɥɶɧɨ ɰɟɥɨɟ ɫɟɦɟɣɫɬɜɨ ɪɚɡɥɢɱɧɵɯ ɦɨɞɢɮɢɤɚɰɢɣ Z-ɩɢɧɱɚ, ɧɟɤɨɬɨɪɵɟ ɢɡ ɩɪɟɞɫɬɚɜɢɬɟɥɟɣ ɤɨɬɨɪɨɝɨ ɫɯɟɦɚɬɢɱɧɨ ɩɨɤɚɡɚɧɵ ɧɚ ɪɢɫ. 3.3. Ɇɧɨɝɨɨɛɪɚɡɢɟ ɦɨɞɢɮɢɤɚɰɢɣ ɪɚɡɪɹɞɧɵɯ ɭɫɬɪɨɣɫɬɜ ɬɚɤɨɝɨ ɬɢɩɚ ɧɟ ɫɥɭɱɚɣɧɨ: ɩɨ ɫɭɬɢ ɞɟɥɚ, ɜɫɹ ɢɫɬɨɪɢɹ ɢɫɫɥɟɞɨɜɚɧɢɣ ɜ ɨɛɥɚɫɬɢ ɭɩɪɚɜɥɹɟɦɨɝɨ ɬɟɪɦɨɹɞɟɪɧɨɝɨ ɫɢɧɬɟɡɚ ɛɟɪɟɬ ɧɚɱɚɥɨ ɨɬ ɦɨɳɧɵɯ ɢɦɩɭɥɶɫɧɵɯ ɪɚɡɪɹɞɨɜ ɜ ɝɚɡɟ, ɜ ɤɨɬɨɪɵɯ ɜɩɟɪɜɵɟ ɛɵɥɢ ɨɛɧɚɪɭɠɟɧɵ «ɬɟɪɦɨɹɞɟɪɧɵɟ» ɧɟɣɬɪɨɧɵ ɢ ɤɨɬɨɪɵɟ ɞɥɢɬɟɥɶɧɨɟ ɜɪɟɦɹ ɛɵɥɢ ɪɟɤɨɪɞɫɦɟɧɚɦɢ ɩɨ ɩɚɪɚɦɟɬɪɭ nτ - ɩɪɨɢɡɜɟɞɟɧɢɸ ɤɨɧɰɟɧɬɪɚɰɢɢ ɩɥɚɡɦɵ ɧɚ ɜɪɟɦɹ ɭɞɟɪɠɚɧɢɹ. Ɇɧɨɝɢɟ ɫɜɨɢ ɩɨɡɢɰɢɢ ɜɜɢɞɭ ɰɟɥɨɝɨ ɪɹɞɚ ɭɧɢɤɚɥɶɧɵɯ ɫɜɨɣɫɬɜ ɩɢɧɱɢ ɧɟ ɭɬɪɚɬɢɥɢ ɞɨ ɫɢɯ ɩɨɪ.

§ 26. ȼɡɚɢɦɧɨɟ ɩɪɨɧɢɤɧɨɜɟɧɢɟ ɩɥɚɡɦɵ ɢ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ

Ɇɚɝɧɢɬɧɨɟ ɞɚɜɥɟɧɢɟ ɞɟɣɫɬɜɭɟɬ ɧɚ ɩɪɨɜɨɞɧɢɤ ɜ ɧɚɩɪɚɜɥɟɧɢɢ ɩɟɪɩɟɧɞɢɤɭɥɹɪɧɨɦ ɤ ɦɚɝɧɢɬɧɵɦ ɫɢɥɨɜɵɦ ɥɢɧɢɹɦ, ɜ ɬɟɱɟɧɢɟ ɜɪɟɦɟɧɢ, ɦɟɧɶɲɟɦ ɫɤɢɧɨɜɨɝɨ ɜɪɟɦɟɧɢ t<τs. Ɂɚ ɜɪɟɦɹ, ɛɨɥɶɲɟɟ ɫɤɢɧɨɜɨɝɨ t>τs, ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ ɭɫɩɟɜɚɟɬ “ɩɪɨɫɨɱɢɬɶɫɹ” ɜ ɩɪɨɜɨɞɧɢɤ ɢ ɜɟɥɢɱɢɧɵ ɢɧɞɭɤɰɢɢ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɜɧɭɬɪɢ ɢ ɜɧɟ ɩɪɨɜɨɞɧɢɤɚ ɜɵɪɚɜɧɢɜɚɸɬɫɹ. ȼ ɫɥɭɱɚɟ, ɤɨɝɞɚ ɪɚɫɫɦɚɬɪɢɜɚɟɬɫɹ ɩɪɨɧɢɤɧɨɜɟɧɢɟ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ ɜ ɩɥɚɡɦɭ, ɧɭɠɧɨ ɭɱɢɬɵɜɚɬɶ, ɱɬɨ ɩɪɨɰɟɫɫ ɩɪɨɧɢɤɧɨɜɟɧɢɹ ɜɡɚɢɦɧɵɣ − ɧɟ ɬɨɥɶɤɨ ɩɨɥɟ ɩɪɨɧɢɤɚɟɬ ɜ ɩɥɚɡɦɭ, ɧɨ ɢ ɩɥɚɡɦɚ ɩɪɨɧɢɤɚɟɬ ɜ ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ, ɧɚɩɪɢɦɟɪ, ɡɚ ɫɱɟɬ ɞɢɮɮɭɡɢɢ, ɢɦɟɸɳɟɣ ɦɟɫɬɨ ɢ ɜ ɫɥɭɱɚɟ, ɤɨɝɞɚ ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ ɨɞɧɨɪɨɞɧɨ.

ɉɪɨɧɢɤɧɨɜɟɧɢɟ ɩɨɥɹ ɜ ɩɪɨɜɨɞɧɢɤ ɫ ɩɨɫɬɨɹɧɧɨɣ ɩɪɨɜɨɞɢɦɨɫɬɶɸ σ, ɢɥɢ, ɱɬɨ ɬɨ ɠɟ ɫɚɦɨɟ, ɜ ɨɞɧɨɪɨɞɧɭɸ ɧɟɩɨɞɜɢɠɧɭɸ ɩɥɚɡɦɭ ɫ ɩɨɫɬɨɹɧɧɨɣ ɬɟɦɩɟɪɚɬɭɪɨɣ, ɮɨɪɦɚɥɶɧɨ ɚɧɚɥɨɝɢɱɧɨ ɞɢɮɮɭɡɢɢ, ɬɚɤ ɤɚɤ ɨɩɢɫɵɜɚɟɬɫɹ (ɩɪɢɛɥɢɠɟɧɧɨ) ɫɯɨɞɧɵɦ ɭɪɚɜɧɟɧɢɟɦ:

	∂	B& = Dɦɚɝ∆B&,	(3.23)
	∂t

ɫ ɤɨɷɮɮɢɰɢɟɧɬ ɦɚɝɧɢɬɧɨɣ ɞɢɮɮɭɡɢɢ Dɦɚɝ, ɨɩɪɟɞɟɥɹɟɦɵɦ ɮɨɪɦɭɥɨɣ (3.2). ɏɨɪɨɲɨ ɢɡɜɟɫɬɧɨ, ɱɬɨ ɷɬɨ ɭɪɚɜɧɟɧɢɟ ɨɩɢɫɵɜɚɟɬ ɨɛɵɱɧɵɣ ɫɤɢɧ-ɷɮɮɟɤɬ.

Ƚɥɭɛɢɧɚ ɩɪɨɧɢɤɧɨɜɟɧɢɹ ɩɨɥɹ lm ɪɚɫɬɟɬ ɫɨ ɜɪɟɦɟɧɟɦ ɩɨ ɡɚɤɨɧɭ lm ~ Dɦɚɝt .

ȼ ɩɪɨɬɢɜɨɩɨɥɨɠɧɨɦ ɫɥɭɱɚɟ, ɤɨɝɞɚ ɩɥɚɡɦɚ ɩɨɦɟɳɟɧɚ ɜ ɩɨɫɬɨɹɧɧɨɟ ɨɞɧɨɪɨɞɧɨɟ ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ, ɟɟ ɝɪɚɧɢɰɚ ɩɨɫɬɟɩɟɧɧɨ ɪɚɡɦɵɜɚɟɬɫɹ ɢ ɷɬɨ ɪɚɡɦɵɬɢɟ ɝɪɚɧɢɰɵ ɩɥɚɡɦɵ ɫɜɹɡɚɧɨ ɫ ɞɜɢɠɟɧɢɟɦ ɱɚɫɬɢɰ ɩɨɩɟɪɟɤ ɩɨɥɹ. Ⱥ ɷɬɨ ɜɨɡɦɨɠɧɨ ɬɨɥɶɤɨ ɩɪɢ ɫɬɨɥɤɧɨɜɟɧɢɢ ɱɚɫɬɢɰ, ɬ.ɟ. ɜ ɩɪɨɰɟɫɫɟ ɩɨɩɟɪɟɱɧɨɣ ɞɢɮɮɭɡɢɢ. ɗɬɨɬ ɩɪɨɰɟɫɫ ɨɩɢɫɵɜɚɟɬɫɹ ɭɪɚɜɧɟɧɢɟɦ

		∂	n = div( D n ) ,			(3.24)
		∂t
	ɝɞɟ			< ρ	>2
	D =			e	.	(3.25)
				τei

ȼɟɥɢɱɢɧɚ ɪɚɡɦɵɬɢɹ ɝɪɚɧɢɰɵ ɩɥɚɡɦɵ lp ɡɚ ɜɪɟɦɹ t ɨɩɪɟɞɟɥɹɟɬɫɹ ɬɟɩɟɪɶ ɜɵɪɚɠɟɧɢɟɦ:

lp ~ D t .

Ʌɸɛɨɩɵɬɧɨ ɨɬɦɟɬɢɬɶ, ɱɬɨ ɮɨɪɦɚɥɶɧɨ ɢɦɟɟɬ ɦɟɫɬɨ ɫɨɨɬɧɨɲɟɧɢɟ [17]

D	=	1	βD		,	(3.26)
		2
				ɦɚɝ

ɢ, ɫɥɟɞɨɜɚɬɟɥɶɧɨ, ɡɚ ɬɨɠɟ ɫɚɦɨɟ ɜɪɟɦɹ ɬɨɥɳɢɧɚ ɫɥɨɹ ɩɪɨɧɢɤɧɨɜɟɧɢɹ ɩɥɚɡɦɵ ɧɢɡɤɨɝɨ ɞɚɜɥɟɧɢɹ ɫ β<1 ɜ ɨɞɧɨɪɨɞɧɨɟ ɩɨɥɟ ɨɤɚɡɵɜɚɟɬɫɹ ɜ β / 2 ɪɚɡ ɦɟɧɶɲɟ

ɬɨɥɳɢɧɵ ɫɥɨɹ ɩɪɨɧɢɤɧɨɜɟɧɢɹ ɩɨɥɹ ɜ ɨɞɧɨɪɨɞɧɭɸ ɧɟɩɨɞɜɢɠɧɭɸ ɩɥɚɡɦɭ. ȼɚɠɧɨ ɜɵɹɫɧɢɬɶ, ɤɚɤɨɣ ɩɪɨɰɟɫɫ ɹɜɥɹɟɬɫɹ ɞɨɦɢɧɢɪɭɸɳɢɦ, ɤɨɝɞɚ ɢɦɟɟɬ

ɦɟɫɬɨ ɜɡɚɢɦɧɚɹ ɞɢɮɮɭɡɢɹ ɩɥɚɡɦɵ ɢ ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ, ɬ.ɟ. ɜ ɫɥɭɱɚɟ, ɤɨɝɞɚ ɢ ɩɥɚɡɦɚ ɢ ɩɨɥɟ ɹɜɥɹɸɬɫɹ ɧɟɨɞɧɨɪɨɞɧɵɦɢ. ȼ ɨɛɳɟɦ ɜɢɞɟ ɷɬɨ ɫɥɨɠɧɚɹ ɡɚɞɚɱɚ, ɧɨ ɞɨɫɬɚɬɨɱɧɨ ɩɪɨɫɬɨɟ ɟɟ ɪɟɲɟɧɢɟ ɦɨɠɧɨ ɩɨɥɭɱɢɬɶ, ɟɫɥɢ ɨɝɪɚɧɢɱɢɬɶɫɹ ɫɥɭɱɚɟɦ ɩɥɚɡɦɵ ɧɢɡɤɨɝɨ ɞɚɜɥɟɧɢɹ. ɉɪɨɰɟɫɫ ɞɢɮɮɭɡɢɢ ɹɜɥɹɟɬɫɹ ɧɟɫɬɚɰɢɨɧɚɪɧɵɦ, ɧɨ ɨɛɵɱɧɨ ɟɝɨ ɦɨɠɧɨ ɫɱɢɬɚɬɶ ɦɟɞɥɟɧɧɵɦ ɧɚ ɦɚɫɲɬɚɛɚɯ ɜɪɟɦɟɧ ɭɫɬɚɧɨɜɥɟɧɢɹ

ɪɚɜɧɨɜɟɫɢɹ ɩɥɚɡɦɵ. ɂɧɵɦɢ ɫɥɨɜɚɦɢ, ɨɩɢɫɵɜɚɹ ɞɢɮɮɭɡɢɸ, ɜ ɭɪɚɜɧɟɧɢɢ ɞɜɢɠɟɧɢɹ (3.11) ɦɨɠɧɨ ɩɪɟɧɟɛɪɟɱɶ ɢɧɟɪɰɢɟɣ, ɢ ɩɪɢɧɹɬɶ, ɱɬɨ

1 &

&

j

× B − p ≈ 0 .

(3.27)

c

ɋɱɢɬɚɹ ɷɬɨ ɭɫɥɨɜɢɟ ɜɵɩɨɥɧɟɧɧɵɦ, ɢɡ ɡɚɤɨɧɚ Ɉɦɚ (3.8) ɩɨɥɭɱɢɦ ɜɟɥɢɱɢɧɭ

ɧɚɩɪɹɠɟɧɧɨɫɬɢ ɷɥɟɤɬɪɢɱɟɫɤɨɝɨ ɩɨɥɹ

&

&j

1 &

&

1

p .

E =

−

v

× B +

(3.28)

σ

c

2n|e|

ɋɬɪɟɦɹɫɶ ɦɚɤɫɢɦɚɥɶɧɨ ɭɩɪɨɫɬɢɬɶ ɨɩɢɫɚɧɢɟ, ɨɝɪɚɧɢɱɢɦɫɹ ɫɥɭɱɚɟɦ ɞɢɮɮɭɡɢɢ ɩɥɚɡɦɵ ɫ ɩɨɫɬɨɹɧɧɨɣ ɬɟɦɩɟɪɚɬɭɪɨɣ Ɍ=const ɜ ɧɟɨɞɧɨɪɨɞɧɨɦ ɦɚɝɧɢɬɧɨɦ ɩɨɥɟ ɫ ɩɪɹɦɵɦɢ ɫɢɥɨɜɵɦɢ ɥɢɧɢɹɦɢ, ɨɪɢɟɧɬɢɪɨɜɚɧɧɵɦɢ ɜɞɨɥɶ ɨɫɢ z ɫɢɫɬɟɦɵ

ɤɨɨɪɞɢɧɚɬ. ɋɱɢɬɚɟɦ, ɱɬɨ ɜɞɨɥɶ ɷɬɨɝɨ ɧɚɩɪɚɜɥɟɧɢɹ ɩɨɥɟ ɢ ɩɥɚɡɦɚ ɨɞɧɨɪɨɞɧɵ. ȼ
ɷɬɢɯ ɭɫɥɨɜɢɹɯ ɩɨɞɫɬɚɧɨɜɤɚ ɩɨɥɹ E&			ɢɡ (3.28) ɜ ɡɚɤɨɧ ɢɧɞɭɤɰɢɢ
&	1 ∂ B&
rot E = −		∂ t ,
	c

ɫ ɩɨɫɥɟɞɭɸɳɢɦ ɢɫɩɨɥɶɡɨɜɚɧɢɟɦ ɭɪɚɜɧɟɧɢɹ ɧɟɩɪɟɪɵɜɧɨɫɬɢ (3.4), ɤɨɬɨɪɨɟ ɡɞɟɫɶ ɭɞɨɛɧɨ ɡɚɩɢɫɚɬɶ ɜ ɜɢɞɟ

1 dn = −div v&, n dt

ɩɪɢɜɨɞɢɬ ɤ ɫɨɨɬɧɨɲɟɧɢɸ

d §		B ·			∆B
	¨	z	¸	= D	z .
dt ©		n ¹			ɦɚɝ n

ɍɱɬɟɦ ɞɚɥɟɟ, ɱɬɨ (3.27) ɷɤɜɢɜɚɥɟɧɬɧɨ ɫɥɟɞɭɸɳɟɦɭ ɭɫɥɨɜɢɸ

1 &		&	Bz	2
	j	× B − p = − (			+ p )
c			8π

Ɉɧɨ ɨɡɧɚɱɚɟɬ, ɱɬɨ ɫɭɦɦɚɪɧɨɟ ɩɨɞɞɟɪɠɢɜɚɟɬɫɹ ɩɨɫɬɨɹɧɧɵɦ:

Bz 2 + p = B0 2 ,

8π 8π

≈ 0 .

ɞɚɜɥɟɧɢɟ ɩɥɚɡɦɵ ɢ

(3.29)

(3.30)

ɦɚɝɧɢɬɧɨɝɨ ɩɨɥɹ

(3.31)

ɝɞɟ ȼ0 ɫɱɢɬɚɟɬɫɹ ɡɚɞɚɧɧɨɣ ɜɟɥɢɱɢɧɨɣ. Ɂɚɦɟɬɢɦ, ɱɬɨ ɩɪɢ ɜɵɜɨɞɟ (3.29) − (3.31) ɹɜɧɨ ɧɢɤɚɤ ɧɟ ɢɫɩɨɥɶɡɨɜɚɥɚɫɶ ɩɪɟɞɩɨɥɚɝɚɟɦɚɹ ɦɚɥɨɫɬɶ ɜɟɥɢɱɢɧɵ β, ɬɚɤ ɱɬɨ ɜ ɷɬɨɦ ɩɥɚɧɟ ɨɧɢ ɹɜɥɹɸɬɫɹ ɩɨɤɚ ɬɨɱɧɵɦɢ. ɍɱɬɟɦ ɷɬɭ ɦɚɥɨɫɬɶ, ɬɨɝɞɚ, ɜɜɟɞɹ ɞɥɹ ɭɞɨɛɫɬɜɚ ɩɪɨɦɟɠɭɬɨɱɧɨɟ ɨɛɨɡɧɚɱɟɧɢɟ,

8πp

β0 = B0 2 << 1 ,

ɢɡ (3.30) ɩɪɢɛɥɢɠɟɧɧɨ ɩɨɥɭɱɚɟɦ ɜɟɥɢɱɢɧɭ ɦɚɝɧɢɬɧɨɣ ɢɧɞɭɤɰɢɢ

	B	B (1 −	1	β ).	(3.32)
			2
	z	0		0

ɉɨɫɤɨɥɶɤɭ ɜɟɥɢɱɢɧɚ β0 ɡɞɟɫɶ ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɚ ɤɨɧɰɟɧɬɪɚɰɢɢ ɩɥɚɡɦɵ, ɬɨ, ɢɫɩɨɥɶɡɭɹ ɷɬɨ ɫɨɨɬɧɨɲɟɧɢɟ, ɦɨɠɧɨ ɩɨɤɚɡɚɬɶ (ɩɪɟɞɥɚɝɚɟɦ ɱɢɬɚɬɟɥɸ ɜ ɤɚɱɟɫɬɜɟ

ɭɩɪɚɠɧɟɧɢɹ ɩɪɨɞɟɥɚɬɶ ɷɬɨɬ ɧɟɫɥɨɠɧɵɣ ɜɵɜɨɞ ɫɚɦɨɫɬɨɹɬɟɥɶɧɨ), ɱɬɨ ɭɪɚɜɧɟɧɢɹ (3.29), (3.30) ɫɜɨɞɹɬɫɹ ɤ ɨɞɧɨɦɭ

∂	n = div(	1	β D		n ),	(3.33)
∂t		2
			0	ɦɚɝ

ɮɨɪɦɚɥɶɧɨ ɫɨɜɩɚɞɚɸɳɟɦɭ ɫ ɭɪɚɜɧɟɧɢɟɦ ɞɢɮɮɭɡɢɢ ɩɥɚɡɦɵ ɜ ɨɞɧɨɪɨɞɧɨɦ ɩɨɥɟ (3.24). Ɍɟɩɟɪɶ, ɨɞɧɚɤɨ, ɜ ɫɢɥɭ (3.32), ɦɚɝɧɢɬɧɨɟ ɩɨɥɟ ɨɞɧɨɡɧɚɱɧɨ ɫɜɹɡɚɧɨ ɫ