Задание по эконометрике / Задача для КР

Задание № 1

1.Построить поле корреляции, сформулировать гипотезу о форме связи

ипостроить эмпирическую линию регрессии (линию тренда).

Рассмотрим пример использования данных функций. Исходные данные, в которых содержатся цена и спрос на некоторый товар, представлены в таблице 1.

Таблица № 1

Номер наблюдения	Цена	Спрос
	x (р.)	y (тыс.шт.)
1	15,09р.	125,1779
2	15,21р.	123,8094
3	15,28р.	121,175
4	15,49р.	116,9143
5	15,54р.	119,8643
6	15,62р.	118,0681
7	15,70р.	123,5887
8	15,91р.	117,0877
9	15,92р.	116,1699
10	15,95р.	118,3436
11	16,31р.	116,2008
12	16,33р.	111,4565
13	16,60р.	115,1026
14	16,69р.	110,1056
15	16,76р.	110,0231

С помощью возможностей программного комплекса Exсel построим поле корреляции. Для этого необходимо задать точечную диаграмму (диаграмма обязательно должна быть точечной), и выбрав произвольную точку в контекстном меню, можно выбрать пункт Добавить линию тренда. Хотя термин «тренд» имеет несколько другой смысл, применительно к временным рядам, в данном случае термины «тренд» и «линия регрессии» будем отождествлять друг с другом. Выбор пункта Добавить линию тренда приведет к появлению диалогового окна, у которого имеются две закладки — Тип и Параметры (рис. 1).

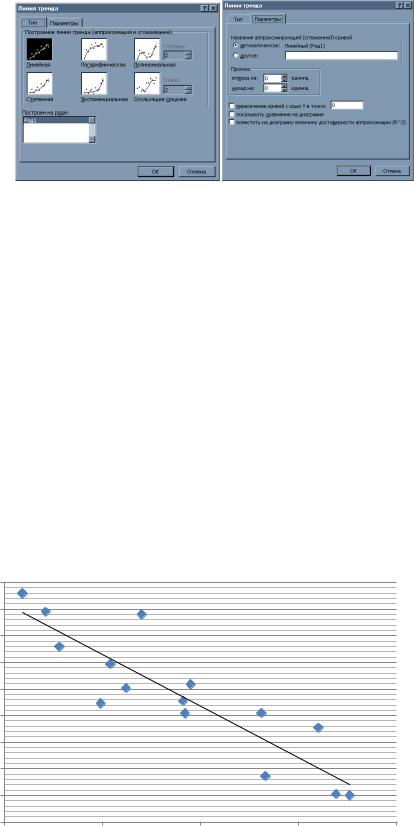
Рис. 1

На закладке Тип необходимо выбрать один из возможных видов уравнения регрессии. Если на диаграмме имеется несколько рядов точек, то линию регрессии можно построить для любой, задав значение соответствующего параметра —

Построить на ряде.

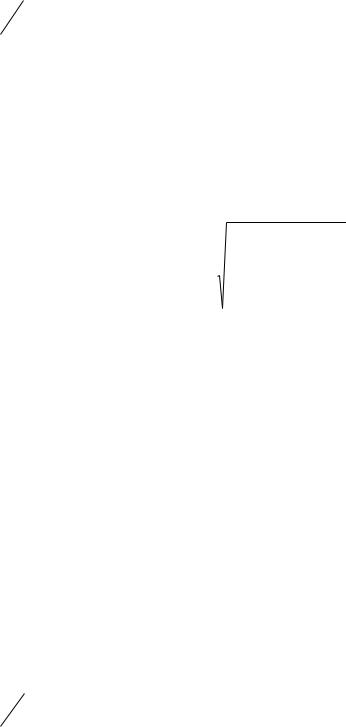
На закладке Параметры можно задать дополнительную информацию, которая будет присутствовать на диаграмме. Во-первых, это возможность прогнозирования, что позволит построить линии тренда вперед или назад на соответствующее число единиц. Опция Показывать уравнение на диаграмме позволяет выдавать вид уравнения, а опция Поместить на диаграмму величину достоверности аппроксимации (R2) выводит значение коэффициента детерминации. Построив точечную диаграммы для данных, заданных в таблице 1, и линию тренда, можно получить диаграмму, которая изображена на рисунке 2.

126,00
124,00
122,00
120,00
118,00
116,00
114,00
112,00		y = -7,7032x + 239,97
110,00		R² = 0,7858
108,00
15,00	15,50	16,00	16,50	17,00
		Рис. 2
В данном случае можно сформулировать гипотезу о наличии связи между
ценой и спросом на товар, носящей скорее всего линейный характер.

2. Построить уравнение регрессии зависимости У от X рассчитать

параметры линейной, степенной, показательной функции и выбрать оптимальную модель (провести оценку моделей через среднюю ошибку аппроксимации (А) и F- критерий Фишера.

2.1Линейная модель

Вмодели парной линейной регрессии зависимость между переменными в генеральной совокупности представляется в виде:

yi 0 1 xi i

(1.1)

где yi — зависимые переменные, xi — независимые переменные;

β0, β1 — параметры уравнения регрессии, подлежащие оцениванию;i — случайная ошибка модели регрессии

На основании выборочного наблюдения оценивается выборочное уравнение регрессии (линия регрессии):

yi 0 1 xi

(1.2)

Неизвестные значения ( 0 , 1 ) определяются методом наименьших

квадратов (МНК), вычисление которых сводиться к разрешение системы уравнений:

~

n

2

~

n

n

1

xi

0

xi xi yi

i 1

i 1

i 1

(1.3)

~

n

~

n

1

xi

0

n yi

i 1

i 1

Решением системы нормальных уравнений являются оценки неизвестных

параметров уравнения регрессии β0

и β1:

n

n

n

n xi yi

xi yi

~

xy x y

n 2

n

2

,

(1.4)

1

x2 x 2

i 1

i 1

i 1

n xi

xi

i 1

i 1

~

~

0

y 1 x

(1.5)

где y — среднее значение зависимого признака; x — среднее значение независимого признака;

xy — среднее арифметическое значение произведения зависимого и независимого признаков.

Для удобства расчетов сделаем промежуточные расчеты и внесем их в таблицу вида:

Вспомогательная таблица расчетов

Год	x	y	x	2	xy	2	~	…
						y	yi
1	15,09	125,18	227,71		1888,93	15669,51	123,73	…
2	15,21	123,81	231,34		1883,14	15328,77	122,81	…
…	…	…	…		…	…	…	…
15	16,76	110,02	280,90		1843,99	12105,08	110,87	…
Итого:	238,40	1763,09	3793,11		27989,43	207 544,60	1 763,15	…

Подставив данные из таблицы в формулы 1.4, 1.5 и произведя расчеты получим линейную модель зависимости y от x имеет вид:

yi 239,97 7,703 xi

3. Для определения силы взаимосвязи линейны коэффициент парной

корреляции.

Коэффициентом корреляции (r) характеризует тесноту связи и рассчитывается по формуле:

xy x y

r (1.6)

xy	Sx S y

Sy — выборочное среднеквадратическое отклонение зависимой переменной y. Этот показатель характеризует, на сколько единиц в среднем отклоняются значения зависимого признака y от его среднего значения. Он вычисляется по формуле:

Sy y2 y2

Коэффициент корреляции лежит в пределах -1< r <1. В случае если r=0, связи нет. Если r 1, то между двумя величинами существует сильная функциональная

связь. При положительном r наблюдается прямая связь, т.е. с увеличением независимой переменной - x увеличивается зависимая - y. При отрицательном коэффициенте существует обратная связь, с увеличением независимой переменной зависимая переменная уменьшается. Связь считается сильной при r 0,70 , средней

при 0,50

r

0,69 ,

умеренной при 0,30

r

0,49 , слабой

при 0,20

r

0,29 , очень

слабой при

r

0,19

Рассчитаем линейный коэффициент парной корреляции:

rxy

1865,96 15,89 117,54

0,884

13836,31 117,542 252,87 15,892

Что свидетельствует о сильной обратной связи.

Для оценки качества построенного уравнения рассчитаем коэффициент детерминации и среднюю ошибку аппроксимации.

Коэффициент детерминации указывает, какой процент вариации функции Y объясняется воздействием фактора Х. Коэффициент детерминации изменяется от 0 до 1, и чем ближе значение данного коэффициента к 1, тем удачнее выбранная форма регрессионной зависимости аппроксимирует данные. В разобранном примере для линейной модели коэффициент детерминации равен:

rxy2 ( 0,884)2 0,781

Вариация результата на 78,1 % объясняется вариацией фактора Х

Показатель средней ошибки аппроксимации рассчитывается по формуле:

			n			~
		1			yi	yi
Ay								100%
						yi
		n i 1

Максимально допустимым значением данного показателя считается 12—15%. Если средняя ошибка аппроксимации составляет менее 6—7%, то качество модели считается хорошим.

Величина средней ошибки аппроксимации А составляет 1,4 %, что свидетельствует о высоком качестве модели.

Проверка значимость полученных с помощью метода наименьших квадратов оценок коэффициентов регрессии, значимость парного линейного коэффициента корреляции и уравнения регрессии в целом с помощью статистических гипотез.

При проверке значимости (предположения того, что параметры отличаются от нуля) коэффициентов регрессии выдвигается основная гипотеза H0 о незначимости полученных оценок, например:

Н0 1 0

вкачестве альтернативной (или обратной) выдвигается гипотеза о значимости

коэффициентов регрессии, например:

Н1 1 0

Выдвинутые гипотезы проверяются следующим образом:

1) если модуль наблюдаемого значения t-критерия больше критического

значения t-критерия, т. е. |tнабл| > tкрит, то с вероятностью (1 −α) или γ основную гипотезу о незначимости параметров регрессии отвергают, т. е. параметры регрессии

не равны нулю;

2) если модуль наблюдаемого значения t-критерия меньше или равен

критическому значению t-критерия, т. е. |tнабл| ≤tкрит, то с вероятностью α или (1 −γ) основная гипотеза о незначимости параметров регрессии принимается, т. е.

параметры регрессии почти не отличаются от нуля или равны нулю.

Формула наблюдаемого значения t-критерия Стьюдента для проверки

гипотезы	Н0			0	имеет вид:
			1				~
					tнабл		1
		~					( 1 )
где				— оценка параметра регрессии β1;
		1

ω(β1) — величина стандартной ошибки параметра регрессии β1.

В случае парной линейной модели регрессии показатель вычисляется следующим образом:

	n
( 1 )	ei2
	n
	i 1
	(n 2) (xi x)2
	i 1

Числитель стандартной ошибки может быть рассчитан через парный коэффициент детерминации как:

n	n	~
2			2	n G	2	2
ei	( yi yi )					( y) (1 rxy )
i 1	i 1

где G2 ( y) - общая дисперсия зависимого признака;

rxy2 - парный коэффициент детерминации между зависимыми и независимыми признаками.

Вычисляя критического значения t-критерия, получили tкрит=-6,901 и сравниваем с критическими tкрит, которые определяют по таблице распределения Стьюдента с учётом принятого уровня значимости α=0,95 и числом степеней свободы вариации n–2 (15-2=13), получили tкрит=1,7715.

Наблюдаемое значение t-критерия по модулю больше его критического значения, т. е. |tнабл| > tкрит. Таким образом, коэффициент парной регрессии 1 оказался значимым.

Формула наблюдаемого значения t-критерия Стьюдента для проверки

	гипотезы	Н0			0 имеет вид:
				0			~
					tнабл		0
			~				( 0 )
	где				— оценка параметра регрессии β0;
				0

ω(β0) — величина стандартной ошибки параметра регрессии β0.

В случае парной линейной модели регрессии показатель вычисляется следующим образом:

	n	n
( 0 )	ei2	xi2
		n
	i1	i1
	n (n 2) (xi x)2
	i1

Проверка гипотезы о значимости парного линейного коэффициента корреляции

При проверке значимости коэффициента корреляции между независимым признаком x и зависимым признаком y (предположения того, что изучаемый параметр отличается от нуля), выдвигается основная гипотеза H0 о его незначимости:

Н0 rxy 0 ; в качестве альтернативной (или обратной) выдвигается гипотеза H1 о

значимости коэффициента корреляции: Н1 rxy 0 .

Для проверки выдвинутых гипотез используется t-критерий (t-статистику) Стьюдента.

Критическое значение t-критерия tкрит(α; n−h), где α — уровень значимости, (n − h) — число степеней свободы, определяется по таблице распределений t-критерия Стьюдента.

Формула значения t-критерия Стьюдента для проверки гипотезы Н0 rxy 0

имеет вид:

tнабл rxy

(rxy )

(rxy ) - величина стандартной ошибки парного выборочного коэффициента

корреляции.

При линейной парной модели регрессии эта величина рассчитывается как:

	1 r 2
(rxy )	xy
	n 2

Подставим данную формулу в выражение для расчета наблюдаемого значения t-критерия Стьюдента для проверки гипотезы Н0 rxy 0 , получим:

tнабл			rxy			(n 2)
		1		r 2
				xy

Необходимо сделать проверку значимости коэффициента корреляции.

Проверка гипотезы о значимости уравнения парной регрессии

Для проверки гипотезы значимости уравнения регрессии в целом используется F-критерий Фишера—Снедекора.

Гипотеза проверяется следующим образом:

1)если наблюдаемое значение F-критерия больше критического значения

данного критерия, т. е. Fнабл > Fкрит, то с вероятностью α основная гипотеза о незначимости коэффициентов уравнения регрессии или парного коэффициента детерминации отвергается, и уравнение регрессии признается значимым;

2)если наблюдаемое значение F-критерия меньше критического значения

данного критерия, т. е. Fнабл < Fкрит, то с вероятностью (1 −α) основная гипотеза о незначимости коэффициентов уравнения регрессии или парного коэффициента детерминации принимается, и построенное уравнение регрессии признается незначимым.

Критическое значение F-критерия находится по таблице распределения Фишера—Снедекора в зависимости от следующих параметров: уровня значимости α

ичисла степеней свободы: k1=h−1 и k2=n−h, где n — это объем выборки, а h — число оцениваемых по выборке параметров. В случае проверки значимости уравнения

парной регрессии критическое значение F-статистики вычисляется как Fкрит(α; 1; n −

2).

Формула наблюдаемого значения в случае парной регрессии наблюдаемое значение F-критерия имеет вид:

r 2

Fнабл xy 2 (n 2) 1 rxy

Необходимо сделать проверку значимости уравнения регрессии.

Сделать вывод о значимости построенного уравнения регрессии.

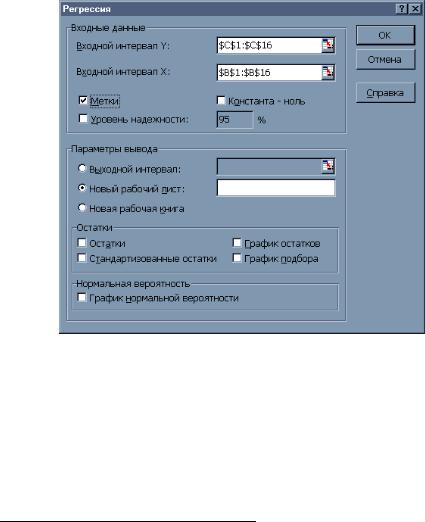
В подтверждение расчетов необходимо сравнить с расчетами, полученными с использованием встроенных функций Exсel. Использование встроенных функций, да и точечных диаграмм, имеет определенные ограничения, поскольку нет функций, вычисляющих стандартные отклонения коэффициентов регрессии и значение детерминации. Поэтому рассмотрим дополнительные возможности, которые доступны с помощью надстройки Анализ данных. Данная надстройка подключается с помощью пункта меню Сервис, Надстройки и запускается на выполнение с помощью пункта меню Сервис, Анализ данных. После выбора надстройки Регрессия появится диалоговое окно (рис. 3).

Данное диалоговое окно имеет множество дополнительных переключателей, которые приводят к выводу большого количества дополнительной информации.

Основные параметры, которые необходимо задать — это Входной интервал Y и

Входной интервал X, а также Параметры вывода. Если количество данных Y и X

совпадает, то выдаются итоги построения модели парной регрессии (именно этот случай будем сейчас рассматривать), а если число переменных X в несколько раз больше числа Y, то — модель множественной регрессии. В противном случае будет выдано сообщение об ошибке. Если активизировать переключатель Метки, то во входные интервалы для X и Y можно добавить ячейки с названиями, и соответствующие метки появятся в итоговой таблице, что значительно облегчит её понимание.

Рис. 31

Если Входной интервал Y определить как C1:C16, а Входной интервал X —

B1:B16, задать некоторым образом параметры вывода, а также установить опцию Метки, то автоматически на новом листе будет сгенерированна таблица 2.

Таблица 2

ВЫВОД ИТОГОВ

Регрессионная статистика

Множественный R	0,887036
R-квадрат	0,786833
Нормированный
R-квадрат	0,770435
Стандартная
ошибка	2,264609
Наблюдения	15

					Продолжение табл. 1
Дисперсионный анализ
					Значимость
	df	SS	MS	F	F
Регрессия	1	246,0889	246,0889	47,985	1,04E–05
Остаток	13	66,66991	5,128455
Итого	14	312,7588
		Стандартная	t-	P-	Нижние	Верхние
	Коэффициенты	ошибка	статистика	значение	95 %	95 %
Y-пересечение	240,142	17,70861	13,56075	4,76E–09	201,8849	278,3991
Цена x (р.)	–7,71453	1,113671	–6,92712	1,04E–05	–10,1205	–5,30859

Задача № 2

Требуется для характеристики зависимости У от X рассчитать параметры линейной (альтернативным методом нахождения параметров уравнения парной регрессии ), степенной, показательной функции и выбрать оптимальную модель (провести оценку моделей через среднюю ошибку аппроксимации (А) и F- критерий Фишера).

Решение:

Построение линейной функции альтернативным методом нахождения параметров уравнения парной регрессии вида y y yx (x x) сводиться к

нахождению параметра:

yx ryx Sx

S y

где ryx – линейный коэффициент парной корреляции между переменными y и

x;

Sx, Sy – среднеквадратическое отклонение величин y и x.

Построение степенной функции ( y 0 x 1 ), показательной функции ( y 0 1x )

и уравнения равносторонней гиперболы ( y 0	1	1	) разрешается путем их
		x
линеаризации и введения замены:

y 0 x 1 → Ln( y) Ln( 0 ) 1 Ln(x) →Y Ln( 0 ) 1 X

y 0 1x → Ln( y) Ln( 0 ) x Ln( 1 ) →Y Ln( 0 ) x Ln( 1 )