Lektsii (1) / Lecture 23

ICEF, 2012/2013 STATISTICS 1 year LECTURES

Лекция 23

05.03.13

Мы изучили ситуацию, когда генеральная совокупность описывается дискретной случайной величиной. Как модифицируется тест, если генеральная совокупность − это непрерывная случайная величина, например, X N (2,3) ?

Рассмотрим этот пример подробнее. Пусть Х − непрерывная генеральная совокупность. Нулевая гипотеза H0: X N (2,3) , альтернатива Hа − отрицание H0.

Разобьём всю область значений случайной величины на k отрезков

∆j	= (a j−1, a j ], j =1,..., k . Поскольку в нашем случае эта область − вся числовая прямая, то
a0	= −∞, ak = +∞. При нулевой гипотезе можно вычислить вероятности
	a		j−1	−2		a	j	−2
πj	= Pr(X ∆j ) = Pr(a j−1 < X ≤ a j ) = Pr				< Z ≤					, j =1,..., k .
			3					3

Всегда должно быть ∑k π j =1.

j=1

Пусть x1,..., xn − выборка из генеральной совокупности. Для каждого отрезка ∆j посчитаем количество наблюдений, попавших в этот отрезок:

Oj = #{i : xi ∆j , i =1,..., n}, j =1,..., k				(Observed) , и ожидаемые: E j = n πj , j =1,..., n
(Expected). Очевидно, что ∑k			Oj = ∑k	E j = n .
		j=1	j=1
Составим статистику
χ2 = ∑k	(Oj −E j )2	.
j=1	E j
Так же, как и в дискретном случае, справедлива

Теорема. При нулевой гипотезе статистика χ2 имеет при больших n распределение

χ2 (k −1) .

Таким образом, тест устроен так:

1) построить разбиение ∆j = (aj −1, aj ], j =1,..., k и вычислить статистику

	χ2 = ∑k	(Oj −E j )2	;
		E j
	j=1

2) вычислить P-value и на этом основании сделать статистический вывод. Принципиальное отличие от дискретного случая состоит в том, что как количество отрезков разбиения, так и сами отрезки, можно выбирать по-разному. Утверждение теоремы от разбиения не зависит, поскольку оно носит асимптотический характер, т.е. при n →∞. Однако на практике, имея одну выборку x1,..., xn , но, выбирая разные наблюдения,

можно получать разные выводы. Не забываем условия применимости нормального приближения: надо так выбирать разбиение, чтобы в каждом отрезке было больше пяти наблюдений: Oj >5, j =1,..., k .

Пример. Дана выборка объёма n =50

5.09	7.70	8.10	8.73	9.30	9.65	10.15	10.60	11.49	12.24
6.49	7.75	8.16	8.74	9.40	9.72	10.21	10.74	11.83	12.32
7.04	7.98	8.46	8.96	9.42	9.82	10.49	11.09	12.00	12.88
7.12	8.03	8.51	9.09	9.47	9.88	10.54	11.18	12.03	12.94
7.30	8.09	8.59	9.13	9.50	9.96	10.59	11.32	12.08	13.29

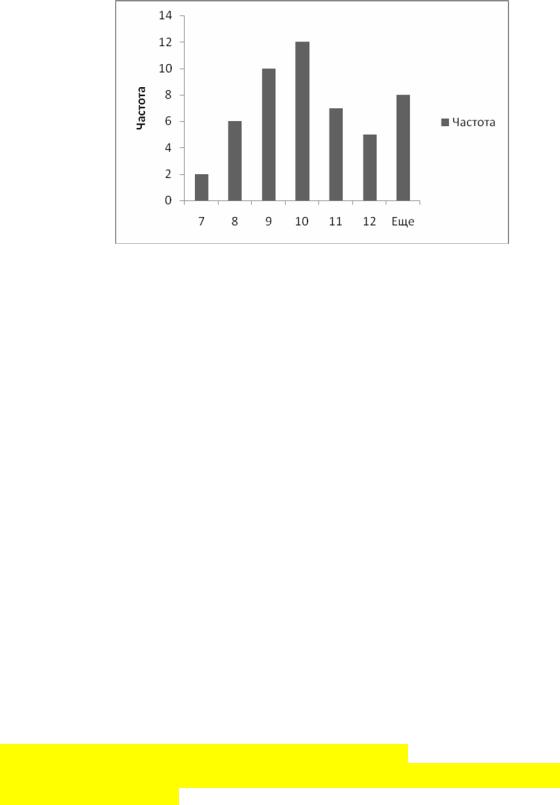
Выборочное среднее x =9.70 , выборочное стандартное отклонение s =1.82 . Ниже дана гистограмма этой выборки.

Проверим гипотезу, что генеральная совокупность Х является нормальной со средним 10 и стандартным отклонением 2, т.е.

H0 : X N (10, 2) .

Разобьём числовую прямую на семь отрезков:

∆1 = (−∞,7], ∆2 = (7, 8], ∆3 = (8,9], ∆4 = (9,10], ∆5 = (10,11], ∆6 = (11,12], ∆7 = (12, +∞) .

Используя компьютер (или калькулятор, или таблицы…) находим вероятности

πj = Pr(X ∆j ), j =1,...,7 при нулевой гипотезе:

π	0.067	0.092	0.150	0.191	0.191	0.150	0.159	и вычисляя
Подсчитывая количество наблюдений Oj , попавших в каждый отрезок ∆j

ожидаемые значения E j = n πj , окончательно получаем следующую таблицу:

		(O −E)2	χ2
O	E	E		P-vauel
2	3.340	0.538	3.945	0.684
6	4.592	0.431		d.f.=6
10	7.494	0.838
12	9.573	0.615
7	9.573	0.692
5	7.494	0.830
8	7.933	0.001

Нулевая гипотеза не отвергается на любом разумном уровне значимости.

Справедливости ради следует заметить, что в первых двух отрезках наблюдаемые значения меньше 5. Это, конечно, неточность, но лень переделывать.

Упражнение. Повторите процедуру для другого разбиения

∆1 = (−∞,7.5], ∆2 = (7.5, 9], ∆3 = (9,10], ∆4 = (10,11.5], ∆5 = (11.5,13], ∆6 = (13, +∞) .

Изменится ли ваш вывод?

CHI-SQUARE TESTS FOR INDEPENDENCE.

CONTINGENCY TABLES

Разновидностью хи-квадрат тестов являются так называемые chi-square tests for independence или chi-square tests of association. Как и раньше, проще пояснить суть этого теста на примере.

Пример. Исследователя интересует, одинаково ли распределен доход в разных регионах страны. Предположим для простоты, что есть всего два региона − South and North, а доход разбит на четыре уровня − < $5 000, $5 000 − $10 000, $10 000 − $15 000, > $15 000.

Случайным образом были выбраны 400 человек, и их распределение по регионам и уровням дохода представлены в таблице:

			Income ($1000)
Region	0 − 5	5 − 10	10 − 15	>15	Total
South	28	42	30	24	124
North	44	78	78	76	276
Total	72	120	108	100	400

Например, число 28 означает, что в данной выборке 28 человек живут на юге и имеют доход менее $5 000. Число 124 в столбце Total, очевидно, общее число жителей юга в выборке.

Можно ли утверждать, что распределение дохода на юге и на севере одинаково или, что эквивалентно (это вы докажете сами, решив одну из задач очередного домашнего задания), эти два фактора − доход и регион − независимы.

В данном случае популяция − это два случайных фактора (совместное распределение): Region, принимающий два значения и Income, принимающий четыре значения. Обозначим πij , i =1, 2, j =1, 2,3, 4 − совместное популяционное распределение. (Напомним, что,

например, π23 − это доля людей, живущих на севере и имеющих доход от $10 000 до

$15 000, или, что то же самое, − это вероятность того, что наугад выбранный из популяции индивидуум будет жить на севере и иметь третий уровень дохода.) Тогда, как мы знаем, независимость факторов означает, что

H0 :πij =πii πi j ,

где πii, πi j − соответствующие маржинальные распределения. Особенность задачи в том, что мы не знаем числа πii, πi j , но можем их оценить с помощью соответствующих

выборочных пропорций:

p1i = 124400 = 0.31, p2i = 276400 = 0.69 =1−0.31;

pi1 = 40072 = 0.18, pi2 = 120400 = 0.30, pi3 = 108400 = 0.27, pi4 = 100400 = 0.25 =1− pi1 − pi2 − pi3 .

Тогда (оцененное) ожидаемое число в ячейке (i, j) при нулевой гипотезе есть

Eij = n pii pi j .

Таблица ожидаемых значений:

			Income ($1 000)
Region	0 − 5	5 − 10	10 − 15	>15	Total	Marginal Region
South	22.32	37.2	33.48	31	124	0.31
North	49.68	82.8	74.52	69	276	0.69
Total	72	120	108	100	400
Marginal Income	0.18	0.3	0.27	0.25

Как и раньше, составляем статистику

	2	4	(O −E )2
	χ2 = ∑∑		ij ij	,	(1)
			Eij
	i=1	j=1

суммируя как по столбцам, так и по строкам таблиц. В данном случае χ2 =5.81. Теорема. При нулевой гипотезе статистика (1) асимптотически (при больших n) имеет распределение χ2 , число степеней которого равно произведению (r −1)(c −1) , где r − число строк, с − число столбцов.

Внашем случае d.f. = (2−1)(4−1)=3. P-value = 0.121. На 5%-ном уровне значимости нулевая гипотеза не отвергается.

Таблицы, используемые в этом тесте называются таблицами сопряжённости, Contingency Tables.

Вобщем случае, имеется два признака (фактора) А и В. Первый имеет r значений a1,...,ar ,

второй c значений b1,...,bc . Пусть π1•,...,πr•, π•1,...,π•c	− популяционные частоты значений
признаков А и В, соответственно. Пусть πij , i =1,..., r,	j =1,..., c − популяционные частоты

совместного распределения признаков А и В. Тогда нулевая гипотеза о независимости признаков может быть записана так: Н0: πij =πi•π• j .

У нас есть п наблюдений (x1, y1 ),...,(xn , yn ) , и пусть

Oij = #{(xm , ym ) : xm = ai , ym =bj , m =1,..., n} (наблюдаемые, observed). Если бы πij были известны, то ожидаемое (expected) число с признаками (i, j) было бы равно

Eij =πijn =πi•π• jn при нулевой гипотезе. Однако при неизвестных частотах мы оцениваем

			n		n• j	c	r
их естественным образом: pi•	=		i•	, p• j =		, ni• = ∑nij , n• j = ∑nij . Таким образом,
					n
			n			j=1	i=1
оценивается l = (r −1) +(c −1)	независимых параметров. Число степеней свободы
d. f . = rc −1 −(r −1) −(c −1) = (r −1)(c −1) .
Общее правило: d. f . = number		of cells −1−number of					estimated parameters

При практическом использовании нужно следить за выполнением условий применимости нормального приближения, которые в данном случае имеют вид:

1)n > 40 ,

2)Oij >5 .

Модель парной регрессии (simple regression, гл.12)

До сих пор мы изучали одиночный фактор. Модель парной регрессии − это одна из простейших моделей, в которой рассматривается взаимодействие двух факторов. Рассмотрим пример.

Пример. Пусть нас интересует связь между месячным семейным доходом (Income = I) и ежемесячными семейными расходами на питание (Food Expences = FI). В данном случае генеральная совокупность − это множество всех доступных для наблюдения семей. С каждой семьей связана пара чисел (I, FE). Условно говоря, мы считаем доход I независимой переменной, а расходы на питание FE − зависимой переменной. Ясно, что

детерминированной связи между I и FE нет: если рассмотреть под-популяцию семей, имеющих заданный уровень дохода I0 , то расходы на питание в ней у разных семей

будут, вообще говоря, разные. Иными словами, есть распределение величины FE в рассматриваемой под-популяции.

Так же, как и раньше, когда мы рассматривали только одну генеральную совокупность (популяцию) Х и интересовались ее средним значением E(X ) , сейчас фокус наших

интересов − это среднее значение зависимой переменной в каждой под-популяции, характеризуемой уровнем I независимой переменной, т.е. величина E(FE | I ) . Но теперь

это не число, а функция ϕ(I ) = E(FE | I ) , зависящая от I. Основная задача состоит в восстановлении (оценивании) функции ϕ(I ) по наблюдениям (Ii , FEi ), i =1,..., n , взятым из рассматриваемой популяции.