Раздаточные материалы - 2003 / solid

ЭЛЕКТРОННАЯ СТРУКТУРА ТВЕРДЫХ ТЕЛ

Твердое тело можно рассматривать как очень большую молекулу, в которой соблюдается либо дальний (идеальный), либо ближний порядок расположения атомов или молекул. Первый случай отвечает идеально регулярным кристаллам, симметрия которых описывается 230 федоровскими пространственными группами. Второй – более общий - случай охватывает реальные кристаллы с дефектами кристаллической решетки, аморфные тела, полимеры и т.д.: для них характерна лишь локальная симметрия определенных фрагментов. Для каждого из упомянутых случаев существуют свои способы описания электронной структуры. Идеально регулярные кристаллы считаются бесконечными (наличие поверхности игнорируется) и их волновые функции определяются с явным учетом трансляционной симметрии кристалла. В кристаллах с ближним порядком часто достаточно использовать модифицированные молекулярные модели, выделив некоторый атомный или молекулярный фрагмент – кластер. Рассмотрим оба этих подхода подробнее.

Одноэлектронные волновые функции в бесконечных периодических кристаллах и методы их расчета

Симметрийные свойства идеальных кристаллов состоят в следующем.

В идеальном кристалле всегда можно ввести три вектора трансляций: a,b и c так, что физические свойства кристалла в некоторой произвольно выбранной точке r точно воспроизводятся в любой другой точке r удовлетворяющей условию

( 1 )

где n₁, n₂, n₃ —произвольные целые числа. Совокупность точек r, определяемая выражением (1), при различных n₁, n₂, n₃ дает кристаллическую решетку, которая описывает регулярное периодическое расположение точек в пространстве.

Параллелепипед, имеющий в качестве ребер вектора : a,b и c , называется

элементарной ячейкой ( рис. 1). Перемещение всего кристалла как целого параллельно самому себе, описываемое вектором Т, называется трансляцией. Вектор трансляции кристаллической решетки связывает любые две точки ре- шетки.

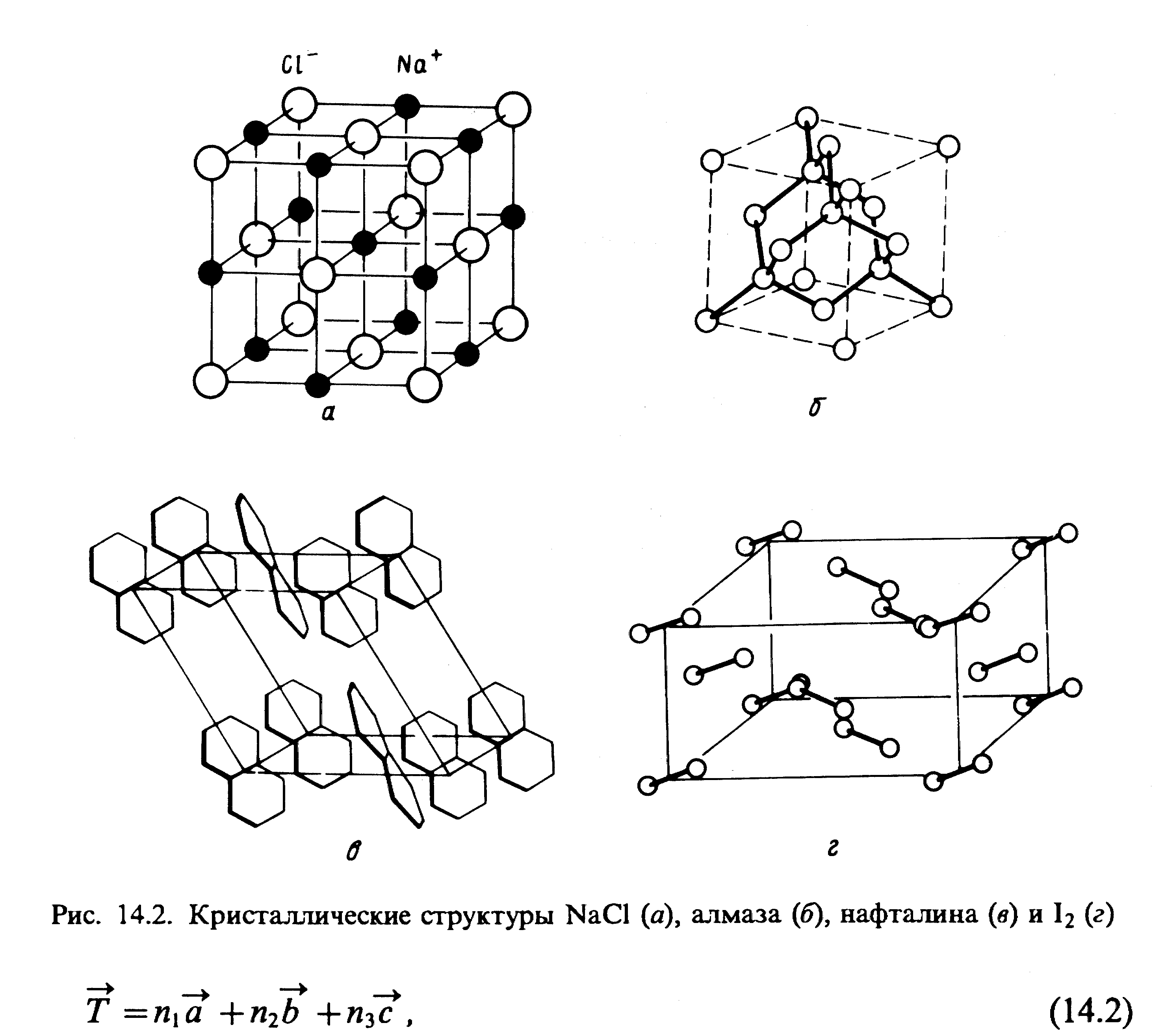
Посредством соответствующих операций трансляций элементарной ячейкой можно заполнить все пространство кристаллической структуры. Такое свойство кристалла названо трансляционной симметрией. На рис. 2 представлены структуры некоторых атомных и молекулярных кри­сталлов.

Трансляционная симметрия предполагает бесконечную протяженность кристалла. Конечно, регулярные структуры не являются бесконечными, а при отсутствии бесконечности теряется важное свойство трансляционной симметрии.

Один из способов сохранения трансляционной симметрии конечных систем - наложение циклических граничных условий (условия Борна-фон-Кармана). Суть их в том, что эквивалентные группы атомов отож­дествляются друг с другом так, чтобы граница отсутствовала.

В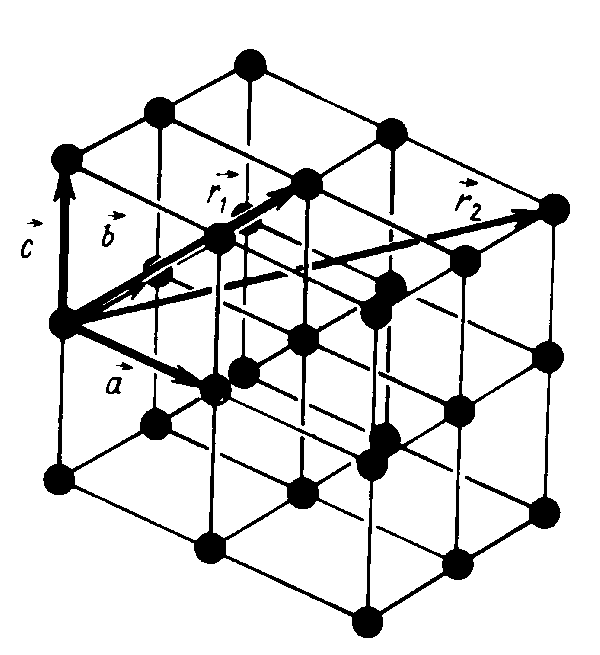 ажнейшие электронные свойства периодических кристаллов хорошо видны уже в случае одномерных систем. Для цепочки атомов это это равносильно изгибу цепочки в окружность большого радиуса и соединение между собой концевых атомов. Рассмотрим цепочку, состоящую из атомов, разделенных расстоянием а и имеющих один валентный электрон ( Li, Na, Ka и т.д.), описываемый атомной орбиталью (х). Каждое ядро в этих атомах хорошо экранировано внутренними электронами и валентный электрон лишь слабо связан со «своим» остовом. Влияние соседних атомом в цепочке приводит к тому, что валентные электроны могут передвигаться от атома к атому, как если бы они были свободными (модель почти свободных электронов Зоммерфельда). Волновая функция свободного электрона есть бегущая волна exp(ikx), а его кинетическая энергия равна

Е_кин= p²/2m=(kh)²/8²m ( 2)

(k=2/ - волновое число или квазиимпульс электрона). Специфика нашей задачи состоит в том, что движение электрона происходит в слабом периодическом потенциале, вид которого обусловлен сортом и расположением атомов в решетке. Это означает, что потенциал V(x) в уравнении Шредингера

[T(x) + V(x)] u_k(x) = Eu_k(x) ( 3 )

обладает свойством V(x)=V(x+na), где n=0,1, 2, … Учет этого обстоятельства при решении уравнения Шредингера приводит к тому, что волновая функция электрона в периодическом потенциале u_k(x) имеет вид модулированной зависящей от волнового числа k бегущей волны

u_k(x)=N _n exp(ikan)( x + na) ( 4 )

(N – нормировочный множитель), которая также периодична в решетке: (x) = (x+na) и сдвиг цепочки на величину, кратную а, не меняет u_k. Функция u_k, играющая в твердом теле роль атомной орбитали, называется функцией Блоха. При k =  b/a волновые функции электрона уже не являются бегущими волнами типа exp(  ikx). Так, при b=0  k=0 и

u₀(x)=N [( x )+( x + a)+ (x + 2a)+ (x + 3a) +…] , ( 5 )

а при b=1  k=  /a и

u_/a (x)=N [( x )-( x + a)+ (x + 2a)- (x + 3a) +…] (6 )

( см. рис.3) . В первом случае АО на разных атомах интерферируют в фазе и результирующая функция Блоха является связывающей и отвечает более низкой энергии. Второй случай отвечает деструктивной интерференции АО и,

a) k = 0 u₀ = N [ (x) + (x + a) + ....]

б) k = + /a u_/a = N [ (a) - (x + a) +  .....]

Рис.3

соответственно, - разрыхляющей функции Блоха. Таким образом, волновые функции электрона в периодическом потенциале можно ассоциировать со стоячими волнами вида u₁=sinx/a и u₂ =cosx/a , каждая из которых есть сумма бегущих волн (рис. 4). Эти стоячие волны имеют узлы и пучности в разных областях пространства по отношению к создающим внешний потенциал атомным остовам. Это значит, что они отвечают концентрации электронов (которая пропорциональна u²) в местах, отвечающих различным значениям потенциальной энергии. Так, u₂ описывает концентрации электронов вблизи остовов, где потенциальная энергия минимальна, а u₁ - между остовами.

Число возможных значений k определяется числом узлов кристаллической решетки. Область в k –пространстве, лежащая между  /a, называется первой зоной Бриллюэна. Поведение электронов в более высоких зонах Бриллюэна

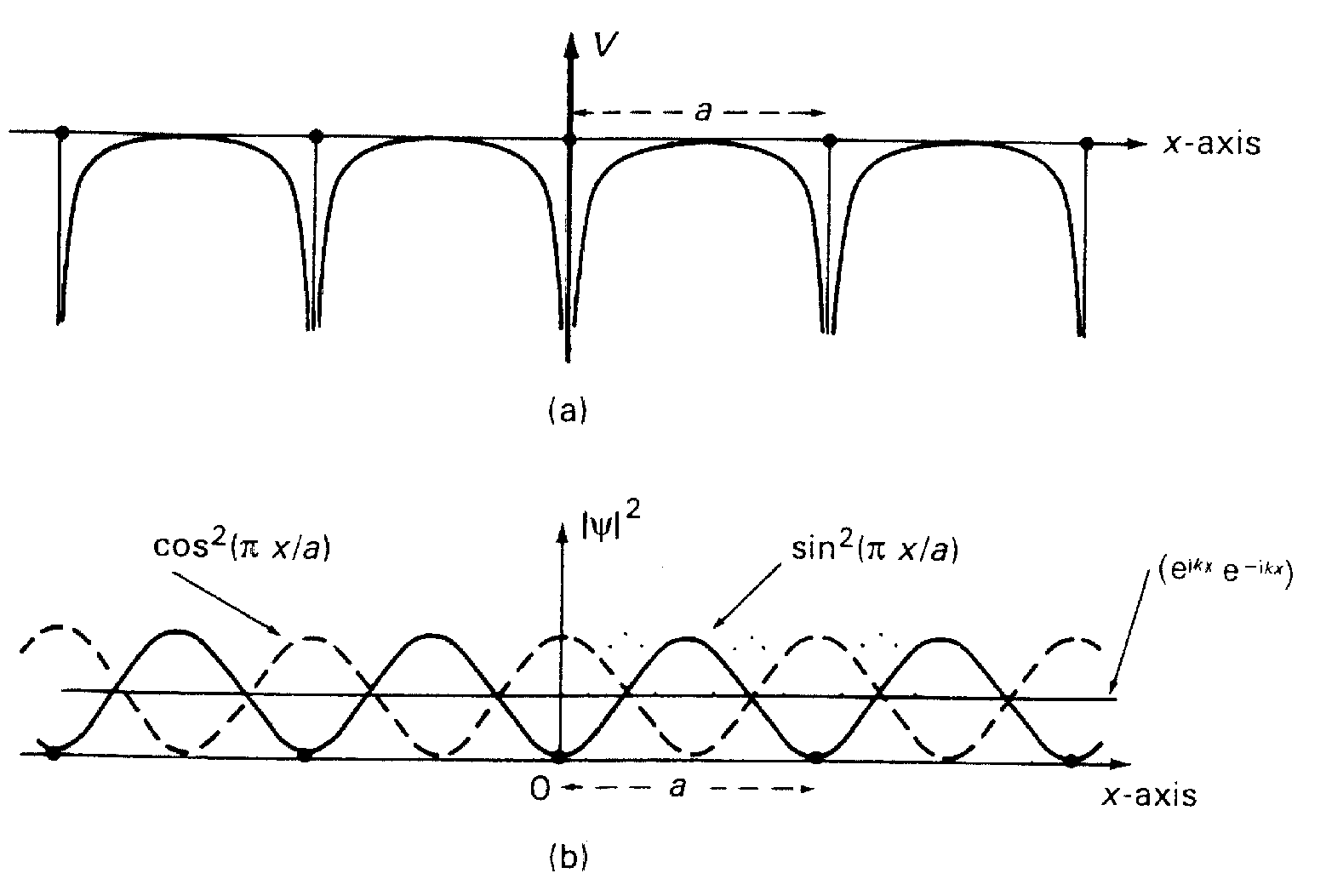Рис.4

получено из информации о первой зоне (рис.5). В пределах первой зоны Бриллюэна энергия по-прежнему имеет вид, близкий к (2). Однако на границах зон Бриллюэна среди возможных (“разрешенных”) значений энергии появляются разрывы из-за того, что средняя потенциальная энергия электрона, описываемого функцией u₂ меньше, чем для случая u₁. Разность энергий E_g называется энергетической щелью.

рис.5

Кристаллические орбитали – аналоги МО – строятся из функций Блоха (4), которые таким образом играют в кристалле роль базисных функций:

_k (r ) =  c_j(k) u_kj(r) (7)

Т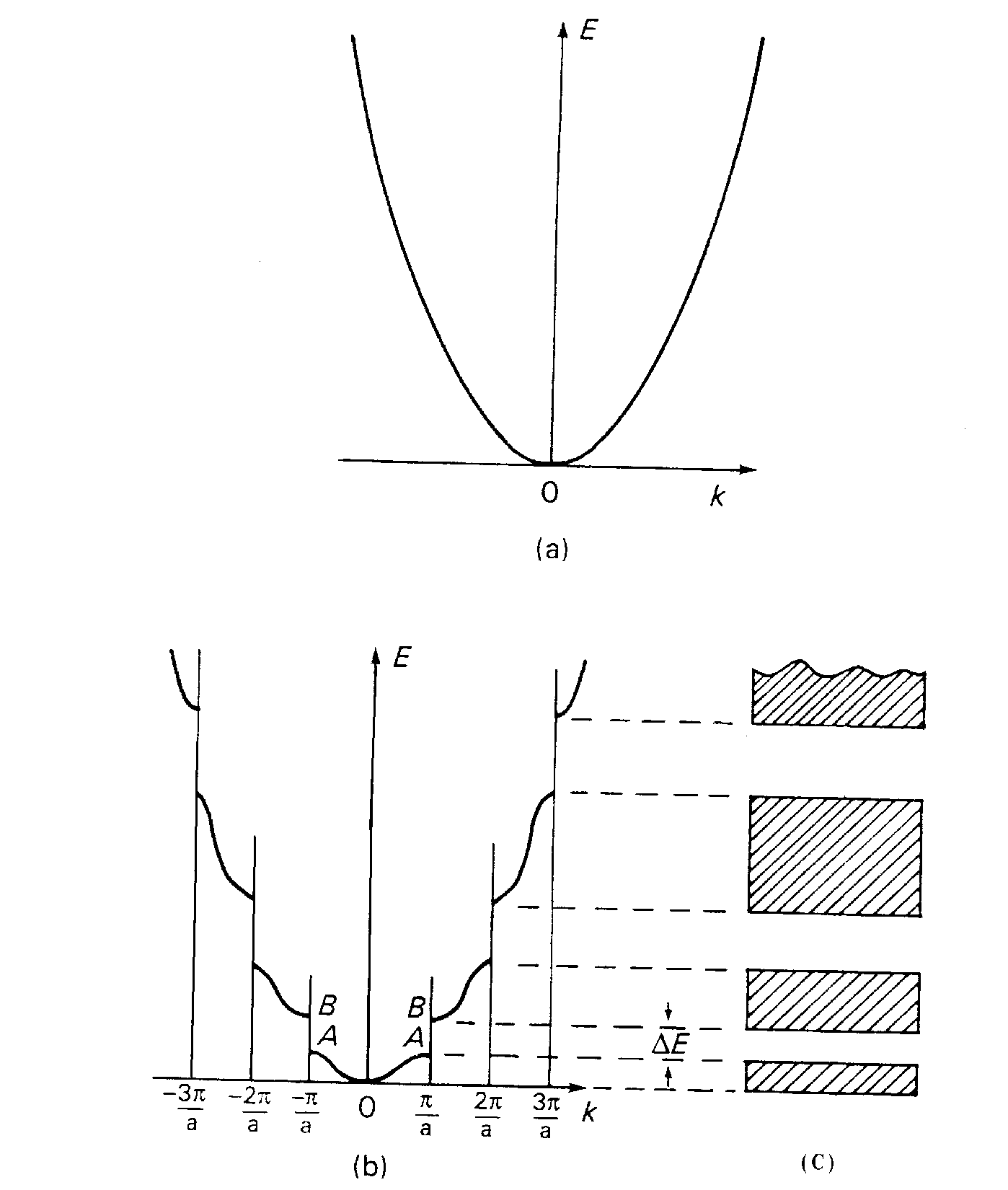 аким образом, электроны в кристалле оказываются распределенными по энергетическим полосам (зонам), состоящим из уровней энергии, отвечающих волнам с разрешенными симметрией волновыми векторами. Расстояния между энергетическими уровнями на краях зоны меньше, чем в середине, т. е. плотность уровней (число уровней на единицу энергии) не одинакова по всей зоне: у краев зоны плотность выше. Для описания зависимости расстояния между уровнями от k предполагают непрерывное заполнение зоны (полосы) энергетическими уровнями и вводят непрерывную функцию Е(k), которую называют также структурой полосы. Она описывает закон дисперсии энергии. Высшая орбиталь в твердом теле, заполненная электронами, называется уровнем Ферми.

Распределение энергетических уровней в зоне характеризует плотность состояний:

D(E) = dN(E)/dE (8)

Интегрирование D(E) по dE до уровня Ферми дает полное число кристаллических орбиталей.

Разность между высшим и низшим энергетическими уровнями называют шириной зоны (полосы), она также характеризует дисперсию энергии. Ширина зоны определяется величиной взаимодействия между атомами в сосед­них ячейках и зависит от соответствующих интегралов перекрывания АО.

Промежуток, между верхней энергетической зоной, заполненной элект-ронами (валентной), и нижней, не заполненной электронами (зоной проводи-мости) называется запрещенной зоной.

От того, как заполнена валентная зона и какова ширина запрещенной зоны, зависят многие свойства веществ. Зона Бриллюэна содержит столько разрешенных значений k- векторов ( а значит, столько различных волновых функций), сколько элементарных ячеек N в кристалле. Если кристалл образовался из

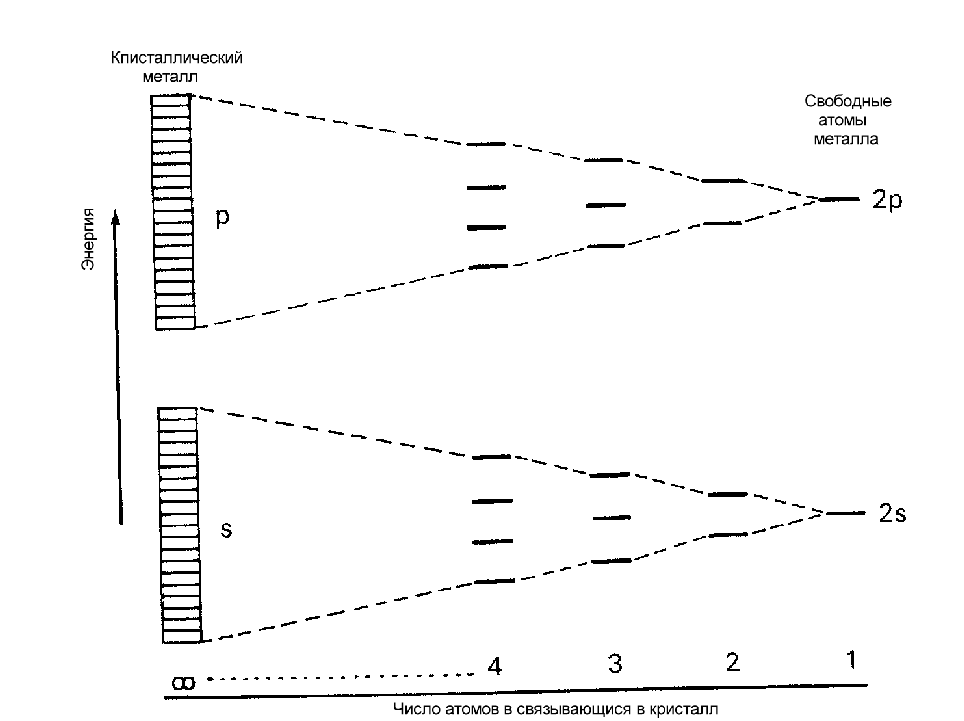
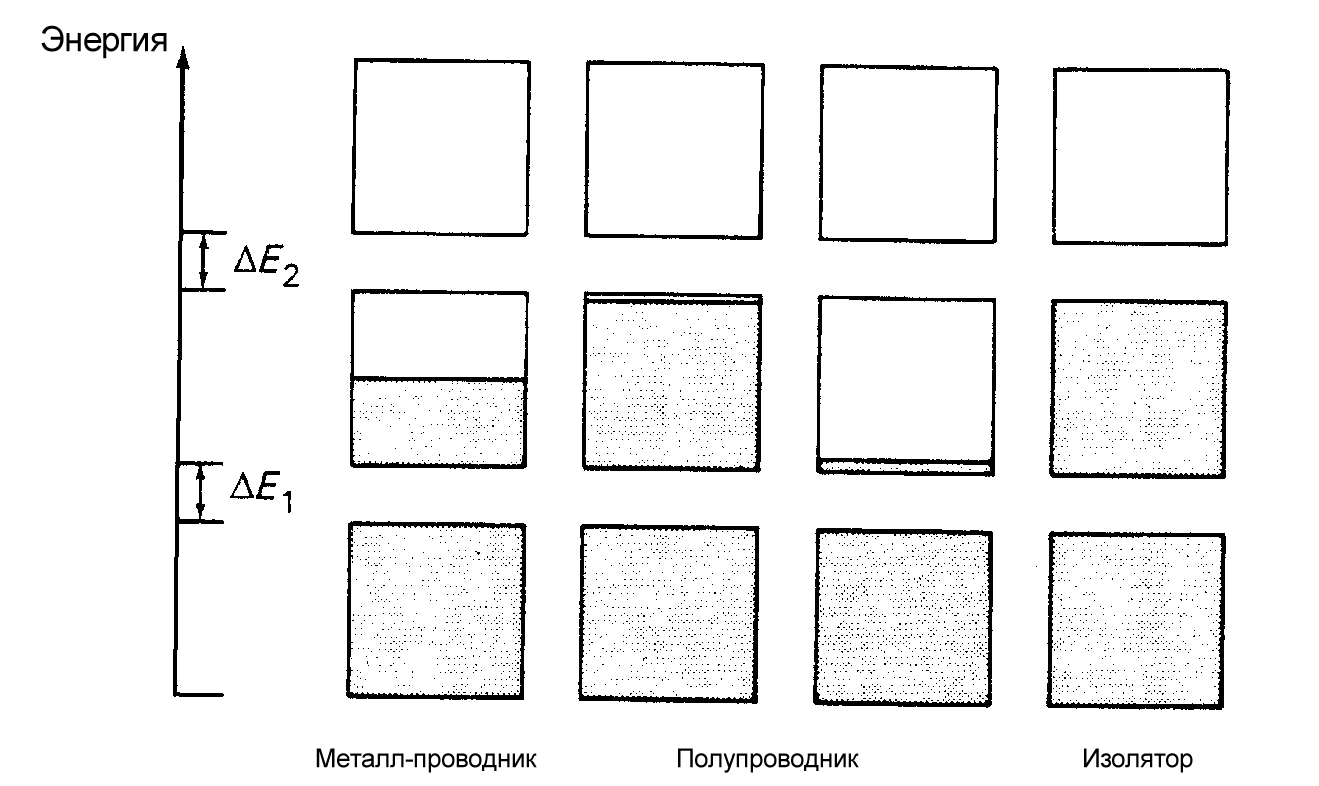
атомов с g валентными электронами (g=1 для s оболочки; g=3 для p оболочки и т.д.), то зона состоит из Ng энергетических уровней, каждый из которых может

быть занят 1 или 2 электронами (рис.6). Если валентная зона полностью запол-нена электронами, а ширина запрещенной зоны Е_g  2 эВ, то вещество называется диэлектриком. Если валентная зона полностью заполнена электронами, а ширина запрещенной зоны Е_g 2 эВ, то вещество называется полупроводником.

Если валентная зона заполнена электронами частично либо перекрывается с зоной проводимости, то вещество называется металлом.

Для расчета одноэлектронных волновых функций в кристаллах используют два основных метода.

1. Метод Хартри-Фока. Функции (4) используются как базисные и строятся из атомных орбиталей ( как правиоло, ОСТ). Недостатки: из-за учета только корреляции Паули переоценивает ширину запрещенной зонв в 1,5-2 раза; неприменим для расчета Ферми-поверхности металлов.

2. Метод Кона-Шэма – относится к группе методов функционала плотности.

Основан на предположении, что электронную плотность можно рассматривать как неоднородный электронный газ, определяющий обменно-корреляционные эффекты. Одноэлектронные уравнения имеют вид ( атомные единицы)

[ -1/2² + V_N(r) +(r)/(r- r)dr +V_xc ] _k (r ) = E(k)_k (r ) (9)

Здесь V_N –потенциал ядер, V_xc – обменно-корреляционный потенциал,для которого используются различные приближения – функционалы ЭП. Базисные функции различны: это могут быть как комбинации атомных орбиталей, так и наборы плоских волн. Недостаток: недооценка ширины запрещенной зоны.

Кластерные методы

Часто ( например, при расчетах нестехиометрических кристаллов) целесообразно рассчитать лишь некоторый атомный или молекулярный фрагмент кристалла – кластер. Основной метод, используемый для это цели– метод Хартри-Фока.

Одна из распространенных его кластерных модификаций – так называемый X_-метод. Корреляция электронов здесь по-прежнему игнорируется, а обменный потенциал представляется в виде

V_x(r ) = -3((3/8)(r ))^1/3 (10)

Несмотря на кажущуюся переупрощенность, X_-метод дает хорошее количественное описание не только локализованных состояний, но и зонной структуры твердых тел. Для этого используют метод «погруженного» кластера: одноэлектронные функции раскладывают по базису из локализованных орбиталей и функций Блоха. Метод успешно применяется для изучения магнитных свойств веществ, химической связи и др.