
- •Шайкин а.Н.
- •Операции над строками матрицы
- •Ступенчатые матрицы
- •Отбросим первую строку. Оставшаяся матрица имеет строку. По индуктивному предположению ее можно привести к ступенчатому виду:
- •Линейная зависимость строк матрицы
- •Ранг матрицы. Базисные строки
- •Определители
- •Операции над матрицами
- •Обратная матрица
- •Системы линейных уравнений
- •Тогда в матричной записисистема линейных уравнений может быть записана в виде.
- •Специальный случай.
- •Раскладывая определитель по первой строке, имеем
- •Критерий совместности Вернемся к произвольной системе mуравнений сnнеизвестными.
- •Однородные системы
- •С использованием этой фундаментальной системы решений общее решение однородной системы записывается в виде , где– произвольные константы.

Шайкин а.Н.
МАТРИЦЫ
ОПРЕДЕЛИТЕЛИ
СИСТЕМЫ

Матрицы. Основные определения
Определение. Матрицей называется прямоугольная таблица, в каждой клетке которой стоит какое-нибудь число или выражение.
Матрицы обычно обозначают большими буквами латинского алфавита, например A, B, C.
Определение. Матрица имеет размерность m×n, если она имеет m строк и n столбцов.
Определение. Элементом матрицы называется содержимое ее клетки.
Элементы
матрицы обычно обозначают малыми буквами
латинского алфавита с двумя индексами,
где первый индекс – номер строки, а
второй – номер столбца, где элемент
расположен, например
![]() – элемент, расположенный на пересеченииi-й
строки и j-го
столбца.
– элемент, расположенный на пересеченииi-й
строки и j-го
столбца.
Матрицу обычно записывают следующим образом:
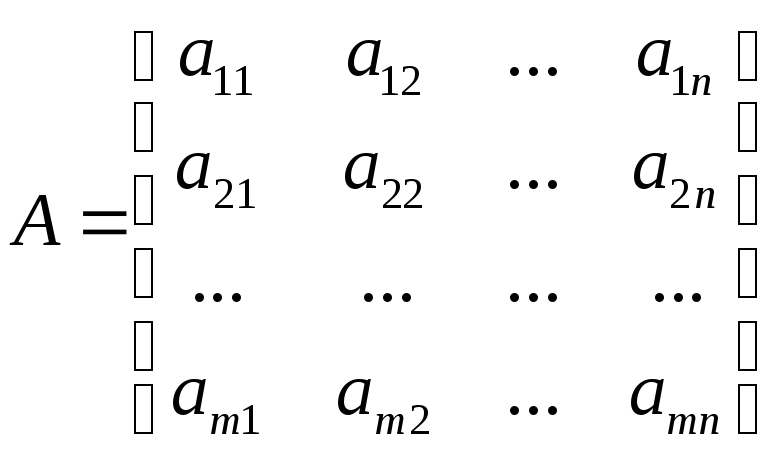 .
.
Определение. Матрицы называются равными, если они имеют одинаковую размерность и их элементы, стоящие на одинаковых местах, равны.
Определение. Матрица называется нулевой, если все ее элементы равны нулю.
Нулевую матрицу будем обозначать O (в то время как число – 0).
Определение. Матрицей-строкой называется матрица размерности 1×n. Ее также называют вектор-строкой.
Определение. Матрицей-столбцом называется матрица размерности m×1. Ее также называют вектор-столбцом.
Определение. Транспонированными называются матрицы, у которых строки (столбцы) одной являются столбцами (строками) другой. (Также говорят, что одна матрица получена из другой транспонированием).
Матрица,
полученная из матрицы A
транспонированием, будем обозначать
![]() .
.
Определение. Матрица называется квадратной, если число ее строк равно числу ее столбцов.
О размерности квадратной матрицы говорят одним числом, например квадратная матрица размерности n.
Определение.
Главную
диагональ
квадратной матрицы образуют элементы
![]() ,
,![]() ,
…,
,
…,![]() .
.
Определение.
Побочную
диагональ
квадратной матрицы образуют элементы
![]() ,
,![]() ,
…,
,
…,![]() .
.
Определение. Квадратная матрица называется диагональной, если все ее элементы, стоящие вне главной диагонали, равны нулю.
Определение. Квадратная матрица называется верхнетреугольной (нижнетреугольной), если все ее элементы, расположенные ниже (выше) главной диагонали, равны нулю.
Определение. Квадратная матрица называется единичной, если элементы ее главной диагонали равны единице, а все остальные – нулю.
Единичную матрицу будем обозначать E. Очевидно, что она является диагональной.
Операции над строками матрицы
Определение. Элементарными преобразованиями строк матрицы называются преобразования следующих трех типов:
1. перестановка местами двух строк.
Условное
обозначение:
![]() ,где стрелки
указывают на строки, переставляемые
местами.
,где стрелки
указывают на строки, переставляемые
местами.
2.
Замена строки
суммой этой строки и другой, предварительно
умноженной на какое-либо число
![]() .
.
Условное
обозначение:
![]() , где стрелка указывает на изменяемую
строку, а множитель
, где стрелка указывает на изменяемую
строку, а множитель![]() ставится рядом с преобразуемой строкой.
ставится рядом с преобразуемой строкой.
3.
Умножение
элементов строки на ненулевое число
![]() .
.
Условное
обозначение:
![]() , ставится рядом с преобразуемой строкой.
, ставится рядом с преобразуемой строкой.
Аналогично вводятся элементарные преобразования столбцов матрицы.
Ступенчатые матрицы
Определение. Опорным элементом строки матрицы называется первый слева ненулевой элемент этой строки.
Условное обозначение: обводится кружочком или квадратиком.
Определение. Матрица называется ступенчатой (имеющей ступенчатый вид), если опорный элемент каждой последующей строки расположен правее опорного элемента предыдущей.
В частности, опорный элемент первой строки может находиться в любом месте, нулевая строка (все элементы которой – нули) может располагаться под любой строкой, а ниже нулевой строки могут находиться только нулевые.
Определение. Матрица имеет ступенчатый вид Гаусса, если:
она имеет ступенчатый вид;
все опорные элементы равны единице;
над опорными элементами всюду выше стоят только нули.
Поскольку в некоторых доказательствах мы собираемся использовать принцип математической индукции, то приведем его формулировку.
Принцип математической индукции. Пусть сформулировано некоторое утверждение, зависящее от натурального числа n. Тогда, доказав что
это утверждение верно для некоторого начального
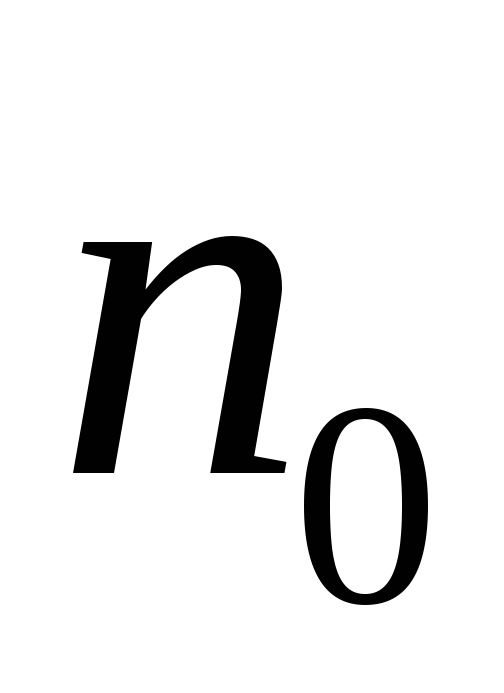 (доказавбазу
индукции);
(доказавбазу
индукции);это утверждение верно для
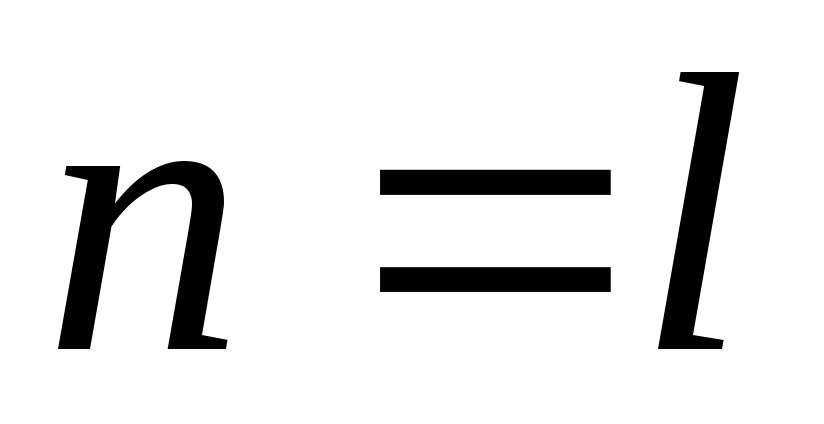 ,
предполагая, что утверждение верно для
всех
,
предполагая, что утверждение верно для
всех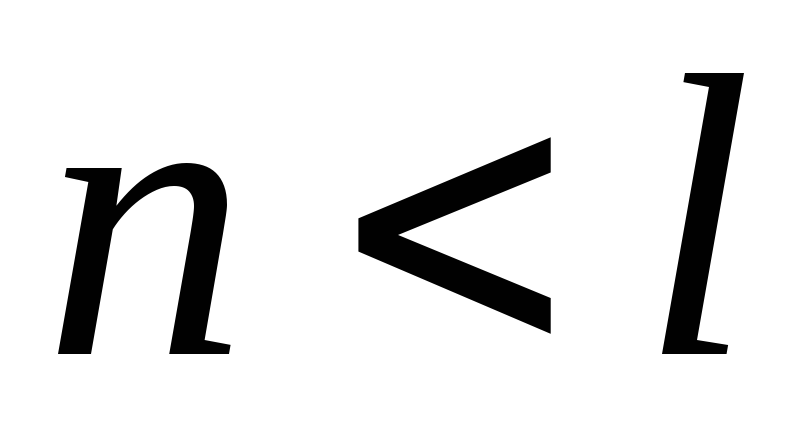 (доказавшаг
индукции, принимая индуктивное
предположение);
(доказавшаг
индукции, принимая индуктивное
предположение);
можно сделать вывод, что данное утверждение верно для любого натурального n.
Теорема. Любая матрица А может быть приведена к ступенчатой матрице с помощью элементарных преобразований строк первого и второго типов.
Доказательство.
Проведем
доказательство
индукцией
по числу строк матрицы. Если имеется
всего одна строка, то матрица А
уже ступенчатая. Пусть теперь матрица
А
содержит m
строк, где
![]() .
Предположим, что матрицу с числом строк,
меньшимm,
можно привести к ступенчатому виду.
Если матрица А
нулевая, то она ступенчатая. Если А
ненулевая, то в ней есть хоть один
ненулевой элемент. Ненулевой элемент
располагается в какой-то строке. Значит,
в матрице А
есть ненулевые строки. Выберем ту строку,
в которой опорный элемент располагается
в столбце с наименьшим номером, скажем
с номером
.
Предположим, что матрицу с числом строк,
меньшимm,
можно привести к ступенчатому виду.
Если матрица А
нулевая, то она ступенчатая. Если А
ненулевая, то в ней есть хоть один
ненулевой элемент. Ненулевой элемент
располагается в какой-то строке. Значит,
в матрице А
есть ненулевые строки. Выберем ту строку,
в которой опорный элемент располагается
в столбце с наименьшим номером, скажем
с номером
![]() .
Применив преобразование первого типа,
перенесем эту строку на первое место.
Тогда матрица примет вид:
.
Применив преобразование первого типа,
перенесем эту строку на первое место.
Тогда матрица примет вид:
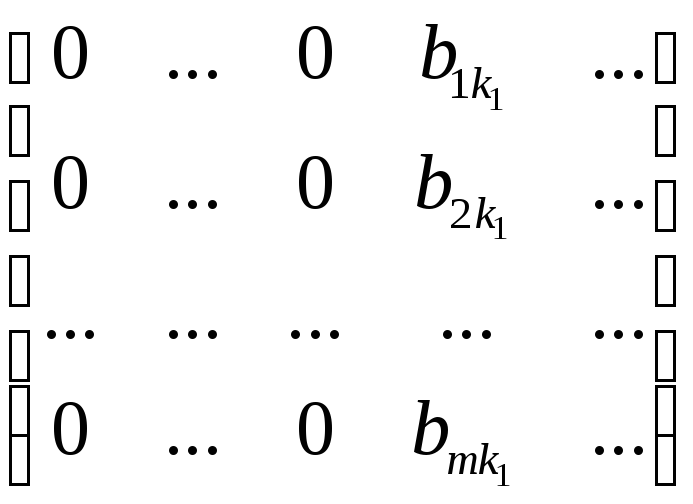 ,
,
причем
![]() .
Теперь будем применять преобразования
второго типа: ко второй строке прибавим
первую, умноженную на
.
Теперь будем применять преобразования
второго типа: ко второй строке прибавим
первую, умноженную на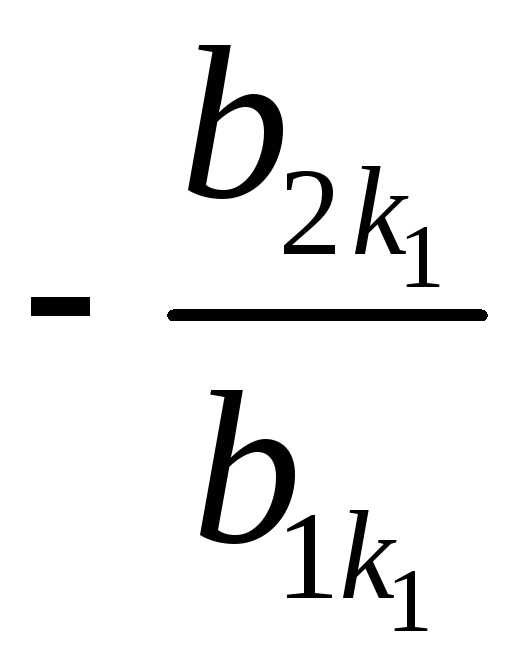 ,
к третьей строке – первую, умноженную
на
,
к третьей строке – первую, умноженную
на![]() ,
и т. д. После применения
,
и т. д. После применения![]() таких элементарных преобразований
добьемся того, что в
таких элементарных преобразований
добьемся того, что в![]() столбце всюду, кроме первой строки,
будут нули:
столбце всюду, кроме первой строки,
будут нули:
 .
.
