Лекции - 2005 / lecture_12_1

(С) ИиКМ РХТУ сентябрь 2003г. Калинкин Владимир Николаевич		1
Методы многомерной оптимизации.
Дана некоторая функция многих переменных f(x1,x2,x3,…..,xn) или		→
		f ( x) надо найти такое
→	→
значение x * , при котором функция	f (x* ) принимает экстремальное значение (минимальное или

→→

*x

максимальное). Некоторая функция f ( x) в точке		имеет минимум, если в любой сколь угодно
	→	→	→
малой окрестности точки x * выполняется условие		f ( x) > f (x* ) и максимум, если выполняется
→	→
условие f ( x) < f (x* ) .

→

Процесс поиска экстремального значения иногда называют оптимизацией. Функцию f ( x)

→

называют оптимизируемой или целевой функцией, а вектор x оптимизируемые параметры или параметры оптимизации. В области определения функции может быть несколько экстремумов. В этом случае все экстремальные значения называются локальными экстремумами, а наибольшие или наименьшие значения из всех локальных называются глобальными экстремумами. Перед использованием метода оптимизации необходимо чтобы было известно:

→

1) вид функции f ( x) ;

2) границы поиска по каждой переменной [a1;b1], [a2;b2],…..,[an;bn] либо, вместо границ,

				(0)
			x1
может быть задана начальная точка поиска экстремума x		(0)	x2(0)			;
			=
			.....
				(0)
3)	точность поиска экстремума.		xn

Все существующие методы многомерной оптимизации позволяют определить лишь один из локальных экстремумов.

Какой именно локальный экстремум будет определён, зависит от выбора начального приближения.

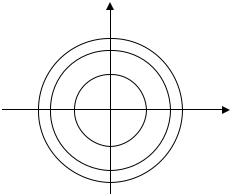
Все методы поиска экстремума будем рассматривать относительно случая поиска минимума, для функции двух переменных. Для удобства графической иллюстрации методов определим представление функции в виде линий уровня.

f(x1,x2)

x1

x2

уровням.

→

Дана целевая функция f ( x) = x12 + x22 , которая графически

представляет собой поверхность параболоида вращения.

Проведем сечения поверхности равно отстоящими плоскостями, которые параллельны плоскости изменения переменных x1 и x2.

Линии этих сечений проецируем на плоскость изменения переменных. Получим концентрические окружности. Эти линии называются линиями уровня или линиями постоянных значений. Основная характеристика любой из линий это то, что в любой точке этой линии значение функции постоянно.

Рассечем заданную поверхность функции тремя плоскостями по

y = x2		+ x2	=1	y	2	= x2	+ x2	= 2	y	3	= x2	+ x2	= 3
1	1	2				1	2				1	2

Тогда линии уровня будут подставлять окружности с соответствующими радиусами

R1=√1=1

R2=√2=1.4

R3=√3=1.73

(С) ИиКМ РХТУ сентябрь 2003г. Калинкин Владимир Николаевич

2

x2

x1

Все методы многомерной оптимизации делятся на два класса:

1)Градиентные

2)Безградиентные

Градиентом называется вектор равный сумме произведений частных производных на соответствующие орты. Орта - единичные связанный вектор направленный вдоль координатной

1

0

0

→

0

→

1

→

0

оси. e

1 =

e

2 =

……….. e n =

.

.

.

0

0

1

→

→

∂f

→

∂f

→

∂f

→

grad ( f ( x)) =

e1 +

e 2

+......... +

e n

∂x

∂x

∂x

2

n

1

∂f

→

→

∂f

1

∂f

0

∂x1

Для случая функции двух переменных grad ( f ( x)) =

=

+

∂x1

∂x2

0

1

∂f

∂x2

Основные свойства градиента:

1)Норма градиента определяет скорость изменения функции в направление градиента.

2)Градиент всегда направлен в сторону наиболее быстрого возрастания функции, т.е. в этом направлении норма вектора градиента максимальна.

Антиградиентом называется вектор, направленный в противоположную сторону. Пример:

дана функция

→

+ x2

→

=

1

f ( x) = x2

. Вычислить вектор градиент в точке x

1

2

2

∂f

2x

2

→

→

∂x

grad ( f ( x)) =

=

1

=

1

∂f

2x2

4

∂x2

Градиентный метод.

→

1.Дана функция n переменных f ( x) . Также заданы точность ε, величина параметра

→(0)

шага h и точка начального приближения x расположенная в области поиска экстремума.

(С) ИиКМ РХТУ сентябрь 2003г. Калинкин Владимир Николаевич

3

2.За текущее значение вектора приближения принимаем начальное приближение

→

→(0)

→

x

= x

и вычисляем значение функции в этой точке FX= f ( x)

∂f

∂x

1

→

∂f

∂f

3.

Вычисляем вектор градиента G =

=

∂x2

единичный вектор градиента

→

∂ x

...

∂f

∂x

n

→

→1

G

V =

→

|| G ||

4.

→

→

→

Делаем шаг в направление антиградиента z

= x

−h V и вычисляем значение

→→

функции в точке z FZ= f ( z)

5.	Проверяем условие FZ < FX. Если условие выполняется, то за текущее приближение
→	→	→
принимаем		= z , FX=FZ и переходим на пункт 3.
6.		→
	Иначе, проверяем условие окончания h < ε, если оно выполняется, то выводим x и

FX.

7.Если не выполняется, то уменьшаем параметр шага h=h/3 и переходим на пункт 3.

начало

→(0)

, h, ε

||

→

x

f ( x)

→

→(0)

→

x

= x ; FX= f ( x)

→

∂f

→

1

→

G =

;

V =

G

→

→

∂ x

|| G ||

→

=

→

→

→

z

x

−h V ; FZ+ f ( z)

FZ<FX

| h | ≤ ε

→

, FX

x

h:=h/3

конец