Лекции - 2005 / lecture_4-5

(С) ИиКМ РХТУ февраль 2004г. Калинкин Владимир Николаевич

1

Лекция -(4,5)

Вектора, матрицы и программирование операций над ними.

С упорядоченной последовательностью действительных чисел a1,a2,a3,…..an-1,an можно связать

→

понятие связанного вектора в n-мерном пространстве и обозначить как a =[a]

a1a2 = ..an

или понятие точки A(a1,a2,a3,….an). Числа a1,a2,a3,…an называются координатами точки A

→

или компонентами вектора a , а количество компонент в векторе называется размерностью этого вектора.

Характеристики и типы векторов

Норма (длина) вектора

→

=

n

→

2

→

= 22 +32 = 3.61 пример

a

∑ai2

a

=

a

i=1

3

программы: Option base Option explicit Sub norma_m()

Dim n%,a!(),s!,i%

n=cells(2,1): Redim a(n): for i=1 to n: a(i)=cells(i+3,1): next i: s=0 For i=1 to: s=s+a(i)*a(i): next i

s=sqr(s): cells(2,3)=s End Sub

Вектор считается равным нулю, если все его компоненты равны нулю и обозначается

	0
→	0
как 0 =
	.
	.
	0
		→	0.6					→				=1
Единичный вектор – это вектор, длина которого равна единице. a			=					a
			0.8

Два вектора с одинаковой размерностью равны тогда, когда равны их соответствующие

→	→
компоненты. a	= b a1	= b1 , a2	= b2 ,....., an = bn где i =1,2,3,..., n

Операции над векторами.

Сложение и вычитание векторов. Складывать или вычитать можно только вектора с одинаковой размерностью. Результатом операции сложения (вычитания) является вектор, компоненты которого равны сумме (разности) соответствующих компонент двух других векторов.

→ → →

+bi

где i =

→

3 →

2

→

=

3

2

5

c = a+ b ci = ai

1,2,3,.., n a

= b

=

c

+

=

5

7

5

7

12

→

→

→

→

свойство операции сложения (вычитания): коммутативность a

+ b

= b

+ a

→

→

→

→

→ →

ассоциативность a

+(b

+ c) = (a

+ b) + c

(С) ИиКМ РХТУ февраль 2004г. Калинкин Владимир Николаевич

2

For i=1 to n: c(i)=a(i)+b(i): next i

Умножение вектора на константу. Результатом умножения является вектор, компоненты которого равны произведению соответствующих компонент исходного вектора на константу.

→

→

гдеi =1,2,3,..., n

→

2

→

= 2.3

2

4.6

c = λ

a ci =λ ai

λ = 2.3 a

=

3

c

3

=

6.9

Свойства операции:

→

→

→

→

→

→

→

λ (β

→

→

λ (a

+ b) =

λ a+λ

b (λ + β) a

= λ a

+ β a

a) = (λ

β) a

→

→

→

→

→

→

0 a = 0 1

a

= a (−1) a

= −a

Транспонирование вектора – это изменения представления вектора. Представление в виде столбца на строку.

	a
	1
→	a2		→
a =			a	T
	.
	.
	an

= [a a . . . . a a			] a	=	2 aT	= [2 3]
			→		→
1 2	n−1	n
					3

Скалярное произведение векторов – это значение суммы произведений соответствующих компонент двух векторов.

→ →

→

→

n

bi

где i =1,2,3,..., n

→

=

2

→

4

z = [23]

4

= 2 4 +3

5

= 23

z = (a, b) = aT b

= ∑ai

a

b

=

i=1

3

5

5

s = 0

For i=1 to n: s=s+a(i)*b(i): next i

Scal=sqr(s)

→

→

Угол между векторами. Косинус угла cos(θ) =

aT b

→

→

a

b

→

→

= 0

Ортогональность векторов cos(θ) = 0 т.е.aT b

Могут возникнуть две задачи:

Проверка ортогональности двух векторов даны вектора

→

−1

→

1

z = [−1 3

1

3 3 −2 4 = 0

a

=

3

b =

3

−2] 3 = −1 1 +

−2

4

4

Эти вектора ортогональны.

Найти вектор ортогональный данному.

→

−1

b1

=

3

[−1 3 −2] b

=(−1) b +3 b +(−2) b

=0

задаем b =3 b

=5 получаем

a

2

1

2

3

1

2

−2

b3

→

3

=

(−3) +15 +(−2) b3 = 0 12 −2 b3 = 0 b3 = 6 b

5

6

(С) ИиКМ РХТУ февраль 2004г. Калинкин Владимир Николаевич

3

Линейная зависимость векторов

→									m	→
Вектора a(i) называются линейно зависимыми, если соотношение ∑βi a(i) = 0
								i=1
справедливо,		хотя бы при одном множителе βi			отличным от нуля.
Пример:
2		1		β1 a(1) + β2 a(2) = 0	2	1		=	0
a(1) = ;	a(2) =				β1 + β2
4		2			4	2			0

β1 2 + β2 1 = 0 β2 = −2 β1

β1 4

+ β2 2 = 0

β1 4 − β1 4 = 0 β1 0 = 0 при любом β1

a(1)

1

+ 2

β1 a(1)

+ β

1

+ 2

0

=

; a(2) =

2

a(2) = 0 β1

+ β2

=

2

−1

2

−1

0

β1 1 + β2 2 = 0 β1 = −2 β2

β2 (−5) = 0 только при β2

β1 2

− β2 1 = 0

− β2 4 − β2 1 = 0

= 0

Если m>n, то вектора линейно зависимы, где m - количество векторов, а n – размерностью пространства.

матрицы и программирование операций над нами.

совокупность чисел расположенных в прямоугольной таблицы, состоящей из n строк и m столбцов, называется матрицей и обозначается как:

=	a	a	a			a
	11	12	13			1m
A =[A]= a21		a22	a23	a2m
		an2	an3
	an1					anm

положение элемента aij в таблице определяется двумя индексами i и j, где i определяет номер строки (1 ≤i ≤ n) , а j столбца (1 ≤ j ≤ m) .

типы матриц

Матрица состоящая из одной строки – называется вектор строка n=1 Матрица состоящая из одного столбца - называется вектор столбец m=1 Если n равно m матрица называется квадратной

Верхне треугольная aij=0 при i>j Нижне треугольная aij=0 при i<j

Диагональная	aij	= 0 при i ≠ j
Единичная aij	= 1 при i = j
	0 при i ≠ j
		=	=
Равенство матриц		A =	B т.е. aij=bij где i=1,2,3,…,n	j=1,2,3,…,m

Характеристики матриц

Норма является некоторой обобщенной оценкой матрицы. Существуют следующие выражения для вычисления норм:

=		n	m
A	=	∑∑ai2, j каноническая (Эвклидова)
	1	i=1	j=1

(С) ИиКМ РХТУ февраль 2004г. Калинкин Владимир Николаевич

4

=

m

ai, j

i =1,2,3, …., n

A

= max ∑

i

j=1

=

n

ai, j

j=1,2,3, …., m

A

= max ∑

j

i=1

a11

a12

...

a1m

определитель detA= a

a21

a22

...

a2m

... ... ... ...

an1

an2

...

anm

Операции над матрицами

Транспонирование матрицы

=T

a

a

21

a

31

a

n1

11

A

=[A]T = a12

a22

a32

an2

a2m a3m

a1m

anm

Сложение и вычитание

=

=

=

C

= A ± B ;

cij = aij

+bij , где i=1,2,3,…..,n j=1,2,3,…,m

свойства: коммутативность

=

=

=

+

=

A

+ B

= B

A ; ассоциативность

=

=

=

=

=

=

A +( B

+ C ) =( A + B ) + C

for i=1 to n for j=1 to m

c(i,j)=a(i,j)+b(i,j) next j

next i

Умножение матрицы на константу

=	=				j=1,2,3,…,m
C = β A ; cij=β*aij , где i=1,2,3,…..,n
	=	=	=		=	=	=	=
свойства: β ( A		+ B ) = β * A		+ β * B ;		(α + β) * A	=α * A	+ β * A ;

==

β*(α * A ) = (β *α)* A

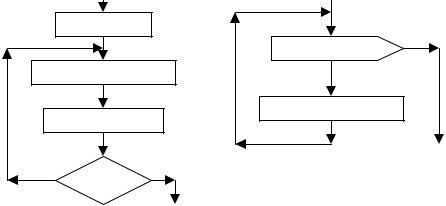
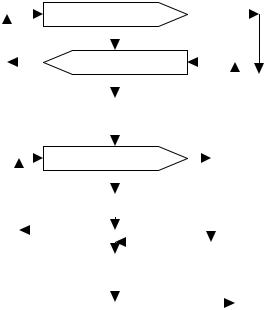
Способ записи циклического алгоритма с использованием параметра цикла

i:=1

i=1 шаг 1 до n

группа операторов

группа операторов

i:= i+1

i<=n

(С) ИиКМ РХТУ февраль 2004г. Калинкин Владимир Николаевич

5

Умножение матриц

=

=

=

=

=

C = A* B ≠

B * A

=

=

=

; ограничения накладываемые на матрицы:

C nm =

A nk * B km

Количество столбцов матрицы

=

=

A должно равняться количеству строк матрицы B .

=

Элемент cij

вычисляется как скалярное произведение i строки матрицы A и j столбца

=

матрицы B

k

i=1 шаг 1 до n

cij

= ∑ail *blj

фрагмент программы

l=1

for i=1 to n

j=1 шаг 1 до m

for j=1 to m

s=0

for l=1 to k

s:=0

s=s+a(i,l)*b(l,j)

next l

l=1 шаг 1 до k

c(i,j)=s

next j

next I

s:=s+ail*blj

2 1 0

1

0

1

2

=

5 1

2 5

C

= 1

2

1

* 3

1

0

1 = 8 4

2 6

cij:=s

1

2

1

2

=

Обратной матрицей называется квадратная матрица размерностью n на n - Ann−1 . Результатом умножение обратной матрицы на исходную, как справа, так и слева

=	=	= =	=
является единичная матрица. A	−1* A	= A* A	−1= E

Метод Гаусса-Жордана.

Алгоритм.

Строим расширенную матрицу, дописав к исходной матрице справа единичную

	=		=			преобразуем расширенную так, чтобы на месте исходной получилась
	A		E	n n
	n n

единичная, то на месте единичной получится обратная		=		=
	En n			Ann−1

(С) ИиКМ РХТУ февраль 2004г. Калинкин Владимир Николаевич								6
=			справа к
1. Строим расширенную матрицу С размерностью n на 2*n, как исходная,
=			=		=			.
которой дописывается единичная матрица той же размерности. C n 2n =		A			E	n n
			n n

Задаем номеру ведущей строки k=1

2. Все элементы k-ой строки делим на элемент ckk, т.е. ckj = ckj ; j=k, k+1, k+2,

ckk

k+3,….,2*n; т.е. ckk=1

3. Преобразуем все строки кроме k–ой, i=1,2,3,….,n i≠k так, чтобы элементы cik=0. Для этого из из каждого элемента i-ой строки вычитаем соответствующие элемент k-ой строки умноженные на элемент cik, т.е. cij=cij-ckj*cik ; j= k, k+1,k+2,….., 2*n

4.Проверяем, если k<n, то k=k+1 выполняем пункт 2, иначе выводим полученную обратную матрицу, расположенную на месте единичной.

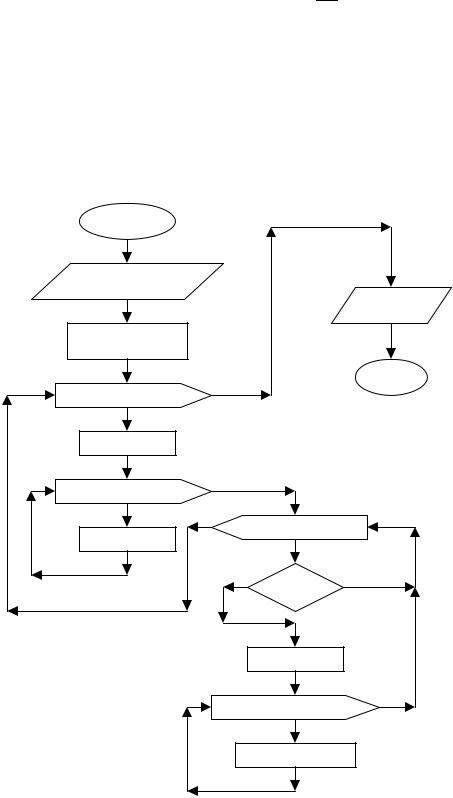
начало

ввод n,[A]

Вывод

[C]

формирование

матрицы [C]

конец

k=1 шаг 1 до n

s:=ckk

j=k шаг 1 до 2n

i=1 шаг 1 до n

ckj:=ckj/s

i=k

s:=cik

j=k шаг 1 до 2n cij=cij-s*ckj

(С) ИиКМ РХТУ февраль 2004г. Калинкин Владимир Николаевич

7

Option Explicit

Option Base 1

Sub GausGord()

Dim a!(3, 3), b!(3, 3), c!(3, 6) Dim i%, j%, k%, n%, s!

n = Cells(1, 1)

For i = 1 To n: For j = 1 To n: a(i, j) = Cells(i + 1, j): Next j: Next i For i = 1 To n: For j = 1 To 2 * n

If j > n Then

If i = j - n Then c(i, j) = 1 Else c(i, j) = 0 Else

c(i, j) = a(i, j) End If

Next j: Next i For k = 1 To n

s = c(k, k): For j = k To 2 * n: c(k, j) = c(k, j) / s: Next j For i = 1 To n

If i <> k Then s = c(i, k)

For j = k To 2 * n: c(i, j) = c(i, j) - c(k, j) * s: Next j End If

Next i

Next k

For i = 1 To n: For j = 1 To 2 * n: Cells(i + 1, j + n + 1) = c(i, j): Next j: Next i End Sub

Пример решения.

	2,00	1,00	1,00			2,00	1,00	1,00		1,00	0,00	0,00		k=1
[A] =	1,00	2,00	1,00		[C] =	1,00	2,00	1,00		0,00	1,00	0,00
	1,00	1,00	2,00			1,00	1,00	2,00		0,00	0,00	1,00
1,00	0,50	0,50		0,00	0,00		i=2,3		1,00	0,50	0,50		0,50	0,00	0,00		k=2
			0,50
1,00	2,00	1,00	0,00	1,00	0,00	1,00			0,00	1,50	0,50		-0,50	1,00	0,00
1,00	1,00	2,00	0,00	0,00	1,00	1,00			0,00	0,50	1,50		-0,50	0,00	1,00
1,00	0,50	0,50		0,00	0,00		i=1,3			0,00	0,33			-0,33	0,00		k=3
			0,50			0,50			1,00				0,67
0,00	1,00	0,33	-0,33	0,67	0,00				0,00	1,00	0,33		-0,33	0,67	0,00
0,00	0,50	1,50	-0,50	0,00	1,00	0,50			0,00	0,00	1,33		-0,33 -0,33 1,00
1,00	0,00	0,33		-0,33	0,00		i=1,2			0,00	0,00			-0,25 -0,25
			0,67			0,33			1,00				0,75
0,00	1,00	0,33	-0,33	0,67	0,00	0,33			0,00	1,00	0,00		-0,25	0,75	-0,25
0,00	0,00	1,00	-0,25 -0,25		0,75				0,00	0,00	1,00		-0,25 -0,25		0,75