ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

Г. Д. Гефан, Н.К. Ширяева

ВЕРОЯТНОСТЬ, СЛУЧАЙНЫЕ ПРОЦЕССЫ, МАТЕМАТИЧЕСКАЯ СТАТИСТИКА:

ЭЛЕМЕНТЫ ТЕОРИИ И КОМПЬЮТЕРНОГО МОДЕЛИРОВАНИЯ

УЧЕБНОЕ ПОСОБИЕ

для подготовки бакалавров по направлениям «Информационные системы», «Информационная безопасность», «Программная инженерия», «Мехатроника и робототехника», «Экономика»,

«Управление качеством»

ИРКУТСК

2013

УДК 519. 2 ББК 22. 17 Г 45

Рецензенты:

О.В. Кузьмин, д. ф.-м.н., профессор, зав. кафедрой дискретной математики и теории вероятностей ИГУ; Л.В. Аршинский, д. т. н., профессор, зав. кафедрой «Информационные системы» ИРГУПС.

Гефан Г.Д. , Ширяева Н.К.

Г45 Вероятность, случайные процессы, математическая статистика: элементы теории и компьютерного моделирования. Учебное пособие. – Иркутск: Ир-

ГУПС, 2013. – 132 с.

Главным элементом содержательной новизны пособия является лабораторный компьютерный практикум, состоящий из 9 работ, выполняемых с помощью табличного процессора Excel или пакета Mathcad. Описание каждой работы содержит все необходимые теоретические сведения и практические примеры.

Библиогр.: 20 назв.

©Гефан Г.Д., Ширяева Н.К. 2013

©Иркутский государственный университет путей сообщения, 2013

2

О Г Л А В Л Е Н И Е

ПРЕДИСЛОВИЕ……………………………………………………………… 5

РАБОТА 1.

СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ СОБЫТИЙ НА

ОСНОВЕ ПРЕДСТАВЛЕНИЙ ОБ ЭЛЕМЕНТАРНЫХ ИСХОДАХ.

Понятие метода Монте-Карло. Статистическая проверка классического определения вероятности………………………………………………… 7

РАБОТА 2.

СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ СОБЫТИЙ И

ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
Метод Монте-Карло: три вида единичного жребия и их реализация. Стати-
стическая проверка законов алгебры событий. Моделирование дискретной
случайной	величины с произвольным законом		распределе-
ния...........……………………………………………………………...				25
РАБОТА 3.
ЧИСЛЕННОЕ	МОДЕЛИРОВАНИЕ	ХАРАКТЕРИСТИК	СИСТЕМЫ
ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
Оценивание числовых характеристик случайных величин, параметров				38
функций регрессии и коэффициента корреляции………………………………
РАБОТА 4.
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА.
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ЛАПЛАСА
Число наступлений события в серии однородных независимых опытов: раз-
личные подходы. Проверка центральной предельной теоремы. Проверка
теорем Лапласа. Разыгрывание нормальной случайной величины методом
Монте-
Карло.……………………………………………...............................				46
РАБОТА 5.
СЛУЧАЙНЫЕ ПРОЦЕССЫ С ДИСКРЕТНЫМИ СОСТОЯНИЯМИ И
ДИСКРЕТНЫМ ВРЕМЕНЕМ
Решение задач с использованием матрицы переходных вероятностей. Мо-
делирование переходов в цепи Маркова. Статистическое моделирование
процесса с дискретным временем……………………………………				60
РАБОТА 6.
СЛУЧАЙНЫЕ ПРОЦЕССЫ С ДИСКРЕТНЫМИ СОСТОЯНИЯМИ И
НЕПРЕРЫВНЫМ ВРЕМЕНЕМ
Решение задач с использованием матрицы интенсивностей. Численное мо-
делирование динамики распределения вероятностей состояний. Статисти-
ческое моделирование процесса с непрерывным временем………………..				78
РАБОТА 7.				91

3

СТАТИСТИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ КОЛИЧЕСТВЕННОГО ПРИЗНАКА.
ТОЧЕЧНОЕ И ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ ГЕНЕРАЛЬНЫХ
ХАРАКТЕРИСТИК ПО ВЫБОРОЧНЫМ ДАННЫМ
Гистограмма частот. Свойства точечных оценок. Построение доверительно-
го интервала для оценки математического ожидания случайной величи-
ны………………………………………………………………………
РАБОТА 8.
ВЫРАВНИВАНИЕ СТАТИСТИЧЕСКОГО РЯДА.
ПРОВЕРКА ГИПОТЕЗЫ О ТИПЕ РАСПРЕДЕЛЕНИЯ.
Теоретические частоты предполагаемого нормального распределения.
Критерий Пирсона………………………………………………………….……	107
РАБОТА 9
КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ
Выборочный коэффициент линейной корреляции. Применение метода наи-
меньших квадратов в регрессионном анализе данных………………………….	115
БИБЛИОГРАФИЧЕСКИЙ СПИСОК............................................................	124
ПРИЛОЖЕНИЕ 1. ТАБЛИЦА ЗНАЧЕНИЙ ФУНКЦИИ ГАУССА ………………….	125
ПРИЛОЖЕНИЕ 2. ТАБЛИЦА ЗНАЧЕНИЙ ФУНКЦИИ ЛАПЛАСА ……………...	126
ПРИЛОЖЕНИЕ 3. КОЭФФИЦИЕНТЫ СТЬЮДЕНТА t(γ,n) ......……………..	127
ПРИЛОЖЕНИЕ 4. КРИТИЧЕСКИЕ ТОЧКИ РАСПРЕДЕЛЕНИЯ χ2 ......………..	128
ПРИЛОЖЕНИЕ 5. КРИТИЧЕСКИЕ ТОЧКИ РАСПРЕДЕЛЕНИЯ
СТЬЮДЕНТА................................................................................................	129
ПРИЛОЖЕНИЕ 6. СООТВЕТСТВИЕ НЕКОТОРЫХ СТАТИСТИЧЕСКИХ
ФУНКЦИЙ ПАКЕТОВ EXCEL И CALC……………………………………….	130

4

Предисловие

Теорию вероятностей и математическую статистику принято относить к разделам прикладной математики, поскольку они явно сориентированы на применение математических методов, моделей, алгоритмов в других областях науки и практики.

Преподавание теории вероятностей и математической статистики в высшей школе выглядит стройным и последовательным, но, на наш взгляд, имеет и некоторые традиционные недостатки.

1.Обособление теории вероятностей от идей и подходов математической статистики. Хотя теория вероятностей просто «пропитана духом» статистического опыта, преподаётся она, как правило, не вместе с математической статистикой, а до неё. В такой последовательности, конечно, есть своя логика, но отрицательный эффект тоже достаточно заметен – отрыв теории вероятностей от практики, иногда превращение её в абстрактную науку.

2.Чрезмерное увлечение классической схемой теории вероятностей и комбинаторными методами в ущерб собственно вероятностным понятиям. По нашему мнению, введение элементов комбинаторики должно быть подчинено вероятностным задачам, а не наоборот.

3.Неоправданно высокий математический формализм, затрудняющий восприятие сути даже таких простых понятий, как случайная величина и ее числовые характеристики.

4.Слабое использование современных вычислительных средств. Изучать теорию вероятностей и математическую статистику только с помощью бумаги, ручки и примитивного калькулятора – неэффективно, неинтересно, несовременно (а преподавать – тем более).

Предлагаемое пособие представляет собой попытку преодолеть перечисленные недостатки. Не отрицая необходимости традиционных форм занятий – лекций и семинаров, мы считаем нужным активно использовать для обучения компьютер на лабораторных практикумах. Первая причина буквально лежит на поверхности и очевидна для всех: даже общедоступный табличный процессор Excel позволяет провести необходимые статистические вычисления в доли секунды, практически независимо от объема имеющихся данных. Также компьютер способен облегчить и решение многих задач по теории вероятностей, например, с применением формул Бернулли, Пуассона, теорем Лапласа и т.д. С помощью графических средств можно ярко иллюстрировать законы распределения случайных величин. Но ещё эффективнее и интереснее выглядит применение компьютера для моделирования случайных событий, величин, процессов методом статистических испытаний (методом Монте-Карло). Например, с помощью компьютера можно показывать, каким образом статистическая частота сближается с вероятностью при увеличении числа экспериментов. Еще не посвятив студентов в тонкости и точные формулировки закона больших чисел, преподаватель при правильном применении компьютерного моделирования может сформировать у аудитории верное представление о том, что относитель-

5

ная частота события при большом числе экспериментов, скорее всего, «близка» к его вероятности. Таким образом, довольно абстрактное понятие вероятности события получает наглядное содержание, отрыв теории вероятностей от статистики преодолевается на первых же занятиях.

Лабораторный практикум (18 часов учебных занятий) поддерживается курсом лекций и семинарских занятий. Теоретические сведения и практические примеры, необходимые для понимания сути выполняемых лабораторных работ, включены в их описания. Работы выполняются студентами с помощью офисной программы Excel и/или с помощью пакета Mathcad.

Предполагается, что на занятии группа студентов, работающих на персональных компьютерах, выполняет одно и то же задание под руководством преподавателя, а во время защиты работ (на следующих занятиях) каждый студент получает индивидуальные вопросы и небольшие дополнительные задания. Каждое описание лабораторной работы включает в себя:

1)время для выполнения и защиты работы;

2)цель работы;

3)необходимые сведения из теории и практики;

4)задание для работы (иногда несколько заданий);

5)инструкции по выполнению задания;

6)контрольные вопросы.

Наш опыт преподавания говорит о том, что практикумы, включающие в себя численное экспериментирование, воспринимаются студентами с большим интересом, освобождают их от некоторых шаблонных умозрительных представлений и способствуют появлению навыков самостоятельного научного исследования.

Авторы благодарны профессору О.В. Кузьмину, профессору Л.В. Аршинскому и доценту А.В. Димову за полезные замечания и советы.

6

Работа 1

СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ СОБЫТИЙ НА ОСНОВЕ ПРЕДСТАВЛЕНИЙ ОБ ЭЛЕМЕНТАРНЫХ ИСХОДАХ.

Понятие метода Монте-Карло. Статистическая проверка классического определения вероятности

Время на выполнение и защиту – 3 часа

Цель работы:

1)уяснение сути классического определения вероятности;

2)получение практического опыта по применению теоремы Бернулли (статистического определения вероятности);

3)знакомство с применением метода Монте-Карло к решению вероятностных задач;

4)изучение ряда функций Excel и Mathcad.

Понятие вероятности

Вероятность события — это количественная мера возможности того, что некоторый факт (событие) осуществится при определённых условиях опыта.

Невозможным называется такое событие Aневозм, наступление которого в

данном опыте абсолютно исключено. Условно принимается, что его вероят-

ность P(Aневозм) = 0 .

Достоверным называется событие Aдост , которое обязательно должно

произойти при проведении опыта. Условно принимается, что его вероятность

P(Aдост) =1.

Например, появление трёх ‘‘орлов’’ при бросании двух монет – невозможное событие. Появление от одного до шести очков при бросании игральной кости – достоверное событие.

Событие A, не являющееся ни невозможным, ни достоверным (оно может либо наступить, либо нет), будем называть случайным.

Вероятности событий ограничены неравенством 0 ≤ P(A) ≤1. «Границы»

этого неравенства соответствуют невозможному и достоверному событиям, а вероятности случайных событий лежат внутри интервала (0, 1).

Классическое определение вероятности

Пусть всего имеется n равновозможных элементарных исходов некоторого опыта, m из которых ведут к наступлению события A (иначе говоря, благоприятствуют этому событию). Тогда вероятность события A равна:

7

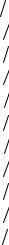
P(A) =	m	.	(1.1)
	n

Подчеркнём, что классическое определение вероятности применимо только тогда, когда различные исходы опыта обладают симметрией и поэтому одинаково возможны.

Пример 1. При бросании одной игральной кости имеется шесть равновозможных исходов: «1», «2», «3», «4», «5» и «6». Вероятность каждого из этих исходов равна 1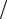6 .

Пример 2. При бросании двух игральных костей сумма выпавших очков может составить от 2 до 12. Однако соответствующие события «2», «3», «4», …, «12» не являются равновозможными. Рассмотрим, какие элементарные исходы благоприятствуют этим событиям, и найдём соответствующие вероятности (табл. 1.1). Элементарными исходами считаем любые возможные комбинации очков на двух брошенных костях (всего таких комбинаций существует 6 ×6 = 36 , поскольку каждый возможный результат бросания первой кости может сопровождаться любым возможным результатом бросания второй кости). Необходимо различать исходы с внешне одинаковым набором выпавших очков, но реализующиеся различным способом с учётом наличия двух разных

Табл. 1.1. Бросание двух игральных костей

Сумма очков на	Благоприятные исходы	Число бла-	Вероятность со-
двух костях		гоприятных	бытия
(событие)		исходов
2	1+1	1	1 36
3	1+2, 2+1	2	2 36
4	1+3, 3+1, 2+2	3	3 36
5	1+4, 4+1, 2+3, 3+2	4	4 36
6	1+5, 5+1, 2+4, 4+2, 3+3	5	5 36
7	1+6, 6+1, 2+5, 5+2, 3+4, 4+3	6	6 36
8	2+6, 6+2, 3+5, 5+3, 4+4	5	5 36
9	3+6, 6+3, 4+5, 5+4	4	4 36
10	4+6, 6+4, 5+5	3	3 36
11	5+6, 6+5	2	2 36
12	6+6	1	1 36
		Всего 36	В сумме 1

костей. (Например, чтобы понять, что 1+2 и 2+1 есть разные исходы, достаточно представить себе, что первая кость – красного цвета, а вторая – жёлтого, и

т.д.)

8

Пример 3. При бросании трёх игральных костей сумма выпавших очков может составить от 3 до 18, и эти события, конечно, не являются равновозможными. Нахождение соответствующих вероятностей – значительно более сложная задача, чем в примере 2. Её решение представлено в табл. 1.2.

Табл. 1.2. Бросание трёх игральных костей

	Сумма оч-		Число	Вероят-
			благо-
	ков на трёх
		Благоприятные исходы	прият-	ность
	костях (со-
			ных ис-	события
	бытие)
			ходов
	3	1+1+1	1	1 216
	4	1+1+2, 1+2+1, 2+1+1	3	3 216
	5	1+1+3, 1+3+1, 3+1+1,	6	6 216
		2+2+1, 2+1+2, 1+2+2
		1+1+4, 1+4+1, 4+1+1,		10 216
	6	3+2+1, 3+1+2, 2+1+3, 2+3+1, 1+2+3, 1+3+2,	10
		2+2+2
	…	…	…	…
		5+4+1, 5+1+4, 4+5+1, 4+1+5, 1+5+4, 1+4+5,
		5+3+2, 5+2+3, 3+5+2, 3+2+5, 2+3+5, 2+5+3,
	10	6+3+1, 6+1+3, 3+1+6, 3+6+1, 1+6+3, 1+3+6,	27	27 216
		6+2+2, 2+6+2, 2+2+6,
		4+4+2, 4+2+4, 2+4+4,
		4+3+3, 3+4+3, 3+3+4
	11	…	27	27 216
	…	…	…	…
	18	6+6+6	1	1 216
			Всего	В сумме
			216	1

Табл. 1.2 заполнена лишь частично, чтобы читатель имел возможность закончить расчёты самостоятельно и убедиться, что полное число элементарных исходов равно 216, а сумма вероятностей равна 1. Поясним подсчёт числа благоприятных исходов. Набору, в котором присутствует 3 разных цифры, будет соответствовать 6 элементарных исходов (число перестановок из 3 элементов равно 6). Набору, в котором 2 цифры одинаковы, а третья отличается от них, будет соответствовать 3 элементарных исхода (число перестановок из 3 элементов с повторением 2 элементов, либо число сочетаний из 3 элементов по

2).

Решение аналогичной задачи для случая четырёх и более костей «вручную» будет чрезвычайно громоздким. Собственно, смысл данной лабораторной работы как раз и состоит в том, чтобы разобраться, как найти (точнее, оценить) вероятность некоторого сложного события, если подсчитать эту вероятность «вручную» трудно или невозможно.

9

Статистическое определение вероятности

Пусть в каждом испытании некоторое событие может наступить с одинаковой вероятностью p . Относительной частотой события A в серии n испы-

таний называется отношение числа m наступлений этого события к общему числу испытаний:

w(A) = m .	(1.2)
n

Приведённая формула напоминает классическое определение вероятности (1.1), но смысл величин m и n в этих формулах различается. Классическое определение опирается на теоретический подсчёт элементарных исходов, а в формуле (1.2) фигурируют эмпирические (опытные) значения общего числа испытаний и числа наступлений события.

Теорема Бернулли. При неограниченном возрастании числа однородных независимых испытаний с практической достоверностью (т.е. с вероятностью, близкой к 1) можно утверждать, что относительная частота события (1.2) будет сколь угодно близка к вероятности этого события в отдельном испытании:

( ε > 0),( δ > 0),( n > 0) : P( w − p < ε) >1−δ , или w →P(A), n → ∞

p

(«сходимость по вероятности»). Благодаря теореме Бернулли, мы имеем возможность статистически оценивать такие вероятности, которые вряд ли могут быть вычислены теоретически (например, вероятность попадания снаряда в цель или вероятность рождения ребёнка определённого пола). Такое определение вероятности называется статистическим.

Статистическое определение вероятности может применяться и в тех случаях, когда теоретический подсчёт вероятности события возможен, но затруднителен. Для этого надо смоделировать изучаемое случайное событие, точнее говоря, многократно имитировать опыт, в котором это событие может наступать. Метод, реализующий данную схему, называется методом МонтеКарло.

Сведения о методе Монте-Карло

Методом Монте-Карло называется метод решения различных математических задач при помощи моделирования случайных событий и случайных величин и статистической оценки их характеристик. Название «Монте-Карло» произошло от одноимённого города в княжестве Монако, известного своими казино, ибо одним из простейших приборов для моделирования случайных чисел является рулетка.

Теоретически сам метод возник давно и не раз использовался в теории вероятностей и математической статистике. Однако моделирование случайных событий и величин вручную (например, с помощью той же рулетки, игральной

10

кости, монеты) − весьма трудоёмкий процесс. Поэтому серьёзное развитие метод Монте-Карло получил с конца 1940-х годов (в США) с появлением и совершенствованием компьютеров.

Метод Монте-Карло используется для решения задач физики, теории массового обслуживания, экономики, биологии − всё перечислить невозможно.

Задание для лабораторной работы

Вданной работе методом Монте-Карло должны быть решены задачи, рассмотренные выше в примерах 1, 2 и 3, а также более сложная задача, в которой число брошенных костей равно 4.

Задание 1.1. Подбрасываются: (1.1.1) одна игральная кость; (1.1.2) две игральных кости; (1.1.3) три игральных кости; (1.1.4) четыре игральных кости.

Вкачестве случайного события рассматривается появление определённого суммарного числа очков на брошенных костях. (Например, при бросании двух костей могут наступить следующие события: «2», «3», …, «12»). Необходимо в каждой из предложенных задач (1.1.1)- (1.1.4) найти (оценить) вероятности всех возможных событий, проведя 10000 испытаний.

Смысл настоящей работы состоит в том, чтобы, моделируя описанный опыт (подбрасывание игральных костей) с помощью генератора случайных чисел, получить (на основе случайных выборок объёма 10000) статистические оценки вероятностей случайных событий и убедиться, где это возможно, в том, что они (оценки) достаточно близки к истинным значениям вероятностей. Таким образом, вероятностная задача заменяется задачей статистической, в чём и состоит суть метода Монте-Карло.

Инструкция по выполнению задания в Excel

1. Создайте в рабочем листе Excel следующую таблицу:

	A	B	C	D	E	F	G	H	I
1	№	1-я	2-я	3-я	4-я	Одна	Две	Три	Четыре
		кость	кость	кость	кость	кость	кости	кости	кости
2

В первом столбце таблицы должен стоять номер испытания. Введите в ячейку A2 формулу

=1.

В ячейку A3 введите формулу

11

=A2+1.

Адрес (в данном случае A2) удобнее набирать не с клавиатуры, а щёлкая мышкой по нужной ячейке.

В последующие ячейки этого столбца будет вводиться аналогичная формула с помощью автозаполнения. Однако эту операцию удобнее провести не для каждого столбца в отдельности, а для столбцов A-I разом. Пока же продолжим формирование строки 2.

2. В столбцах B-E должны находиться результаты бросания первой, второй, третьей и четвёртой костей соответственно – случайные числа (1, 2, 3, 4, 5, 6 с равной вероятностью). Используем функцию СЛЧИС (). Для этого активизируем ячейку B2, вызовем Вставку функций (кнопка f x на панели инстру-

ментов), в окне Категория выберем Математические, в окне Выберите функцию – СЛЧИС(). Однако с тем же успехом можно просто ввести в ячейку формулу =СЛЧИС() с клавиатуры. Эта функция даёт равномерно распределённую в интервале (0; 1) случайную величину. Формула =6*СЛЧИС()+1 будет давать равномерное распределение в интервале (1; 7).

Функция ОТБР(…) из списка математических отбрасывает часть числа после запятой. Таким образом, формула

=ОТБР(6*СЛЧИС()+1)

будет давать именно то, что нужно (числа 1, 2, 3, 4, 5, 6 с равной вероятностью).

Введём эту формулу в ячейку B2. Нет необходимости вводить её заново в ячейки C2, D2, E2. Выделим ячейку B2. Подведём курсор к правому нижнему углу ячейки так, чтобы он принял вид чёрного крестика, нажмём на левую кнопку мыши и, удерживая её, выделим ячейки C2:E2 (автозаполнение).

3.В ячейках F2:I2 должны находиться формулы, вычисляющие сумму выпавших очков (в четырёх различных задачах с разным числом брошенных костей). В ячейку F2 просто введём =B2, в ячейку G2 формулу =F2+C2, а к ячейкам H2 и I2 применим автозаполнение от «источника» G2.

Обратите внимание, что при автозаполнении формула из ячейки G2 не просто скопировалась, а приняла вид =G2+D2 для ячейки H2 и =H2+E2 для ячейки I2. Относительные ссылки корректируются при автозаполнении и копировании, что и произошло. В данном случае нас это устраивает! Если перед буквой и/или номером стоит знак доллара, например, $A$1, то ссылка на столбец и/или строку является абсолютной. Абсолютные ссылки не корректируются при копировании и автозаполнении. В дальнейшем мы будем пользоваться этим приёмом, когда это будет необходимо.

4.Выделим диапазон B2:I2. Подведём курсор к правому нижнему углу ячейки I2 так, чтобы он принял вид чёрного крестика, нажмём на левую кнопку мыши и, удерживая её, выделим ячейки B3:I3.

Теперь выделим диапазон A3:I3 и c помощью автозаполнения «растянем» таблицу до 10000-го номера испытания.

12

5.Когда таблица велика и не помещается на экране, удобно закрепить строку заголовков. Для этого щёлкните по ячейке B2, войдите в меню Окно и выберите Закрепить области. Теперь, даже если вы переместитесь вниз таблицы, названия столбцов останутся на экране.

6.Теперь перейдём к заданию формул для подсчёта числа наступивших событий. Если рассматривать совокупно все четыре задачи (1.1.1)-(1.1.4) (с разным количеством брошенных костей), то возможными являются события «1», «2», «3», …, «24». Поэтому в диапазоне J10002:J10025 введём соответствующие числа: 1, 2, 3, …, 24 (с помощью автозаполнения, подобно тому, как выше мы вводили номер испытания). Нам необходимо в каждой из четырёх задач подсчитать, сколько раз наступило то или иное событие во всей серии (10000) испытаний. С этой целью введём в ячейку F10002 формулу

=СЧЁТЕСЛИ(F$2:F$10001;$J$10002).

Функция СЧЁТЕСЛИ(диапазон; условие) подсчитывает число непустых ячеек в диапазоне, удовлетворяющих заданному условию. В данном случае будет подсчитываться число единиц, выпавших при 10000 подбрасываний первой кости, поскольку в ячейку J10002 введено число 1. Значки $ нужны для того, чтобы применить автозаполнение ячеек G10002:I10002 от «источника» F10002. Сделав это автозаполнение, мы увидим, что диапазон, являющийся первым аргументом функции, сдвигается вправо, а адрес ячейки, в которой записано условие (второй аргумент) остаётся неизменным.

7. Щелчком мыши активизируйте любую свободную ячейку рабочего листа и раз за разом нажимайте на клавишу Delete. При каждом нажатии будет генерироваться новая выборка объёма 6×10000 , и, следовательно, должны появляться новые значения в ячейках F10002:I10002. Однако на самом деле, в ячейках G10002:I10002 будут оставаться нули, так как при бросании двух, трёх или четырёх костей сумма очков не может оказаться равной 1. Значение в ячейке F10002 будет колебаться вокруг числа 10000 / 6 ≈1667 , т.к. в среднем единица выпадает в каждом шестом испытании.

8.Теперь в формулах, введённых в ячейки F10002:I10002 изменим адрес второго аргумента, убрав один значок доллара: $J10002. После этого выделим ячейки F10002:I10002 и выполним автозаполнение вниз до строки 10025 включительно. Расчёт ячеек может занять некоторое время в зависимости от быстродействия компьютера. В ячейку F10026 введите формулу =СУММ(F10002:F10025) и выполните автозаполнение ячеек G10026:I10026. Во всех ячейках диапазона F10026:I10026 должно появиться значение 10000 (число испытаний).

9.Осталось лишь ввести в таблицу формулы для подсчёта вероятностей событий. Как сказано выше, статистическое определение вероятности состоит в том, что мы приравниваем вероятность события к относительной частоте его наступления в серии однородных независимых опытов. Следовательно, к примеру, вероятность того, что при бросании трёх игральных костей в сумме выпадет 10 очков, приближённо равна количеству таких испытаний, в которых это

13

событие произошло, делённому на полное число испытаний (бросаний трёх костей) и т.д. Эту часть работы предлагаем читателю выполнить самостоятельно. На рисунке показано, как может выглядеть в результате описанных действий электронная таблица.

				Рис. 1.1. Электронная таблица результатов
0,18
0,16
0,14									Одна кость
0,12									Две кости
0,1									Три кости
0,08									Четыре кости
0,06
0,04
0,02
0
1	2	3	4	5	6	7	8	9	10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

Рис. 1.2. Вероятности появления определённой суммы очков при бросании разного числа игральныхкостей (статистическое определение)

14

По полученному распределению вероятностей событий постройте диаграмму (рис. 1.2). Ещё раз поясним, что при каждой реализации значения в таблице будут обновляться, т.к. случайные числа всякий раз генерируются заново. Однако в силу высокой репрезентативности выборки оценки вероятностей будут меняться незначительно, и каждый раз будут близки к истинным значениям вероятностей. Убедитесь, что это действительно так в задачах (1.1.1), (1.1.2) и (1.1.3).

Инструкция по выполнению задания в Mathcad

Для решения поставленных в лабораторной работе задач необходимо будет написать несколько программ-функций.

Рассмотрим сначала алгоритм решения поставленных задач. Моделирование подбрасывания игральных костей предполагает получе-

ние случайным образом числа выпавших очков (целых чисел от 1 до 6). Для этого будем использовать две встроенные в Mathcad функции: rnd(х) и ceil(z). Функция rnd(х) генерирует случайное число, равномерно распределенное на интервале (0, х). Функция ceil(z) возвращает наименьшее целое, большее или равное z. Суперпозиция (комбинация) этих функций вида ceil(rnd(6)) даст нам искомое целое число от 1 до 6. Например, после обращения к функции rnd(6) мы получили число 1,674. Функция ceil(1,674) определит число 2 как наименьшее целое, большее 1,674. Обращаясь m раз к комбинации указанных функций, мы моделируем опыт с бросанием m игральных костей. Способ обращения к встроенным функциям рассмотрим ниже.

В данной лабораторной работе должны быть решены 4 задачи с подбрасыванием от 1 до 4 костей соответственно. Многократно (в нашем случае 10000 раз) моделируя опыт с подбрасыванием соответствующего числа костей, мы должны подсчитать сколько раз выпала та или иная сумма очков. Для решения сформулированных четырех задач нам понадобятся 4 программы-функции; назовем их f1, f2, f3, f4. Первая из них будет формировать вектор для подсчета количества выпадений соответственно 1, 2, 3, 4, 5 или 6 очков при многократном бросании 1 кости. Этот вектор содержит 6 элементов. Вторая, третья и четвертая программы-функции формируют векторы для подсчета количества появления тех или иных сумм при многократном бросании 2, 3 и 4 костей соответственно. Максимальная сумма выпавших очков при бросании двух костей равна 12 (выпало 2 шестерки), при бросании 3 костей – 18, и при бросании 4 костей – 24. Следовательно, полученные векторы будут содержать 12, 18 и 24 элемента соответственно. Разделив каждый элемент полученных векторов на число проведенных опытов (в нашем случае 10000), получим статистические оценки вероятностей появления определенного суммарного числа очков на брошенных костях.

Перейдем к описанию программ-функций.

Программы-функции в Mathcad содержат конструкции, во многом подобные конструкциям таких языков как Pascal или FORTRAN: операторы присваивания, операторы циклов, условные операторы и т.д. Такой способ называется

15

программированием в программе-функции и состоит из двух этапов: (1) описание программы-функции; (2) вызов программы-функции.

Описание программы-функции размещается в рабочем документе перед вызовом программы-функции и включает в себя имя программы-функции, список формальных параметров и тело программы-функции.

Каждая программа-функция Mathcad имеет оригинальное имя, использованием которого осуществляется обращение к этой программе-функции. Через это же имя (и только через это имя) “возвращается” в рабочий документ результат выполнения программы-функции.

После имени программы-функции идет список формальных параметров, заключенный в круглые скобки. В качестве формальных параметров могут использоваться имена простых переменных, массивов и функций. Формальные параметры отделяются друг от друга запятой. Программа-функция может не иметь формальных параметров и тогда данные передаются через имена переменных, определенных выше описания программы-функции.

Тело программы-функции включает любое число локальных операторов присваивания, условных операторов и операторов цикла, а также вызов других программ-функций и функций пользователя.

На рис. 1.3 приведены программы-функции f4(n) и f3(n), которые формируют векторы для подсчета количество появления тех или иных сумм выпавших очков при многократном бросании 4 и 3 костей соответственно. Рассмотрим подробно описание программы-функции f4(n).

Заметим, что по умолчанию в Mathcad нумерация строк (столбцов) матриц начинается с 0. Чтобы нумерация начиналась с 1 нужно сразу либо присвоить системной переменной ORIGIN значение 1 (именно это сделано в нашем примере), либо с помощью команды Инструменты Параметры документа

Встроенные переменные задать начальный индекс массива равным 1.

ORIGIN :=1

f4(n) := for i 1.. 24 bi ← 0

for k 1.. n

a1 ← ceil(rnd (6))

a2 ← ceil(rnd (6))

a3 ← ceil(rnd (6))

a4 ← ceil(rnd (6))

i ← a1 + a2 + a3 + a4 bi ← bi + 1

for i 1.. 24

b← bi i n

b

f3(n) := for i 1.. 18 b i ← 0

for k 1.. n

a1 ← ceil(rnd (6))

a2 ← ceil(rnd (6))

a3 ← ceil(rnd (6)) i ← a1 + a2 + a3 b i ← b i + 1

for i 1.. 18

b ← b i i n

b

16

Рис. 1.3. Программы-функции для отыскания числа появления тех или иных сумм выпавших очков при многократном бросании 4 и 3 костей

Для ввода в рабочий документ описания программы-функции необходимо выполнить следующие действия:

−ввести имя программы-функции (f4) и список формальных параметров, заключенный в круглые скобки (в нашем случае формальным параметром является n – число проведенных опытов);

−ввести символ двоеточие « : », что приведет к появлению знака присваивания : = ;

−открыть наборную панель Программирование, показанную ниже, и щелкнуть кнопкой Add line (Добавить линию).

На экране появится вертикальная черта и вертикальный столбец с двумя полями ввода для ввода операторов, образующих тело программы-функции.

Имя программы-функции		Поле 1

	f (n) :=
					Поле 2
Формальный параметр

Поставив курсор в поле 1, добавим дополнительные строки для ввода операторов путем повторного нажатия кнопки Add line панели программирования нужное количество раз. Самое нижнее поле (поле 2) всегда предназначено для определения возвращаемого программой значения.

Внимание! Если вам необходимо вставить дополнительную строку в уже готовую функцию, то

–поставьте курсор в конец оператора, после которого нужно вставить

строку;

–нажимая несколько раз клавишу «пробел», добейтесь полного выделения данного оператора, а затем нажмите кнопку Add line панели программирования, после выделенного оператора появится новая пустая строка.

Первые две строки программного кода использованы для присвоения значений, равных нулю всем элементам вектора b с помощью оператора цикла for.

Для ввода этого оператора нужно поставить курсор в первую строку поля 1 и щелкнуть на кнопке for наборной панели Программирование. На экране появятся следующие поля ввода:

17

Поле 1

Поле 2

for

Поле 3

В поле ввода 1 введите имя параметра цикла (переменная i). Затем в поле ввода 2 введите диапазон значений параметра цикла, используя для этого дис-

кретный аргумент (символ « ..», указывающий на изменение переменной в за-

данных пределах вводится клавишей « ; »). В поле ввода 3 вводятся операторы, составляющие тело цикла. В нашем случае тело цикла состоит из одного оператора присваивания bi←0. Чтобы набрать нижний индекс нужно нажать на клавиатуре клавишу со знаком [ (открывающая квадратная скобка). Чтобы вый-

ти из режима набора индексов, нужно нажать управляющую клавишу « → » на клавиатуре.

Внимание!

–Не вводите с клавиатуры имена программных операторов, поскольку они будут восприняты Mathcad не корректно. Для их вставки можно применять лишь соответствующие значки наборной панели Программирования или сочетания клавиш, которые приведены в тексте всплывающей подсказки.

–Присваивание в пределах программ-функций, в отличие от документов

Mathcad, производится с помощью оператора Local Definition (Локальное присваивание), который вставляется нажатием кнопки с изображением стрелки ←

на панели Программирование. Ни оператор присваивания « := », ни оператор

вывода « = » в пределах программ не применяются.

Для удаления того или иного оператора или поля ввода из тела програм- мы-функции, нужно заключить его в выделяющую рамку и нажать клавишу

[Delete].

Следующий оператор цикла имеет более сложную структуру, так как тело цикла состоит из нескольких операторов. В программе они объединены дополнительной вертикальной чертой. Чтобы вставить такую черту нужно после введения оператора цикла for k 1 . . n поставить курсор в местозаполнитель следующей строки и щелкнуть по кнопке Add line в панели программирования. Щелкнув по этой кнопке еще несколько раз, создайте дополнительные поля ввода (строки) для записи операторов тела цикла.

Для обращения к встроенным функциям ceil(z) и rnd(x) нужно щелкнуть на

кнопке . Нажав эту кнопку, мы вызовем панель Insert Function (вставить функцию), в которой имеются 2 поля: Function Category (тип функции или категория) и Function Name (имя функции) .

18

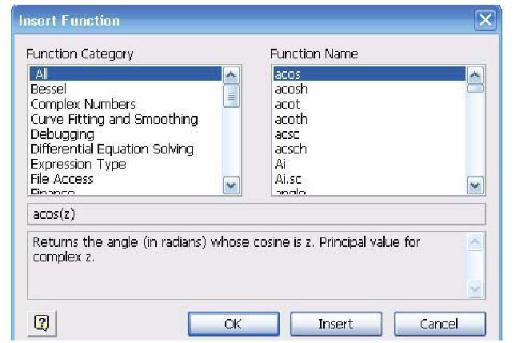
Для функции ceil(z) нужно выбрать категорию Truncation and RoundOff (Отбрасывание и округление), затем имя ceil (не путайте с Ceil) и нажать ОК. Поставив курсор в появившемся в скобках местозаполнителе, нужно аналогично вызвать функцию rnd. Ее можно найти в категории Random Numbers (Случайные числа). В качестве аргумента в появившейся функции поставьте цифру 6.

Аналогичным образом введите все оставшиеся операторы. В конце про- граммы–функции мы использовали еще один оператор цикла, чтобы определить значения статистических вероятностей выпадения той или иной суммы очков. Как сказано выше, статистическое определение вероятности состоит в том, что мы приравниваем вероятность события к относительной частоте его наступления в серии однородных независимых опытов. Следовательно, вероятность того, что при бросании m игральных костей выпадет та или иная сумма очков, приближённо равна количеству таких испытаний, в которых это событие произошло, делённому на полное число испытаний (в нашем случае 10000) .

При вводе формулы обратите внимание, что знак деления вводится клавишей « / ».

Если вы внимательно посмотрите на программу-функцию f3(n), то заметите, что ее легко можно получить из функции f4(n), удалив некоторые строки и внеся небольшие изменения. Заключив программу-функцию f4(n) в выделяющую рамку, скопируйте и вставьте ее в пустое поле рабочего документа, а затем внесите соответствующие исправления. Обратите внимание, что все переменные, используемые внутри программы-функции, являются локальными и вне программы не определены, поэтому мы можем пользоваться для описания разных функций переменными с одинаковыми именами.

19

Аналогичным образом самостоятельно выполните описание программ-

функций f2(n) и f1(n).

Для выполнения программы-функции необходимо обратиться к ее имени с указанием списка фактических параметров. Фактические параметры указывают, при каких конкретных значениях осуществляются вычисления в теле программы. Очевидно, что между фактическими и формальными параметрами должно быть соответствие по количеству, порядку следования и типу. При этом имена фактических параметров при вызове программы-функции могут не совпадать с именами ее формальных параметров.

Обращение к программе-функции должно находиться после описания программы-функции (то есть правее или ниже ее) и к моменту обращения фактические параметры должны быть определены.

Для выполнения программы–функции f1(n) при n=10000 присвоим вектору b1 значение f1(10000). Запишем b1:= f 1(10000) , а затем наберем b1 и на-

жмем клавишу « = ». Аналогично обратимся к остальным программамфункциям, используя векторы b2, b3, b4.

Полученные результаты будут выглядеть примерно следующим образом:

b1:= f 1(10000)				b2 := f 2(10000)			b3 := f 3(10000)			b4 := f 4(10000)
	0.159
						1			1			1
		0.174			1	0		1	0		1	0
					2	0.029		2	0		2	0
b1 =		0.169
					3	0.056		3	4.6·10 -3		3	0
	0.166
					4	0.079		4	0.015		4	1·10-3
		0.163
				b2 =	5	0.114		5	0.027		5	3.3·10-3
	0.169				6	0.138		6	0.047		6	8.7·10-3
					7	0.172		7	0.066		7	0.015
					8	0.141	b3 =			b4 =	8	0.029
								8	0.1
					9	0.108		9	0.113		9	0.045
					10	0.081		10	0.126		10	0.06
					11	0.056		11	0.123		11	0.077
					12	0.028		12	0.122		12	0.093
								13	0.096		13	0.109
								14	0.071		14	0.112
								15	0.048		15	0.103
								16	...		16	...

Для того, чтобы увидеть все значения векторов b3 и b4 нужно щелкнуть мышью на окошке со знаком « … » (многоточие), появится полоса прокрутки, с помощью которой можно сдвигать строки таблицы.

Перейдем к построению графиков.

Для определения значений оси ОХ при построении графиков нам понадобится вектор х с координатами от 1 до 24, который нужно будет предвари-

20

тельно определить в программе.

Сделать это можно различными способами:

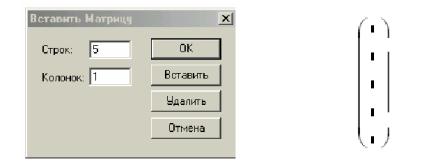
1)с помощью команды Вставка Матрица, или комбинации клавиш Ctrl

+M,

2)щелчком на кнопке панели Матрица

, 3) с использованием дискретного аргумента, когда имеется некоторая явная

зависимость для вычисления элементов через их индексы.

При использовании первых двух способов в появившемся окне ввода матриц и векторов нужно задать необходимое число строк и столбцов и нажать « ОК ». Затем заполнить массив пустых полей в появившемся шаблоне вектора (для не слишком больших массивов)

Третий способ предполагает использовать Дискретные аргументы - особый класс переменных, который в пакете Mathcad часто используются при создании простых циклов. Эти переменные имеют ряд фиксированных значений, либо целочисленных (1 способ), либо в виде чисел с определенным шагом, меняющихся от начального значения до конечного (2 способ).

Name := Nbegin .. Nend,

где Name - имя переменной, Nbegin - ее начальное значение, Nend - ко-

нечное значение, « ..» – символ, указывающий на изменение переменной в заданных пределах (вводится клавишей « ; »). Если Nbegin < Nend, то шаг переменной будет равен +1, иначе –1.

В нашем случае задать вектор с помощью дискретных переменных можно следующим образом:

i :=1. .24

xi :=i

Для создания декартового графика необходимо установить визир в пустом месте рабочего документа. Затем выполнить одно из следующих действий:

–выбрать команду Вставка График Х-У график,

–нажать комбинацию клавиш Shift + @,

–щелкнуть кнопку панели Графики.

21

Появится шаблон декартового графика. Незаполненный шаблон графика представляет собою большой пустой прямоугольник с шаблонами данных в виде темных маленьких прямоугольников, расположенных около осей абсцисс и ординат буду-

щего графика. В средние шаблоны данных надо по-

местить имя переменной у оси абсцисс и задать формулы или поместить имена векторов для функций у оси ординат. Если строятся графики нескольких функций в одном шаблоне, то для их разделения следует использовать запятые. Крайние шаблоны данных служат для указания предельных значений абсцисс и ординат, т. е. они задают масштабы графика. Если оставить эти шаблоны незаполненными, то масштабы по осям графика будут устанавливаться автоматически. Недостаток тут в том, что масштабы, скорее всего, окажутся не вполне удобными (например, будут представлены неокругленными десятичными цифрами) для представления целиком всего графика в максимальном размере.

Для построения графиков полученных векторов b1, b2, b3, b4 поместим их имена через запятую в средний шаблон оси Y. В крайние шаблоны по этой оси поместим значения соответственно 0 и 0.25. В средний шаблон оси Х поместим х, а в крайние шаблоны значения 1 и 24.

Чтобы начать построение графика достаточно щелкнуть за пределами области графика.

Параметры изображения (цвет и толщина линий, координатная сетка, разметка осей, надписи на графиках и др.) проще всего изменить, щелкнув дважды по полю графика и установив настройки в соответствующих окнах.

На рис. 1.4 приведены вкладки окна формирования графика.

В левом нижнем углу первой вкладки имеются точки Boxed (коробочка), Crossed (оси), None (нет). Нажав на первую точку, введем в график оси координат.

Слева и справа вверху имеются строки X-Axes (ось Х) и Primary Y-Axes (первая ось Y), а под ними ряд надписей, левая часть которых относится к оси Х, а правая – к оси Y: Log Scale (логарифмическая шкала) вводит логарифмический масштаб для соответствующей оси; Grid lines (сетка) – ее нажатие вводит сетку на графике; Numbered (оцифровка сетки); Auto Scale (автоматическая оцифровка); Show markers (показ маркеров); Auto grid (автоматическое разбиение сетки). Наличие надписей Enable secondary Y-Axes (возможность второй оси Y) и Secondary Y-Axes (вторая ось Y) дает возможность формировать графики различного масштаба для различных функций.

22

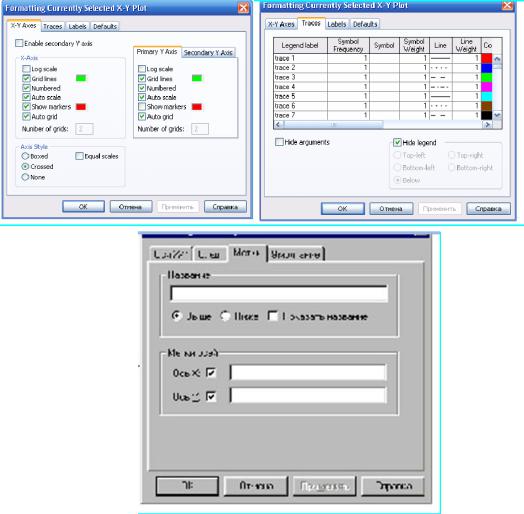
Рис. 1.4. Окно формирования графика

Рассмотрим вторую вкладку. Из ее левого столбца (trace 1, trace 2 и т.д.) следует, что на одном графике можно построить до 16 различных функций. Вводя соответствующие значения в остальные столбцы, можно изменять вид (сплошная линия, пунктир, точки), цвет, толщину и т.д. каждой функции.

На третьей вкладке окна задается заголовок (Title), место его расположения Above (сверху), Beloved (снизу), наименование осей (Axis Labels).

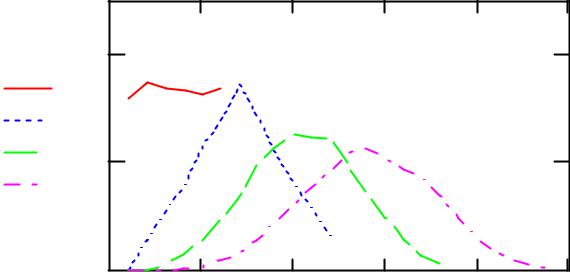
Выбрав те или иные требования к графику, нажмем ОК и получим желаемый результат, подобный приведенному на рис. 1.5.

23

			Статистические оценки вероятностей
b1	0.2
b2
b3
b4	0.1
	0	0	5	10	15	20	25
Рис. 1.5. Вероятности появления определенной суммы очков при бросании разного числа
			игральных костей (статистическое определение)

Заметим, что при одновременном нажатии клавиш Ctrl и F9 значения векторов будут изменяться, т.к. случайные числа всякий раз генерируются заново. Однако в силу высокой репрезентативности выборки, оценки вероятностей будут меняться достаточно слабо, оставаясь близкими к истинным значениям вероятностей.

Дополнительное задание

Задание 1.2. Каждый участник игры бросает: (1.2.1) четыре игральных кости; (1.2.2) пять игральных костей.

Участник, у которого сумма выпавших очков составит ровно 21, получает крупный выигрыш. Оцените вероятность такого выигрыша статистически, по результатам 10000 испытаний. Попробуйте найти точное значение этой вероятности по классическому определению.

Контрольные вопросы

1.Сформулируйте классическое определение вероятности.

2.Дайте определение и приведите расчётные формулы для числа перестановок (без повторяющихся элементов и с повторяющимися элементами), числа сочетаний, числа размещений.

3.Полностью завершите расчёт вероятностей в табл.2 (пример 3).

4.Как вы понимаете смысл теоремы Бернулли и статистического определения вероятности? Приведите примеры применения.

5.Проанализируйте результаты решения задания 1.2.

24

Работа 2

СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ СОБЫТИЙ И ДИСКРЕТНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН

Метод Монте-Карло: три вида единичного жребия и их реализация. Статистическая проверка законов алгебры событий.

Моделирование дискретной случайной величины с произвольным законом распределения

Время на выполнение и защиту – 2 час

Цель работы:

1)уяснение законов алгебры событий;

2)знакомство с видами единичного жребия, применяемыми в методе Монте-Карло для разыгрывания случайных событий и случайных величин;

3)изучение некоторых функций Excel и Mathcad.

Алгебра событий

Суммой событий A и B называется событие S = A + B, которое состоит в наступлении хотя бы одного из них.

Произведением событий A и B называется событие D = AB , состоящее в их совместном появлении.

Определения суммы и произведения событий распространяются на любое (конечное) число слагаемых или сомножителей.

Пример 4. Если A — появление 1 очка, B — 3-х очков, C — 5-ти очков при одном бросании игральной кости, то S = A + B + C — появление нечётного числа очков. Если A — появление дамы, а B — появление пиковой масти при вытягивании одной карты из колоды, то D = AB есть появление пиковой дамы.

События A и B называются несовместными, если они не могут наступить в одном и том же опыте. Ясно, что для таких событий P(AB) = 0 .

Группа событий называется полной, если в результате опыта обязательно наступает хотя бы одно из этих событий.

Два события называются противоположными, если это несовместные события, образующие полную группу.

Пример 5. Рассмотрим в качестве опыта, приводящего к наступлению различных событий, одно бросание игральной кости. Пусть A — появление единицы, B – двойки, C – единицы, тройки или пятёрки, D – четвёрки или шестёрки. Тогда:

— событие A совместно с событием C, но несовместно с событиями B и D;

25

—события A, B, C и D в совокупности образуют полную группу, но даже если событие A исключить, группа не утратит полноты;

—ни одна пара событий, выбранная из группы A, B, C, D, не является парой противоположных событий;

—события C и B + D являются противоположными;

Вероятность суммы событий
Справедлива формула
P(A + B) = P(A) + P(B) − P(AB) .	(2.1)

Из этого основного утверждения вытекает целый ряд очевидных следст-

вий:

1.Если события A и B несовместны, то P(A + B) = P(A) + P(B) .

2.Если события A1, A2, ..., An образуют полную группу несовместных со-

n n

бытий, то P(∑Ai ) =∑P(Ai ) =1.

i=1 i=1

3. Для двух противоположных событий P(A) + P(A) =1.

Формулу для вероятности суммы трёх и более совместных событий мы не рассматриваем. В этом случае гораздо проще «действовать» через противоположное событие.

Пример 6. Найти вероятность того, что при бросании двух монет хотя бы на одной из них выпадет «орёл».

1-ый способ. Согласно классическому определению вероятности, получаем P(A) = 3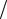4 , т.к. существует 4 равновозможных исхода («орёл»-«орёл»,

«орёл»-«решка», «решка»-«орёл» и «решка-решка»), из которых 3 исхода являются благоприятными.

2-ой способ. Рассматривая событие A как сумму двух событий («орёл» на первой монете, «орёл» на второй монете) по формуле (2.1) для вероятности

суммы получаем P(A) = 12 + 12 − 14 = 34 , где вероятность произведения событий

(т.е. вероятность события «орёл»-«орёл») найдена по классическому определению.

Зависимость событий. Вероятность произведения событий

Условной вероятностью P(A B) называется вероятность события A, вы-

численная при условии, что событие B произошло. Событие A называется зависимым от события B, если P(A B) ≠ P(A) . Зависимость событий всегда взаим-

на, т.е. если A зависит от события B, то и B зависит от события A. Вероятность произведения двух событий определяется формулой

P(AB) = P(A)P(B		A).	(2.2)

26

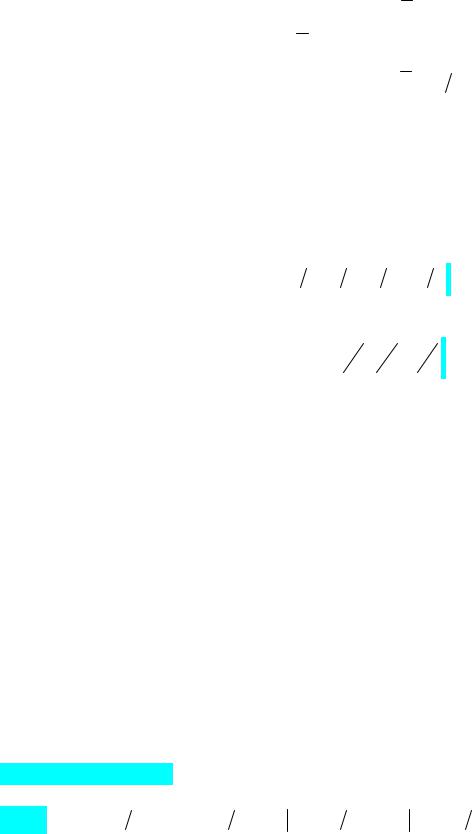
Для независимых событий

P(AB) = P(A)P(B) .

(2.3)

Решим пример 6 ещё одним (уже третьим) способом. Если A – появление хотя бы одного «орла», то противоположное событие A – появление «решек»

на обеих брошенных монетах. Найдём P(A) = 12 12 = 14 как вероятность произ-

ведения независимых событий (2.3). Тогда P(A) =1− P(A) = 3 4.

Пример 7. Студент сдаёт два экзамена: физику и математику. Он оценивает свои шансы получить «отлично» по физике как 1 против 3-х, «отлично» по математике как 1 против 2-х. Каковы шансы студента получить хотя бы одну оценку «отлично» на двух экзаменах?

Введём вероятности отличной сдачи экзаменов: pф =1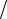4, pм =1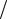3 . Как и

впримере 6, здесь возможны разные способы решения.

1.По формуле (2.1) с учётом (2.3) получим

P(A) = pф + pм − pф pм =1 4 +1 3 −1 12 =1 2.

2. Через понятие противоположного события получим

P(A) =1 − (1 − pф)(1 − pм) =1 − 34 23 = 12 .

Есть и третий способ решения, который состоит в том, чтобы отдельно найти вероятность ровно одной оценки «отлично» и двух оценок «отлично», и затем найденные вероятности сложить. В данном случае этот способ нерационален, однако мы обратимся к нему ниже, в пункте Дискретные случайные величины (пример 9).

Формула полной вероятности

Пусть событие A может произойти вместе с любым из несовместных друг с другом событий H1, H2, ..., Hn, образующих полную группу (они называются гипотезами). Тогда вероятность события A определяется как

n
P(A) = ∑P(Hi )P(A	Hi ) .	(2.4)
i =1

Пример 8. Среди театральных зрителей женщин вдвое больше, чем мужчин. Из каждых 25 мужчин 1 является дальтоником, а среди женщин это заболевание встречается в 10 раз реже. Найти вероятность того, что выбранный наугад театральный зритель — дальтоник.

Обозначим события: Н1 – зритель – мужчина; Н2 – зритель – женщина; А

– зритель – дальтоник.

Тогда P(H1) =1 3; P(H2 ) = 2 3; P(A H1) =1 25; P(A H2 ) =1 250 .

27

Следовательно, по формуле полной вероятности

P( A) = 13 251 + 23 2150 = 75012 = 0,016 .

Дискретные случайные величины

Величина, принимающая в результате опыта заранее неизвестное числовое значение, называется случайной величиной. Случайная величина, имеющая набор изолированных возможных значений, называется дискретной (ДСВ). Законом распределения ДСВ называется правило, по которому каждому возможному значению ставится в соответствие вероятность, с которой случайная величина может принять это значение. Закон распределения может быть задан таб-

лично (ряд распределения), графически (многоугольник распределения) и анали-

тически (формула).

Пример 9. Вернёмся к условиям примера 7, но переформулируем задачу. Студент сдаёт два экзамена: по физике и математике. Вероятность получения «пятёрки» по физике P(A1) =1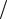4, по математике P(A2 ) =1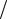3. Найти закон рас-

пределения случайной величины X – числа полученных студентом «пятёрок» на двух экзаменах.

P(X = 0) = P(A1 A2 ) = P(A1) P(A2 ) = 34 23 = 12 ;

P(X =1) = P(A1)P(A2 ) + P(A1)P(A2 ) = 14 23 + 34 13 = 512;

P(X = 2) = P(A1 A2 ) = P(A1)P(A2 ) = 14 13 = 112 .

События, заключающиеся в том, что ДСВ примет свои возможные значения, образуют полную группу несовместных событий. Поэтому сумма вероятностей всех возможных значений ДСВ равна 1 (или стремится к 1, если множество возможных значений бесконечно).

Биномиальный закон распределения

Одним из наиболее известных законов распределения ДСВ является так называемый биномиальный закон.

Случайная величина X, представляющая собой число наступлений некоторого события в серии n испытаний, в каждом из которых вероятность наступления этого события одинакова и равна p, имеет распределение, называемое биномиальным. Это распределение описывается формулой Бернулли

P(X = k) = Cnk pk (1 − p)n−k , k = 0, 1, ..., n ,

(2.5)

где Cnk – число сочетаний из n по k .

28

Пример 10. Пусть случайная величина X – число наступлений некоторого события в серии из 3 испытаний, в каждом из которых вероятность наступления этого события одинакова и равна 1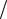4. Тогда X подчинена биномиальному зако-

ну распределения

	P(X = x ) = C						x 1			xi 3			3−xi
																, где x = 0, 3,
								i
			i			3		4			4						i
	или (в табличном виде)
		xi	0					1			2		3
		pi		27				27			9			1
			64					64			64		64

Единичные жребии в методе Монте-Карло

Вработе 1 мы рассматривали применение метода Монте-Карло в задачах

сравновозможными исходами. Теперь рассмотрим общий подход к моделированию случайных событий и величин с помощью так называемых единичных жребиев (т.е. опытов со случайным исходом). Единичный жребий может быть

реализован с помощью генерации случайного числа – значения случайной величины, равномерно распределённой на интервале от 0 до 1 (работа 1). Обозначим такое случайное число через γ . Нас будут интересовать три вида единичного жребия, которые мы рассмотрим последовательно.

Произошло ли данное событие? Пусть нам известно, что событие A имеет вероятность p . Можно условиться считать, что если γ приняло значение

меньше p , то событие A произошло; при γ ≥ p событие не произошло. Вопрос о том, почему «граничный» случай γ = p , трактуется как ненаступление собы-

тия, не имеет никакого практического значения. Учитывая точность компьютерного представления действительных чисел, вероятностью такого совпадения можно просто пренебречь. Во всяком случае, на результат статистического моделирования это никакого влияния не оказывает.

Какое из нескольких событий, образующих полную группу несовме-

стных событий, произошло? Пусть события A1 , A2 , ..., Ak наступают с вероятностями p1 , p2 , ..., pk , образуя полную группу несовместных событий, так что

k

∑ pi =1.

i=1

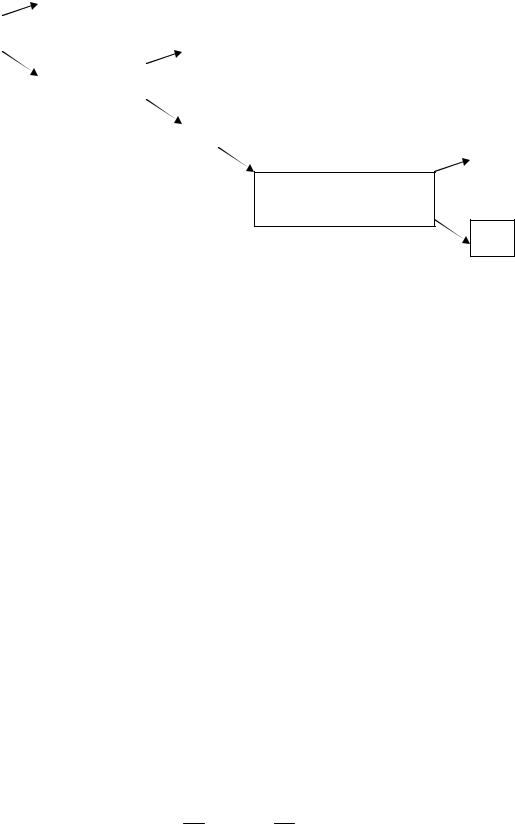
На рис. 2.1 показан алгоритм, который можно принять для определения наступления того или иного события в зависимости от значения случайного числа γ :

29

да			A1
γ < p1				да
						A2
нет
			γ < p1 + p2
				нет
						…
								да	Ak −1

γ < p1 + p2 +...+ pk −1

нет Ak

Рис. 2.1. Алгоритм определения наступления того или иного события в зависимости от значения случайного числа γ

Пусть, например, A1 , A2 , ..., A5 – равновозможные события, образующие пол-

ную группу несовместных событий (т.е. каждое из них имеет вероятность 0,2). Случайное число приняло значение γ = 0,68 . Поскольку

0,2 + 0,2 + 0,2 < 0,68 < 0,2 + 0,2 + 0,2 + 0,2 ,

считаем, что произошло событие A4 .

Какое значение приняла дискретная случайная величина? Рассмот-

рим дискретную случайную величину с известным законом распределения: значения x1 , x2 , ..., xk принимаются с вероятностями p1 , p2 , ..., pk соответст-

венно. Легко понять, что этот случай сводится к предыдущей задаче, поскольку равенства {X = x1}, {X = x2 }, …, {X = xk } можно рассматривать как события

A1 , A2 , ..., Ak . Пусть, например, случайная величина подчинена закону распределения, полученному в примере 10:

xi	0			1			2			3
pi		27			27			9			1
	64			64			64			64

Допустим, что случайное число приняло значение 0,47. Поскольку

2764 < 0,47 < 5464 ,

считаем, что случайная величина X приняла значение 1.

30

Задания для лабораторной работы

Задание 2.1. Смоделировать с помощью метода Монте-Карло случайные события, описанные в примере 8.

Задание 2.2. Смоделировать с помощью метода Монте-Карло ситуацию, описанную в примерах 7 и 9.

Задание 2.3. Разыграть по методу Монте-Карло дискретную случайную величину, описанную в примере 10.

Смысл настоящей работы состоит в том, чтобы, моделируя методом Мон- те-Карло случайные события, в которых отсутствует симметрия исходов, научиться статистически оценивать вероятности событий.

Инструкция по выполнению заданий в Excel

Для выполнения задания 2.1 создадим таблицу следующего вида:

	A	B		C	D	E
1		Доля мужчин в театре			0,333333333
		Вероятность дальтонизма у мужчины			0,04
2
		Вероятность дальтонизма у женщины			0,004
3
	№	Сл. число		Мужчина или женщина?	Сл.число	Дальтоник или нет?
4
5

Вячейку D1 вводим число 1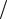3, поскольку по условию на одного мужчину

втеатре приходится две женщины. В ячейки D2 и D3 вводим вероятности дальтонизма у мужчин и женщин соответственно. В ячейки B5 и D5 вводим функцию СЛЧИС(). Для заполнения ячеек C5 и D5 необходимо воспользоваться логической функцией

ЕСЛИ (лог_выражение; значение_если_истина; значение_если_ложь).

Учитывая сформулированные выше правила разыгрывания случайных событий, в ячейку C5 введём =ЕСЛИ(B5<$D$1;"муж";"жен"), а в ячейку D5 более сложное выражение

=ЕСЛИ(C5="муж";ЕСЛИ(D5<$D$2;"да";"нет");ЕСЛИ(D5<$D$3;"да";"нет"))

Значки доллара в адресах некоторых ячеек поставлены для того, чтобы при последующем автозаполнении эти адреса не корректировались.

«Растягиваем» таблицу вниз до испытания №10000 и вычисляем с помощью функции СЧЁТЕСЛИ следующие величины: число мужчин, число женщин, число дальтоников и вероятность дальтонизма у наугад отобранного зрителя. Как мы видели при решении примера 8, эта вероятность равна 0,016. Статистическая оценка вероятности при числе испытаний, равном 10000, как правило, оказывается в пределах 0,014 – 0,018.

Переходим к заданию 2.2. Начнём с моделирования ситуации, описанной в примере 7. Создадим таблицу следующего вида:

31

	A	B		C	D
1	Вероятность «5» по физике		0,25
	Вероятность «5» по математике		0,33333333
2
3	№	По физике «5»?		По математике «5»?	Хотя бы одна
					пятёрка?
4	1	=ЕСЛИ(СЛЧИС()<$C$1;		=ЕСЛИ(СЛЧИС()<$C$2;	=ЕСЛИ(B4="да";"да";
		"да";"нет")		"да";"нет")	ЕСЛИ(C4="да";"да";
					"нет"))
5	…	…		…	…

Обратите внимание на то, что в данном случае, в отличие от задания 2.1, мы не стали вводить специальных столбцов для случайных чисел, а использовали функцию СЛЧИС() как «вложение» в функцию ЕСЛИ (подумайте, почему это было невозможно в задании 2.1). «Растягиваем» таблицу и вычисляем вероятность того, что на двух экзаменах получена хотя бы одна пятёрка, как отношение числа таких испытаний, в которых это произошло, к полному числу испытаний. Статистическая оценка этой вероятности при числе испытаний, равном 10000, как правило, оказывается в пределах 0,49 – 0,51 (точное значение, как мы видели при решении примера 7, равно 0,5).

В примере 9 задача поставлена чуть более широко: найти закон распределения случайной величины X – числа полученных студентом «пятёрок» на двух экзаменах. Решение этой задачи методом Монте-Карло может быть получено с помощью следующей таблицы в EXCEL:

		A		B	C	D
1		Вероятность «5» по физике			0,25
		Вероятность «5» по математике			0,33333333
2
3		№		По физике «5»?	По математике «5»?	«Пятёрок» на двух
						экзаменах
		1		=ЕСЛИ(СЛЧИС()<$C$1;1;0)	=ЕСЛИ(СЛЧИС()<$C$2;1;0)	=B4+C4
4
		…		…	…	…
5

В данном случае нам удобно отображать результат экзамена в виде двоичного кода: если оценка «5», то результат равен 1, в противном случае результат равен 0. В каждом испытании число полученных «пятёрок» суммируется. После этого необходимо подсчитать число испытаний, в которых было получено 0, 1 и 2 «пятёрки» и оценить соответствующие вероятности. Эти оценки должны быть близки к точным значениям вероятностей, полученным при решении примера 9.

Переходим к заданию 2.3. Как было отмечено выше, разыгрывание дискретной случайной величины, по сути дела, сводится к разыгрыванию полной группы событий.

	A	B	C	D	E
1		0	1	2	3
2	№	0,421875	0,421875	0,140625	0,015625
			=ЕСЛИ(B3<$B$2;0;
3	1	=СЛЧИС()	32
			ЕСЛИ(B3<$B$2+$C$2;1;
			ЕСЛИ(B3<$B$2+$C$2+$D$2;2;3)))
4	…	…	…	…	…

Вдиапазон ячеек B1:E2 вводим заданный ряд распределения, в ячейку C3

–формулу, которая определяет значение случайной величины в зависимости от значения случайного числа. После «растягивания» таблицы для проверки подсчитайте число испытаний, в которых случайная величина приняла значения 0, 1, 2 и 3 и оцените соответствующие вероятности.

Инструкция по выполнению задания в Mathcad

При решении поставленных задач нам нужно будет проверять выполнение некоторых условий, для чего мы используем так называемый условный оператор. Для его ввода необходимо щелкнуть на кнопке if панели программирования или нажать клавишу « } ». На экране появляется конструкция с двумя полями.

Поле 1

if		Поле 2

В поле 2 вводится логическое выражение (в простейшем случае это выражение отношений). В поле 1 вводится выражение (как правило, арифметическое), которое используется, если проверяемое логическое выражение принимает значение 1.

Логическое выражение. Логическим выражением называется конструкция, составленная из выражений отношений, знаков логических операций и круглых скобок. Значение логического выражения вычисляется слева направо с учетом известного правила о приоритете операций. Список приоритетов (по их убыванию):

•круглые скобки;

•логическая операция И (знак на панели «булева алгебра»);

•логическая операция ИЛИ (знак на панели «булева алгебра»).

Условный оператор может находиться только внутри тела программы- функции. Например:

Поле 1		Поле 2

y( x)					if
								Поле 3

В поле 3 задается выражение, значение которого используется, если логическое выражение равно 0. Для ввода в поле 3 необходимо:

•заключить это поле в выделяющую рамку;

•щелкнуть на кнопке otherwise панели программирования;

33

•в оставшемся поле ввести соответствующее выражение.

Выражение, стоящее перед словом otherwise выполняется только в том

случае, если не выполнено заданное перед этим условием.

В программе можно использовать несколько следующих друг за другом условных операторов с одним выражением перед словом otherwise.

Если в поле 3 ввести оператор без слова otherwise, то этот оператор будет выполняться всегда вне зависимости от выполнения выше заданных условных операторов.

Ниже приведена программа-функция для решения задания 2.1.

f8(n) := for i 1..3 ci ← 0

for i 1..n

a← rnd (1)

b← rnd (1)

c1 ← c1 + 1

if a <

1

3

c2

← c2

+ 1

otherwise

c

3

← c

3

+ 1

if

b

<

0.04 a <

1

b

< 0.004 a ≥

1

3

3

c3 ←

c3

n

c

Поскольку в программе используются векторы, то перед началом работы присвоим системной переменной ORIGIN значение 1.

Здесь, как и в работе 1, переменные a и b – это случайные числа из интервала (0, 1). Первый и второй элементы вектора с будем использовать для подсчета количества мужчин и женщин в театре соответственно, третий элемент используем для подсчета дальтоников. Если число a < 1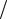3, то считаем, что

случайный зритель − мужчина, иначе – женщина. Далее, если a < 13 и при

этом b < 0,04 (вероятность дальтонизма у мужчин), то перед нами мужчинадальтоник. Если же a ≥ 1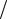3 и при этом b < 0,004 (вероятность дальтонизма у

женщин), то перед нами женщина-дальтоник. Объединение этих условий дает нам число дальтоников из рассмотренных 10000 человек (третья строка снизу в программе-функции).

Перед выходом из программы-функции определим вероятность дальтонизма у наугад отобранного зрителя, разделив полученное число дальтоников на число проведенных испытаний. Как мы видели при решении примера 8, эта вероятность равна 0,016. Статистическая оценка вероятности при числе испы-

34

таний, равном 10000, как правило, оказывается в пределах 0,014 – 0,018. В этом легко убедиться, нажав несколько раз сочетание клавиш <Ctrl> + <F9>. Значения вектора при этом будут изменяться, т.к. случайные числа всякий раз генерируются заново.

Переходим к заданию 2.2. Начнём с моделирования ситуации, описанной в примере 7.

Если полученное случайное число a < 0,25, то считаем, что по физике получена пятерка, если b < 1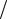3 – то по математике получена пятерка. В про-

грамме мы подсчитываем число испытаний, когда было выполнено хотя бы одно (первое или второе) из этих условий (знак на панели «булева алгебра»). Вероятность того, что на двух экзаменах получена хотя бы одна пятёрка, вычисляем как отношение числа испытаний, в которых это произошло, к полному числу испытаний.

Таким образом, программа-функция f7(n) для решения примера 7 имеет совсем простой вид.

f7(n) := c ← 0

for i 1.. n

a← rnd(1)

b← rnd(1)

c ← c + 1 if a < 0.25 b < 13 c ← cn

c

Статистическая оценка этой вероятности при числе испытаний, равном 10000, как правило, оказывается в пределах 0,49 – 0,51 (точное значение, как мы видели при решении примера 7, равно 0,5).

В примере 9 задача поставлена чуть более широко: найти закон распределения случайной величины X – числа полученных студентом «пятёрок» на двух экзаменах. Для подсчета количества пятерок, полученных на двух экзаменах,

зададим вектор с, имеющий три элемента. Первый элемент отведем для подсчета испытаний, в которых не получено ни одной «пятёрки» (одновременное выполнение условий a > 0,25 и b > 13), второй – одна «пятёрка», и третий –

две «пятёрки» (одновременное выполнение условий a ≤ 0,25 и b ≤ 13). После

этого необходимо оценить соответствующие вероятности, поделив полученные результаты на количество испытаний. Эти оценки должны быть близки к точным значениям вероятностей, полученным при решении примера 9.

Программа-функция f9(n) приведена ниже.

35

f9(n) := for i 1..3 ci ← 0

for i 1..n

a← rnd (1)

b← rnd (1)

c1	← c1 + 1	if	a > 0.25 b >	1
				3
c3	← c3 + 1	if	a ≤ 0.25 b ≤		1
					3
c2	← c2 + 1	otherw ise

for i 1..3

c← ci i n

c

Переходим к заданию 2.3.

Как было отмечено выше, разыгрывание дискретной случайной величины, по сути дела, сводится к разыгрыванию полной группы событий. Будем считать, что случайная величина подчинена биномиальному закону распределения (пример 10): число наступлений некоторого события в серии из 3 испытаний с заданной вероятностью наступления события pz. Случайная величина может принимать значения 0, 1, 2, 3. Соответствующие им вероятности вычислим с помощью встроенной функции dbinom(k,n,pz). Находим эту функцию в категории Probability Density (Плотность вероятности).

Для подсчета числа испытаний, в которых случайная величина приняла то или иное из указанных значений, используем вектор с, имеющий 4 элемента. Первый элемент используется для подсчета количества испытаний, в которых случайная величина приняла значение равное нулю (когда сгенерированное случайное число имеет значение меньшее, чем p0 ). Второй элемент – для

подсчета числа испытаний со значением случайной величины, равным единице (когда случайное число получило значение большее, чем p0 , но меньшее, чем

p0 + p1 ). Аналогично определяем 3 и 4 элементы. Для оценки соответствую-

щих вероятностей поделим полученные результаты на количество испытаний. Программа-функция для решения поставленной задачи приведена ниже.

36

f10(n ,pz) :=	for		i 0 .. 3
			ci ← 0
			pi ← dbinom(i ,3 ,pz)
	p0 ← p 0
	p1 ← p0 + p1
	p2 ← p1 + p2
	for		i 1 .. n
			a ← rnd (1)
			c0 ← c0 + 1 if a ≤ p0
			c1 ← c1 + 1 if p0 < a ≤ p1
			c2 ← c2 + 1 if p1 < a ≤ p2
			c3 ← c3 + 1 otherwise
	for		i 0 .. 3
	c		←	ci
		i		n
	c

Обратите внимание, что в данном случае нумерация элементов вектора начинается с 0, а не с 1, как в предыдущих заданиях данной работы. Поэтому, если ранее в данном файле вы присваивали системной переменной ORIGIN значение 1, то теперь перед программой-функцией следует записать

ORIGIN:=0.

Для выполнения программы-функции необходимо обратиться к ее имени с указанием фактических параметров (n = 10000, pz = 1/4).,

Дополнительное задание

Задание 2.4. Студент сдаёт тест, который включает в себя 32 задания по 8 разделам (дидактическим единицам), по 4 задания в каждом разделе. Дидактическая единица считается освоенной, если не менее чем 2 задания из 4 решены правильно. Студент считается сдавшим тест, если он освоил все 8 дидактических единиц. Известно, что студент правильно решает каждое тестовое задание с вероятностью p . С какой вероятностью он сдаст тест?

Задачу решить следующими способами.

2.4.1. Аналитически найти вероятность освоения дидактической единицы как вероятность суммы несовместных событий (2, 3 или 4 правильных ответа), вычисляя отдельные слагаемые с помощью формулы Бернулли

37