Федеральное государственное автономное

образовательное учреждение

высшего профессионального образования

«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»

Институт управления бизнес-процессами и экономики

Кафедра бизнес-информатики

Отчет о лабораторной работе №2

По дисциплине «Методы моделирования и прогнозирования экономики»

Вариант 6

Студент УБ 11-01 __________ Ивкина В.А.

Руководитель __________ Чубаров А.В.

Красноярск 2013

Оглавление

Теоретические сведения 3

Постановка задачи 7

Алгоритмическая часть 9

Заключение 16

Теоретические сведения

К математическим задачам линейного программирования относят исследования конкретных производственно-хозяйственных ситуаций, которые в том или ином виде интерпретируются, как задачи об оптимальном использовании ограниченных ресурсов.

Круг задач, решаемых при помощи методов линейного программирования достаточно широк:

1. задача об оптимальном использовании ресурсов при производственном планировании;

2. задача о планировании состава продукции;

3. задача о нахождении оптимальной комбинации различных видов продукции для хранения на складах;

4. анализ размещения предприятия, перемещение грузов.

В общем виде задача линейного программирования с m ограничениями и n переменными имеет следующий вид:

Целевая функция имеет вид:

(1)

При ограничениях,

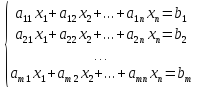(2)

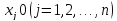
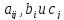- заданные постоянные величины.

Минимизировать линейную функцию 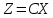при ограничениях:

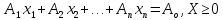(3)

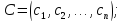
Где, 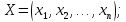CX - скалярное произведение;

Векторы

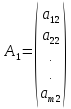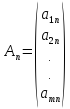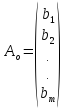, , … ,,(4)

состоят соответственно из коэффициентов при неизвестных и свободных членов.

Минимизировать линейную функцию 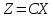при ограничениях:

(5)

- матрица-строка;

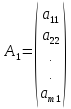
A = (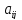) - матрица системы;

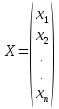- матрица-столбец;

- матрица столбец.

Минимизировать линейную функцию -

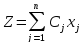(6)

При ограничениях:

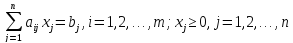(7)

Задача линейного программирования заключается в нахождении оптимального значения функции при соблюдении существующих ограничений.

Вектор 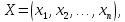удовлетворяющий вышеуказанным ограничениям, называется планом задачи линейного программирования.

Оптимальным планом задачи линейного программирования называется план, доставляющий наибольшее (наименьшее) значение линейной функции.

Задачи линейного программирования могут решаться несколькими методами:

1. Геометрический метод.

2. Симплекс-метод.

3. Двойственный симплекс-метод.

Если система ограничений задачи линейного программирования представлена в виде системы линейных неравенств с двумя переменными, то такая задача может быть решена геометрически. Таким образом, данный метод решения задач линейного программирования имеет очень узкие рамки применения.

Однако метод представляет большой интерес с точки зрения выработки наглядных представлений о сущности задач линейного программирования.

Геометрический (или графический) метод предполагает последовательное выполнение ряда шагов. Ниже представлен порядок решения задачи линейного программирования на основе ее геометрической интерпретации.

1. Сформулировать ЗЛП.

2. Построить на плоскости {х1, х2} прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств.

3. Найти полуплоскости, определяемые каждым из ограничений задачи.

4. Найти область допустимых решений.

5. Построить прямую c1x1 + c2x2 = h, где h - любое положительное число, желательно такое, чтобы проведенная прямая проходила через многоугольник решений.

6. Перемещать найденную прямую параллельно самой себе в направлении увеличения (при поиске максимума) или уменьшения (при поиске минимума) целевой функции.

7. Определить координаты точки максимума (минимума) функции и вычислить значение функции в этой точке.

В основу симплексного метода положена идея последовательного улучшения получаемого решения.

Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины многогранника ограничений к соседней, в которой целевая функция принимает лучшее (или, по крайней мере, не худшее) значение до тех пор, пока не будет найдено оптимальное решение - вершина, где достигается оптимальное значение функции цели (если задача имеет конечный оптимум).

Таким образом, имея систему ограничений, приведенную к канонической форме (все функциональные ограничения имеют вид равенств), находят любое базисное решение этой системы, заботясь только о том, чтобы найти его как можно проще. Если первое же найденное базисное решение оказалось допустимым, то проверяют его на оптимальность. Если оно не оптимально, то осуществляется переход к другому, обязательно допустимому базисному решению. Симплексный метод гарантирует, что при этом новом решении целевая функция, если и не достигнет оптимума, то приблизится к нему (или, по крайней мере, не удалится от него). С новым допустимым базисным решением поступают так же, пока не отыщется решение, которое является оптимальным.

Процесс применения симплексного метода предполагает реализацию трех его основных элементов:

1. способ определения какого-либо первоначального допустимого базисного решения задачи.

2. правило перехода не к худшему решению.

3. критерий проверки оптимальности найденного решения.

Симплексный метод включает в себя ряд этапов и может быть сформулирован в виде четкого алгоритма. Задачи с небольшим числом переменных и ограничений могут быть решены симплексным методом вручную.

Теория математического линейного программирования позволяет не только получать оптимальные планы с помощью эффективных вычислительных процедур, но и делать ряд экономически содержательных выводов, основанных на свойствах задачи, которая является двойственной по отношению к исходной ЗЛП.

Правила получения двойственной задачи:

1. Если в исходной задаче ищется максимум целевой функции, то в двойственной ей - минимум.

2. Коэффициенты при переменных в целевой функции одной задачи являются свободными членами системы ограничений другой задачи.

3. В исходной ЗЛП все функциональные ограничения - неравенства вида «≤», а в задаче, двойственной ей, - неравенства вида «≥».

4. Коэффициенты при переменных в системах ограничений взаимно двойственных задач описываются матрицами, транспонированными относительно друг друга.

5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой.

6. Условие неотрицательности переменных сохраняется в обеих задачах.