
Чубаров лаба 1
.docxФедеральное государственное автономное
образовательное учреждение
высшего профессионального образования
«СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
Институт управления бизнес-процессами и экономики
Кафедра бизнес-информатики
ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №1
По дисциплине «Методы моделирования и прогнозирования экономики»
Вариант 6
Студент УБ 11-01 __________ Ивкина В.А.
Руководитель __________ Чубаров А.В.
Красноярск 2013
Оглавление
Постановка задачи 6
Алгоритмическая часть 7
Заключение 9
Теоретические сведения
Метод наименьших квадратов (МНК) - математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений.
Он может использоваться для решения таких систем уравнений, когда количество уравнений превышает количество неизвестных, для поиска решения в случае нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции.
МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным.
Впервые метод наименьших квадратов был использован Лежандром в 1806 году для решения задач небесной механики на основе экспериментальных данных астрономических наблюдений.
Пусть дана система
уравнений
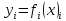 ,
,
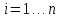 ,
,
где -
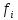 некоторые
функции,
некоторые
функции,
 -
некоторые известные значения,
-
некоторые известные значения,
x - набор неизвестных (искомых) переменных.
Наиболее точную
зависимость переменных Y
от X
можно установить путем приближения
функции
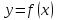 ,
к другой функции
,
к другой функции
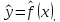 то
есть провести сглаживание экспериментальной
зависимости.
то
есть провести сглаживание экспериментальной
зависимости.
Суть МНК заключается в том, чтобы найти такие значения, при которых минимизируется сумма квадратов отклонений (1):
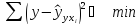 (1)
(1)
В частности, МНК может использоваться для решения системы линейных уравнений. Построение линейной регрессии сводится к оценке ее параметров - a и b . Из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной. Чтобы найти минимум функции надо вычислить частные производные по каждому из параметров a и b и приравнять их к нулю. Для оценки параметров a и b существует система (2):
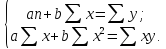 (2)
(2)
Решая систему уравнений, найдем искомые оценки параметров a
и b. Можно воспользоваться следующими готовыми формулами, которые
следуют непосредственно из решения системы (3):
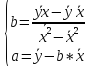 (3)
(3)
где
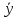 - среднее значение результативного
признака;
- среднее значение результативного
признака;
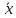 – среднее значение
фактора;
– среднее значение
фактора;
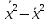 - дисперсия признака
x;
- дисперсия признака
x;
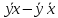 – ковариация
признаков x
и y.
– ковариация
признаков x
и y.
Существует показатель, который определяет тесноту связи между Y - результирующий признак и X - фактор, а именно коэффициент корреляции, который рассчитывается по формуле (4):
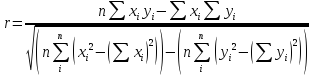 (4)
(4)
где - коэффициент корреляции;
- коэффициент корреляции;
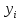 - результативный
признак;
- результативный
признак;
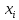 - фактор, влияющий
на результативный признак.
- фактор, влияющий
на результативный признак.
Линейный коэффициент
корреляции находится в пределах
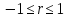 .
Чем ближе абсолютное значение r
к единице, тем сильнее зависимость
между факторами.
.
Чем ближе абсолютное значение r
к единице, тем сильнее зависимость
между факторами.
Чем меньше отличается абсолютная величина r от единицы, тем ближе к линии регрессии располагаются экспериментальные точки. Если коэффициент корреляции равен нулю, то переменные x и y называют некоррелированными.
Для того чтобы оценить значимость коэффициента корреляции, применяется t - критерий Стьюдента. Вычисленное значение критерия Стьюдента определяется по формуле (5):
 (5)
(5)
где n - объем выборки;
Значение t
сравнивается с табличным значением
tтабл.,
при заданном уровне значимости
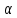 и степенях свободы
и степенях свободы
 Если tфакт
больше
tтабл.,
то коэффициент корреляции значительно
отличается от нуля.
Если tфакт
больше
tтабл.,
то коэффициент корреляции значительно
отличается от нуля.
Чтобы определить параметры квадратичной функции, необходимо составить уравнение (6):
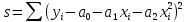 (6)
(6)
Для этой функции запишем систему линейных уравнений (7):
 (7)
(7)
Для нахождения
параметров
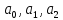 необходимо
решить вышеуказанную систему алгебраических
уравнений.
необходимо
решить вышеуказанную систему алгебраических
уравнений.
Постановка задачи
-
Используя метод наименьших квадратов аппроксимировать функцию Q=f(s), заданную таблично в многочлен второй степени вида : Q=a1+a2s+a3s2.
-
Построить линию тренда и сравнить результаты.
В качестве исходных данных имеем значения s и Q, заданные таблично (табл.1)
Таблица 1 - Исходные данные
|
N |
s |
Q |
|
1 |
1 |
5,21 |
|
2 |
1,25 |
4,196 |
|
3 |
1,5 |
3,759 |
|
4 |
1,75 |
3,672 |
|
5 |
2 |
4,592 |
|
6 |
2,25 |
4,621 |
|
7 |
2,5 |
5,758 |
|
8 |
2,75 |
7,173 |
|
9 |
3 |
9,269 |
Алгоритмическая часть
Выполним расчеты, которые необходимы для решения системы уравнений (табл.2).
Таблица 2 - Расчеты, необходимые для решения системы уравнений.
|
s |
Q |
s^2 |
s^4 |
s^4 |
sQ |
s(Q^2) |
|
1 |
5,21 |
1 |
1 |
1 |
5,21 |
27,1441 |
|
1,25 |
4,196 |
1,5625 |
1,953125 |
2,441406 |
5,245 |
22,00802 |
|
1,5 |
3,759 |
2,25 |
3,375 |
5,0625 |
5,6385 |
21,19512 |
|
1,75 |
3,672 |
3,0625 |
5,359375 |
9,378906 |
6,426 |
23,59627 |
|
2 |
4,592 |
4 |
8 |
16 |
9,184 |
42,17293 |
|
2,25 |
4,621 |
5,0625 |
11,39063 |
25,62891 |
10,39725 |
48,04569 |
|
2,5 |
5,758 |
6,25 |
15,625 |
39,0625 |
14,395 |
82,88641 |
|
2,75 |
7,173 |
7,5625 |
20,79688 |
57,19141 |
19,72575 |
141,4928 |
|
3 |
9,269 |
9 |
27 |
81 |
27,807 |
257,7431 |
|
18 |
48,25 |
39,75 |
94,5 |
236,7656 |
104,0285 |
666,2844 |
Составим матрицу коэффициентов, используя систему уравнений :
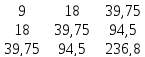
Составим обратную матрицу с помощью функции «МОБР» в excel:
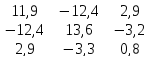
Умножим обратную матрицу на правую часть системы уравнений с помощью функции «МУМНОЖ» в excel и получим коэффициенты уравнения:
А=351,65
В=-1404,58
С=1261,41
Получим функцию : Q= 351,65s2-1404,58s+1261,41
Далее строим график данной функции и на нем линию тренда (рис.1):
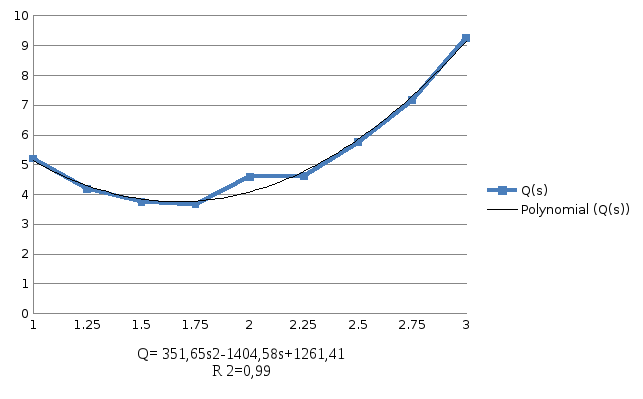
Рисунок 1. Линия график функции с линией тренда.
Линия тренда не отклоняется от заданных значений и точно отражает тенденцию.
Заключение
Использовав МНК аппроксимировали функцию Q=f(s), заданную таблично многочленом второй степени, получили модель вида Q= 351,65s2-1404,58s+1261,41. Построили линию тренда и сравнили результаты.
При
оценке результатов можно отметить, что
линия тренда не отклоняется от заданных
значений и точно отражает тенденцию,
так как
полученное при построении линии тренда
значение коэффициента детерминации
для экспоненциальной зависимости равен
0,99 ( ).
).
