РОССИЙСКИЙ ХИМИКО-ТЕХНЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
ИМ. Д.И. МЕНДЕЛЕЕВА
КУРСОВАЯ РАБОТА ПО ДИСКРЕТНОЙ МАТЕМАТИКЕ
«АЛГОРИТМ ПОИСКА ГАМИЛЬТОНОВЫХ ГРАФОВ.
ЗАДАЧА КОММИВОЯЖЕРА»
Выполнена студентами группы КС-30:
Игониной Мариной
Кучинским Никитой
Пироговой Татьяной
Преподаватель: Шайкин Александр Николаевич
Вариант № 2.
Москва, 2007.
Содержание:
I. Введение…………………………………………………………………………………………. 3
II. Условия существования гамильтоновых графов …………………………………………….. 4
III. Задача коммивояжера (ЗК)………………………………………………………………….….. 5
IV. Алгоритмы решения ……………………………………………………………………………. 6
IV.1. Поиск с возвращением………………………………………………………………….. 7
IV.2. “Жадный” алгоритм решения ЗК………………………………………………………. 8
IV.3. “Деревянный” алгоритм решения ЗК………………………………………………….. 9
IV.4. Метод лексикографического перебора………………………………………………… 10
IV.5. Применение алгоритма Дейкстры к решению ЗК…………………………………..... 11
IV.6. Метод выпуклого многоугольника для решения ЗК…………………………………. 12
IV.7. Генетические алгоритмы……………………………………………………………….. 14
V. Практическое применение задачи коммивояжера в химии и химической технологии…… 18
I. Введение
Основные определения из теории графов.
Пусть V - непустое конечное множество. Через V(2) обозначим множество всех двухэлементных подмножеств из V. Графом G называется пара множеств (V, E), где E — произвольное подмножество из V(2). Элементы множеств V и E называют соответственно вершинами и ребрами графа G. Граф G(V, E) называется полным, если любая пара его вершин соединена хотя бы в одном направлении.
Маршрутом (или путем) в графе G называется чередующаяся последовательность вершин и ребер v0, e1, v1, …, vt−1, et, vt+1, в которой ei = vi−1vi (1 ≤ i ≤ t). Такой маршрут кратко называют (v0, vt)-маршрутом и говорят, что он соединяет v0 c vt; в свою очередь вершины v0, vt — это концевые вершины указанного маршрута. Длиной маршрута называют количество содержащихся в нем ребер. Заметим, что в обыкновенном графе маршрут полностью определяется последовательностью v0, v1, …, vt своих вершин. Если v0=vt, то (v0, vt)-маршрут называется замкнутым.
Цепь — это маршрут без повторяющихся ребер. Цепь называется простой цепью, если в ней нет повторяющихся вершин, кроме, быть может, совпадающих концевых вершин. Замкнутая простая цепь называется циклом (или контуром).
Гамильтоновой цепью графа называется его простая цепь, которая проходит через каждую вершину графа точно один раз. Цикл графа, проходящий через каждую его вершину, называется гамильтоновым циклом. Граф называется гамильтоновым, если он обладает гамильтоновым циклом.
Указанные названия цепей и циклов связаны с именем Уильяма Гамильтона (Hamilton W.), который в 1859 году предложил следующую игру-головоломку: требуется, переходя по очереди от одной вершины додекаэдра к другой вершине по его ребру, обойти все 20 вершин по одному разу и вернуться в начальную вершину.
додекаэдр
Стоит учесть, что гамильтонов цикл не обязательно содержит все ребра графа. Любой граф G можно превратить в гамильтонов граф, добавив достаточное количество вершин. Для этого, например, достаточно к вершинам v1,...,vt графа G добавить вершины u1,...,ut и множество ребер {(vi,ui)} {(ui,vi+1)}.
II. Условия существования гамильтонова цикла.
Для графов нет критерия, однозначно определяющего гамильтоновы они, или нет. Большинство известных фактов имеет вид: «если граф G имеет достаточное количество ребер, то граф является гамильтоновым».
Следующая теорема, доказанная Поша (Posa L.), дает достаточное условие того, что неориентированный граф является гамильтоновым. Она обобщает результаты, полученные ранее Оре (Ore O.) и Дираком (Dirac G.A.).
Теорема Поше
Пусть G имеет p ≥ 3 вершин. Если для всякого n, 1 ≤ n ≤ (p−1) ⁄ 2, число вершин со степенями, не превосходящими n, меньше чем n, и для нечетного p число вершин степени (p−1) ⁄ 2 не превосходит (p−1) ⁄ 2, то G — гамильтонов граф.
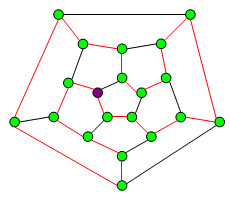
Приведенное достаточное условие не является необходимым. Кубический граф, изображенный на рисунке, гамильтонов, хотя ясно, что он не удовлетворяет условиям теоремы. Однако условия теоремы неулучшаемы, поскольку при их ослаблении новое условие уже не будет достаточным для гамильтоновости графа.
