TIPS_1_laba / Игра Перестановка

Игра «Перестановка»

1. Прямой метод.

Для начала нужно взять ряд чисел (букв или других предметов), которые при перестановке образуют новый ряд.

Например:  

Шаг 1.

Для осуществления перестановки берем наш ряд  и делим его на пары. Чтобы определить количество пар берем общее количество предметов и вычитаем из него единицу (l=n-1), в нашем случае 4-1=3, то есть делим ряд на три пары:

1 пара - 

2 пара - 

3 пара - 

Шаг 2.

Берем 1ую пару и делим ее 2 части: первая часть -  и вторая часть -  , проделываем то же самое и с остальными парами.

Шаг 3.

Берем то, что осталось от 1 ряда () и в его начало ставим 1 часть пары, и в конец ряда ставим 2 часть пары и получаем новый ряд  , то же самое проделываем с остальными парами и получаем в результате три новых ряда.

Шаг 4.

Любой ряд можно перестанавливать не до бесконечности, имеется определенное количество рядов (комбинаций) , которые могут быть образованы в результате перестановок, оно рассчитывается по формуле: n=n!/2-12/2=6

2. Обратный метод.

Для начала нужно взять ряд чисел (букв или других предметов), которые при перестановке образуют новый ряд.

Например:  

Шаг 1.

Для осуществления перестановки берем наш ряд  и делим его на пары. Чтобы определить количество пар берем общее количество предметов и вычитаем из него единицу (l=n-1), в нашем случае 4-1=3, то есть делим ряд на три пары:

1 пара - 

2 пара - 

3 пара - 

Шаг 2.

Берем 1ую пару и делим ее 2 части: первая часть -  и вторая часть -  , проделываем то же самое и с остальными парами.

Шаг 3.

Берем то, что осталось от 1 ряда () и в его начало ставим 2 часть пары, и в конец ряда ставим 1 часть пары и получаем новый ряд  , то же самое проделываем с остальными парами и получаем в результате три новых ряда.

Шаг 4.

Любой ряд можно перестанавливать не до бесконечности, имеется определенное количество рядов (комбинаций), которые могут быть образованы в результате перестановок, оно рассчитывается по формуле: n=n!=4!=12

Полная схема преобразования состояний прямым преобразованием представлена на рисунке 3.

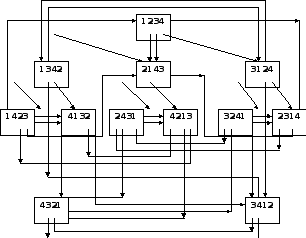
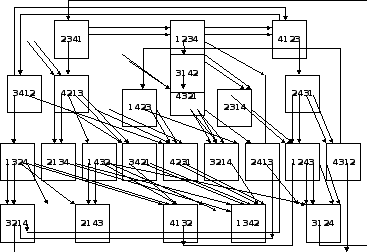
Матрица инцидентности для прямого преобразования.

	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10	x11	x12
y1	1	0
y2	1		0
y3	1			0
y4		1			0
y5		1				0
y6		1		0
y7			1				0
y8			1					0
y9	0		1
y10				1					0
y11				1						0
y12		0		1
y13	0				1
y14			0		1
y15					1	0
y16						1					0
y17					0	1
y18						1						0
y19							1	0
y20							1		0
y21							1			0
y22							0	1
y23						0		1
y24					0			1
y25									1			0
y26									1	0
y27									1		0
y28									0	1
y29			0							1
y30	0									1
y31								0			1
y32											1	0
y33							0				1
y34				0								1
y35		0										1
y36											0	1

Матрица смежности

	1234	1342	2143	3124	1423	4132	2431	4213	3241	2314	3412	4321
1234	0	1	1	1	1	0	0	0	0	1	0	0
1342	1	0	0	1	1	1	0	0	0	0	1	0
2143	1	0	0	0	1	0	1	1	0	1	0	0
3124	1	1	0	0	0	0	0	0	1	1	1	0
1423	1	1	1	0	0	1	0	1	0	0	0	0
4132	0	1	0	0	1	0	0	1	0	0	1	1
2431	0	0	1	0	0	0	0	1	1	1	0	1
4213	0	0	1	0	1	1	1	0	0	0	0	1
3241	0	0	0	1	0	0	1	0	0	1	1	1
2314	1	0	1	1	0	0	1	0	1	0	0	0
3412	0	1	0	1	0	1	0	0	1	0	0	1
4321	0	0	0	0	0	1	1	1	1	0	1	0

Представление пространства поиска.

а) Каким образом организовано пространство состояний?

б) Существуют ли в пространстве состояний не пересекаемые подмножества состояний, каким образом их можно определить?

в) Какие существуют отношения между состояниями пространства поиска?

а) Организацию пространства состояний удобно представить в виде ориентированного графа (в дальнейшем  орграфа), где множество вершин орграфа сопоставимо с состояниями, а множество дуг графа сопоставимы с операторами преобразующими состояния множества.

Представление пространства состояний в виде орграфа позволяет выделить дополнительные свойства и организацию состояний. Свойства определяются отношением подмножеств, входящих и выходящих дуг.

Рассмотрим наиболее весомые условия соотношений множеств Yⁱⁿ{y_j} (входящих дуг) и Y^out{y_j} (выходящих дуг), устанавливающие организацию орграфа G: Если для всякой вершины x_iX орграфа G, выполняются условия: Yⁱⁿ{y_j}=n-1 и Y^out{y_j}=n-1, то орграф представляет собой замкнутую структуру.

Свойства некоторых вершин так же влияют на организацию орграфа:

1. Если для некоторой вершины x_iX орграфа G, выполняются условия: Yⁱⁿ{y_j}1 и Y^out{y_j}=, то такая вершина x_i является «терминальной». Терминальная вершина указывает на то, что для соответствующего состояния s_i, множество применимых к нему операторов: F=. Такое состояние не может быть далее преобразовано.

2. Если для некоторой вершины x_iX орграфа G, выполняются условия: Yⁱⁿ{y_j}= и Y^out{y_j}1, то такая вершина x_i является «корневой». Корневая вершина не может быть порождена ни одной вершиной орграфа G. Так, если корень дерева не представляет собой кольцо, то в дереве есть только одна корневая вершина.

Итак, граф G задает пространство состояний, т.е. пространство, в котором осуществляется поиск решения. Построение пространства осуществляется с помощью следующего процесса. Берется некая вершина, к ней применяются все возможные операторы, порождающие все дочерние вершины. Этот процесс называют процессом раскрытия вершин. Если получена целевая вершина, то она не раскрывается. Процесс построения пространства состояний заканчивается, когда все нераскрытые вершины являются целевыми, или терминальными (т.е. вершинами, к которым нельзя применить никаких операторов). В связи с тем, что пространство состояний может содержать бесконечное количество вершин, на практике процесс порождения пространства ограничивают либо временем, либо объемом памяти.