ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

ИНСТИТУТ КОСМИЧЕСКИХ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

Лабораторная работа №1 «Анализ процедур генерации»

Выполнила: ст.гр КИ08-16

Демидова О.Е..

Горбунова В.А.

Мухамедьярова А.В.

Проверил: Перфильев Д.А.

Красноярск 2010

Тема: Анализ работы «слепых» методов поиска при решении задач в пространстве состояний.

Цель: Дать представление о возможности использования «слепых» методов поиска в решении задач.

Задача: Провести относительный анализ эффективности использования различных процедур генерации «слепыми» методами поиска при различных условиях их проведения.

1. Описание задачи. 

Игра «Перестановка»

1. Прямой метод.

Для начала нужно взять ряд чисел (букв или других предметов), которые при перестановке образуют новый ряд.

Например: 

Шаг 1.

Для осуществления перестановки берем наш ряд  и делим его на пары. Чтобы определить количество пар берем общее количество предметов и вычитаем из него единицу (l=n-1), в нашем случае 4-1=3, то есть делим ряд на три пары:

1 пара - 

2 пара - 

3 пара - 

Шаг 2.

Берем 1ую пару и делим ее 2 части: первая часть -  и вторая часть -  , проделываем то же самое и с остальными парами.

Шаг 3.

Берем то, что осталось от 1 ряда () и в его начало ставим 1 часть пары, и в конец ряда ставим 2 часть пары и получаем новый ряд  , то же самое проделываем с остальными парами и получаем в результате три новых ряда.

Шаг 4.

Любой ряд можно перестанавливать не до бесконечности, имеется определенное количество рядов (комбинаций) , которые могут быть образованы в результате перестановок, оно рассчитывается по формуле: n=n!/2-12/2=6

2. Обратный метод.

Для начала нужно взять ряд чисел (букв или других предметов), которые при перестановке образуют новый ряд.

Например: 

Шаг 1.

Для осуществления перестановки берем наш ряд  и делим его на пары. Чтобы определить количество пар берем общее количество предметов и вычитаем из него единицу (l=n-1), в нашем случае 4-1=3, то есть делим ряд на три пары:

1 пара - 

2 пара - 

3 пара - 

Шаг 2.

Берем 1ую пару и делим ее 2 части: первая часть -  и вторая часть -  , проделываем то же самое и с остальными парами.

Шаг 3.

Берем то, что осталось от 1 ряда () и в его начало ставим 2 часть пары, и в конец ряда ставим 1 часть пары и получаем новый ряд  , то же самое проделываем с остальными парами и получаем в результате три новых ряда.

Шаг 4.

Любой ряд можно перестанавливать не до бесконечности, имеется определенное количество рядов (комбинаций), которые могут быть образованы в результате перестановок, оно рассчитывается по формуле: n=n!=4!=12

Целью задачи является получение из некоторой заданной последовательности знаков, требуемую последовательность этих же знаков.

В качестве знаков могут быть использованы любые символы. Но предлагается использовать набор не повторяющихся цифр. Количество состояний (возможных сочетаний цифр) S =n!, где n – количество цифр в состоянии.

Задачей является поиск заданного состояния в образованном графе.

Рассмотрим пример преобразований на наборе цифр от 1 до 4.

Преобразование состояний «прямым» преобразованием. выполняется следующим образом:

1) В состоянии выделяются пары чисел (i, i+1). Например, для состояния 1234, парами являются (1,2), (2,3) и (3,4), (их количество n –1 = 3);

2) Первое число пары i переносится в начало состояния, а второе i+1 в конец состояния (см. рисунок 1).

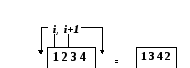
Рис.1.

При «обратном» преобразовании первое число пары i переносится в конец состояния, а второе i+1 в начало состояния (см. рисунок 2).

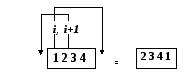
Рис.2.

Таким образом, всегда может быть сформировано (n – 1) состояний. На следующем этапе в полученных состояниях также выделяются пары, и алгоритм преобразования состояний повторяется до условия окончания поиска.

Рассмотрим пример преобразований так же на наборе цифр от 1 до 4.

Полная схема преобразования состояний прямым преобразованием представлена на рисунке 3.

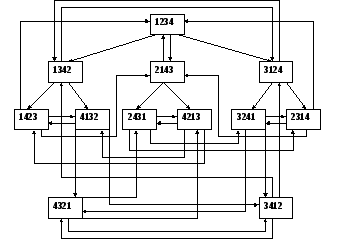
Рис.3.

Полная схема преобразования состояний обратным преобразованием представлена на рисунке 4.

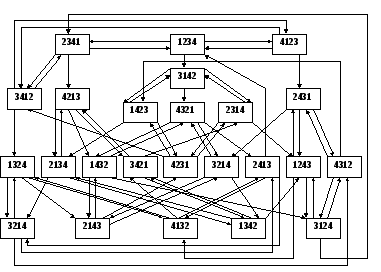
Рис. 4.

Дополнительно организацию состояний можно отобразить с помощь матриц смежности и инцидентности. Матрица смежности позволяет представить бинарные отношения между вершинами орграфа. Отношение смежности обозначается «1», если между вершинами x_i и x_i+1 существует дуга y_j, иначе «0». Матрица инцидентности позволяет представить отношения между количеством входящих и выходящих дуг некоторой вершины x_iG. Отношение обозначается «1», если дуга y_j выходит из вершины x_i, иначе «0» (если дуга y_j входит в вершину x_i).

	1234	1342	2143	3124	1423	4132	2431	4213	3241	2314	3412	4321
1234	0	1	1	1	1	0	0	0	0	1	0	0
1342	1	0	0	1	1	1	0	0	0	0	1	0
2143	1	0	0	0	1	0	1	1	0	1	0	0
3124	1	1	0	0	0	0	0	0	1	1	1	0
1423	1	1	1	0	0	1	0	1	0	0	0	0
4132	0	1	0	0	1	0	0	1	0	0	1	1
2431	0	0	1	0	0	0	0	1	1	1	0	1
4213	0	0	1	0	1	1	1	0	0	0	0	1
3241	0	0	0	1	0	0	1	0	0	1	1	1
2314	1	0	1	1	0	0	1	0	1	0	0	0
3412	0	1	0	1	0	1	0	0	1	0	0	1
4321	0	0	0	0	0	1	1	1	1	0	1	0

Матрица смежности для прямого преобразования

В таблице смежности как столбцы, так и строки соответствуют вершинам графа. В каждой ячейке этой матрицы записывается число, определяющее наличие связи от вершины-строки к вершине-столбцу (либо наоборот). Если связь вежду вершинами имеется то ставим «1», иначе «0». Заметим, что в главной диагонали получившейся матрицы стоят «0». Также, содержание i-того столбца соответствует содержанию i-той строки, так как и там, и там записаны вершины графа(например 1-ый столбец: 0 1 1 1 1 0 0 0 0 1 0 0 и первая строка:0 1 1 1 1 0 0 0 0 1 0 0). Еще можно увидеть, что каждая строка(столбец) имеет пять «1», хотя из матрицы смежности следует, что каждая вершина имеет 6 дуг, это объясняется тем, что при прямом преобразовании каждая вершина имеет одну двойную связь(т.е. каждая вершина имеет парную себе вершину между которыми возникает связь «вход-выход» и «выход-вход»)

Матрица инцидентности для прямого преобразования.

	x1	x2	x3	x4	x5	x6	x7	x8	x9	x10	x11	x12
y1	1	0
y2	1		0
y3	1			0
y4		1			0
y5		1				0
y6		1		0
y7			1				0
y8			1					0
y9	0		1
y10				1					0
y11				1						0
y12		0		1
y13	0				1
y14			0		1
y15					1	0
y16						1					0
y17					0	1
y18						1						0
y19							1	0
y20							1		0
y21							1			0
y22							0	1
y23						0		1
y24					0			1
y25									1			0
y26									1	0
y27									1		0
y28									0	1
y29			0							1
y30	0									1
y31								0			1
y32											1	0
y33							0				1
y34				0								1
y35		0										1
y36											0	1

Матрица инцидентности — одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (дуга и вершина). Столбцы матрицы соответствуют вершинам, строки — ребрам. Если y_j выходит из вершины x_i то «1», иначе «0». Заметим, что в строке каждого y_j имеется одна «1» и один «0», это значит что каждая дуга из одной вершины выходит и в другую входит, следовательно в графе нет корневых вершин(которые имеют только выходы). А также, каждая вершина имеет ранвое количество входов и выходов.

Например, для поиска по лучу всегда раскрывается только одна любая пара из состояния. Для поиска в глубину всегда раскрываются все пары одного любого состояния. Для «параллельного» поиска всегда раскрывается одна определенная пара из всех состояний фронта. Для поиска в ширину все пары всех состояний.

Условием поиска состояния будет нахождение соответствующего числа (набора символов) в графе. Если искомая комбинация заданных символов не найдена, то поиск заканчивается при окончании преобразований графа.

Условием окончания преобразования состояний будет являться множество дуг, исходящих из вершины хi, (родительской вершины), и множество вершин (называемых дочерними вершинами), в которые эти дуги приводят. Множество дуг, исходящих из вершины xi, должно соответствовать множеству операторов, которые могут быть применены к состоянию, соответствующему вершине хi. При использовании в состояниях 4х символов, количество входящих в состояние опереторов должно быть равно количеству выходящих из него операторов и равно n-1, т.е 3. После чего построение графа заканчивается.

2. Представление пространства поиска.

а) Каким образом организовано пространство состояний?

б) Существуют ли в пространстве состояний не пересекаемые подмножества состояний, каким образом их можно определить?

в) Какие существуют отношения между состояниями пространства поиска?

а) Организацию пространства состояний удобно представить в виде ориентированного графа (в дальнейшем  орграфа), где множество вершин орграфа сопоставимо с состояниями, а множество дуг графа сопоставимы с операторами преобразующими состояния множества.

Представление пространства состояний в виде орграфа позволяет выделить дополнительные свойства и организацию состояний. Свойства определяются отношением подмножеств, входящих и выходящих дуг.

Рассмотрим наиболее весомые условия соотношений множеств Yⁱⁿ{y_j} (входящих дуг) и Y^out{y_j} (выходящих дуг), устанавливающие организацию орграфа G: Если для всякой вершины x_iX орграфа G, выполняются условия: Yⁱⁿ{y_j}=n-1 и Y^out{y_j}=n-1, то орграф представляет собой замкнутую структуру.

Свойства некоторых вершин так же влияют на организацию орграфа:

1. Если для некоторой вершины x_iX орграфа G, выполняются условия: Yⁱⁿ{y_j}1 и Y^out{y_j}=, то такая вершина x_i является «терминальной». Терминальная вершина указывает на то, что для соответствующего состояния s_i, множество применимых к нему операторов: F=. Такое состояние не может быть далее преобразовано.

2. Если для некоторой вершины x_iX орграфа G, выполняются условия: Yⁱⁿ{y_j}= и Y^out{y_j}1, то такая вершина x_i является «корневой». Корневая вершина не может быть порождена ни одной вершиной орграфа G. Так, если корень дерева не представляет собой кольцо, то в дереве есть только одна корневая вершина.

Итак, граф G задает пространство состояний, т.е. пространство, в котором осуществляется поиск решения. Построение пространства осуществляется с помощью следующего процесса. Берется некая вершина, к ней применяются все возможные операторы, порождающие все дочерние вершины. Этот процесс называют процессом раскрытия вершин. Если получена целевая вершина, то она не раскрывается. Процесс построения пространства состояний заканчивается, когда все нераскрытые вершины являются целевыми, или терминальными (т.е. вершинами, к которым нельзя применить никаких операторов). В связи с тем, что пространство состояний может содержать бесконечное количество вершин, на практике процесс порождения пространства ограничивают либо временем, либо объемом памяти.

б) В пространстве состояний существуют не пересекаемые подмножества.

Родовые признаки (одинаковое количество символов, цифры в последовательности не повторяются) выделяют пространство состояний, следовательно, родовые признаки не пересекаемых подмножеств не равны пустому множеству, т.е. К^R≠Ø

На практике требуется обеспечить полноту поиска, т.е. организовать поиск так, чтобы все целевые вершины были найдены, если они существуют. Надежным способом обеспечения полноты является полный перебор всех вершин. Для задания процесса перебора необходимо определить. порядок, в котором будут перебираться вершины графа. Обычно выделяют два основных способа поиска: поиск в глубину (сначала раскрывается та вершина, которая была построена самой последней) и поиск в ширину (вершины раскрываются в том же порядке, в котором они порождаются).

Но при реализации игры «перестановка» следует учитывать условия:

1) Если количество знаков в состоянии 2m и применяется прямое правило, то мощность пространства поиска будет равным n!/2.

2) Если количество знаков в состоянии 2m-1 и применяется прямое правило, то мощность пространства поиска будет равным n!.

3) Если количество знаков в состоянии 2m и применяется обратное правило, то мощность пространства поиска будет равным n!.

4) Если количество знаков в состоянии 2m-1 и применяется обратное правило, то мощность пространства поиска будет равным n!/2.

Эти условия необходимы для того, чтобы определить существуют ли в пространстве состояний не пересекаемые подмножества состояний. Пример: если следовать условиям 2 и 3, то таких состояний не появится т.к из родительской вершины, состоящей из n символов можно образовать n! возможных комбинаций, а если следовать условям 1 и 4, то можно образовать только половину возможных состояний и в пространстве состояний окажутся непересекаемые вершны. Можно сделать вывод, что обязательним условием существованя искомой вершины является проверка количества символов в состоянии на четность/нечетность.

в) Отношения между состояниями пространства.

Пространство поиска в составе пространства состояний образуется за счет обобщения видовых признаков некоторых состояний. В этом случае обобщенные видовые признаки дополняют множество родовых признаков данных состояний, образуя собственное пространство поиска в пространстве состояний или класс состояний.

Каждое состояние пространства состояний получено прямым или обратным преобразованием.

Глубина пространства поиска меньше либо равна n-1, где n-число цифр в состоянии.

Элементы пространства поиска различны.