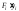- •Раздел 5. Геометрические характеристики плоских сечений
- •Контрольные вопросы к 5 разделу.
- •Раздел 6. Кручение стержней круглого сечения
- •6.1. Общие сведения
- •6.2. Расчеты на прочность и жесткость стержней при кручении
- •И углов поворота поперечных сечений
- •1. По условию прочности:
- •2. По условию жесткости:
- •Контрольные вопросы к 6 разделу
- •Раздел 7. Плоский поперечный изгиб прямых брусьев
- •7.1. Общие сведения
- •7.2. Подбор сечения балки
- •7.3. Определение прогибов балки и углов поворотов сечений.
Раздел 5. Геометрические характеристики плоских сечений
При решении ряда задач, связанных с прочностными и деформационными расчётами деталей и элементов конструкций, возникает необходимость определения основных геометрических характеристик их поперечных сечений (ГХС). К ним относятся площади поперечных сечений, статические моменты и моменты инерции.
Эти характеристики достаточно часто используются при расчёте стержней как простых форм сечений (круг, прямоугольник, треугольник и т.п.), так и сложных видов сечений (профильное сечение, составное сечение и др.). Определение ГХС требуется в задачах изгиба, кручения и устойчивости.
Алгоритм расчёта ГХС сложного (составного) вида предусматривает использование двух подходов: традиционного [1, 2, 4-8] (путём разбиения сложного сечения на ряд простых и последующего определения всех необходимых параметров простых фигур), и нетрадиционного, основывающегося на использовании компьютерной техники [3] (задание координат точек контура всего сечения во вспомогательной системе координат с последующим обходом контура). Каждый из этих способов расчёта имеет свои достоинства и недостатки и выбор того или иного из них (или их комбинации) остаётся за расчетчиком.
Рассмотрим вначале методику определения ГХС по первому способу.
Пусть задано
произвольное сечение бруса F,связанное с начальными координатными
осями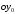 и
и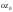 (рис. 5.1). Выделим элемент площади
(рис. 5.1). Выделим элемент площади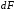 с координатамиy,z.
По аналогии с выражением для момента
силы относительно какой-либо оси можно
составить выражение и для момента
площади, которое называетсястатическим
моментом площади.
с координатамиy,z.
По аналогии с выражением для момента
силы относительно какой-либо оси можно
составить выражение и для момента
площади, которое называетсястатическим
моментом площади.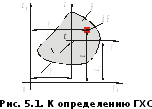
Тогда статические
моменты элемента площади
 относительно осей
относительно осей и
и будут представлены зависимостями:
будут представлены зависимостями:
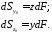
Просуммировав
такие произведения по всей площади
фигуры, получим соответственно статические
моменты относительно осей
 и
и :
:
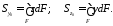 (5.1)
(5.1)
Статические моменты измеряются в мм3, см3, м3.
Осевыми моментами инерцииплощади называются выражения вида:
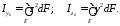 (5.2)
(5.2)
Интеграл вида
 ,
(5.3)
,
(5.3)
называется центробежным моментом инерцииплощади относительно осейyиz. В зависимости от положения осей центробежный момент инерции может быть положительным, отрицательным или равным нулю.
Полярный моментинерции определяется по зависимости
 .
(5.4)
.
(5.4)
Размерность всех величин в формулах (5.2)…(5.4) мм4, см4, м4.
П р и м е р 5.1. Найти статический момент и момент инерции прямоугольного сечения с основаниемbи высотойh(рис. 5.2) относительно собственной центральной осиyи относительно начальной осиy0, проходящей через основание.
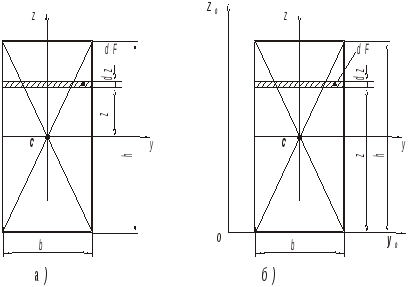
Рис. 5.2. К определению геометрических характеристик прямоугольного сечения
1. Сначала определим
статический момент относительно
собственной центральной оси y(см. формулы 5.1 и рис. 5.2,а), учитывая, что :
:
 ,
,
т.е. статический момент сечения относительно центральной оси равен нулю.
2. Определим статический момент относительно начальной оси y0(рис. 5.2,б):
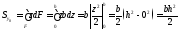
Найдем момент инерции сечения относительно собственной оси y(см. формулы 5.2 и рис. 5.2,а):
 .
.
Найдем момент инерции сечения относительно начальной оси y0(рис. 5.2,б):
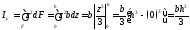 .
.
Пусть
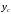 и
и -координаты центра тяжести(ЦТ)
фигурыF. Продолжая
аналогию с моментами сил можно написать
следующие выражения:
-координаты центра тяжести(ЦТ)
фигурыF. Продолжая
аналогию с моментами сил можно написать
следующие выражения:

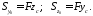 (5.5)
(5.5)
Из формул (5.5) можно найти координаты центра тяжести фигуры
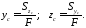 (5.6)
(5.6)
Для многих поперечных сечений простых видов (прямоугольник, треугольник, круг, кольцо, трапеция и т.д.) статические моменты и координаты центров тяжести определены и приведены в справочниках (например, в [2]).
Статический момент площади сложной фигуры, которую можно разбить на простые части (рис. 5.3), определяется как сумма статических моментов каждой части относительно рассматриваемой оси:
 (5.7)
(5.7)
где
 - площадь
- площадь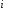 -той
простой фигуры;
-той
простой фигуры;
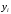 и
и
 - координаты центра тяжести
- координаты центра тяжести -той
простой фигуры.
-той
простой фигуры.

По формулам (5.6) и (5.7) легко найти координаты центра тяжести сложной фигуры:
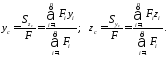 (5.8)
(5.8)
Оси y0z, проведённые через общий центр тяжести фигуры.С(рис. 5.3,б) называютсяцентральными осями. Тогда момент инерции составного сечения относительно центральных осей 0yи 0zможет быть найден как сумма моментов инерции простых фигур относительно этих же осей:
 (5.9)
(5.9)
Центробежный и полярный моменты инерции определим по формулам:
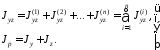 (5.10)
(5.10)
Входящие в (5.9) и (5.10) моменты инерции простых фигур рассчитываются по известным зависимостям:
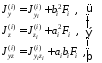 (5.11)
(5.11)
где
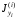 ,
, ,
,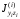 - моменты инерции и центробежный момент
простых фигур относительно собственных
осей,
- моменты инерции и центробежный момент
простых фигур относительно собственных
осей,
 -
расстояние между центрами тяжести
составного сечения и каждой фигуры.
-
расстояние между центрами тяжести
составного сечения и каждой фигуры.
Эти расстояния в центральной системе координат y0zможно выразить так (см. рис. 5.3,б):


 (5.12)
(5.12)
Ранее упоминалось,
что при изменении положения координатных
осей центробежный момент
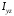 (см. формулу 5.3) может принимать различные
значения, включая ноль. Те оси, относительно
которых центробежный момент инерции
обращается в нуль, называются главными
осями инерции. Поворачивая центральные
осиy0z(рис. 5.3,б) на некоторый угол
(см. формулу 5.3) может принимать различные
значения, включая ноль. Те оси, относительно
которых центробежный момент инерции
обращается в нуль, называются главными
осями инерции. Поворачивая центральные
осиy0z(рис. 5.3,б) на некоторый угол можно
получить экстремальные значения моментов
инерции. Такие оси называютсяглавными
центральными осямии обозначаются
буквамиU иV.
можно
получить экстремальные значения моментов
инерции. Такие оси называютсяглавными
центральными осямии обозначаются
буквамиU иV.
Угол
 можно найти по зависимости:
можно найти по зависимости:
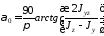 ,
град. (5.13)
,
град. (5.13)
Полученные из
формулы (5.13) два значения угла
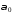 отличаются друг от друга на 90о.
Меньший из этих углов по абсолютной
величине не превышает
отличаются друг от друга на 90о.
Меньший из этих углов по абсолютной
величине не превышает .
Положительный угол
.
Положительный угол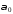 откладывается от горизонтальной осиyпротив часовой стрелки. Проведенную
под углом
откладывается от горизонтальной осиyпротив часовой стрелки. Проведенную
под углом (положительным или отрицательным)
главную ось обозначают буквойU(см. рис 5.4).
(положительным или отрицательным)
главную ось обозначают буквойU(см. рис 5.4).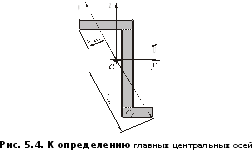
На рис 5.5 приведены некоторые примеры обозначения главных центральных осей в соответствии с указанным правилом. Начальные оси обозначены буквами yиz.
Значения главных моментов инерции можно определить по формулам:
 (5.14)
(5.14)
Напомним, что
главные моменты инерции обладают
свойством экстремальности.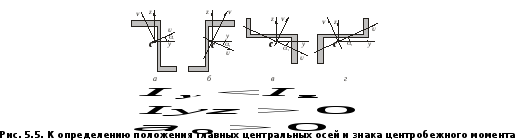
Для выполнения прочностных расчётов различных элементов необходимо определять осевые и полярный момент сопротивления:
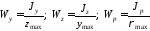 ,
(5.15)
,
(5.15)
где
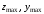 -
координаты наиболее удалённых точек
контура рассчитываемого сечения (см.
рис. 5.3,б);
-
координаты наиболее удалённых точек
контура рассчитываемого сечения (см.
рис. 5.3,б);
 -
наибольший радиус-вектор точки контура
составного сечения.
-
наибольший радиус-вектор точки контура
составного сечения.
В некоторых случаях определение вышеупомянутых параметров ГХС требует достаточно громоздких вычислений. Так, например, сложное сечение с внутренней полостью, изображённое на рис. 5.6 пришлось бы разбивать на большое число простых фигур с последующим определением всех промежуточных величин (площадей, моментов инерции простых фигур и т.д.).
Для таких видов
сечений удобнее использовать второй
метод - метод обхода контура по точкам
с заданными координатами во вспомогательной
системе координат y00z0
[3].
Нумерация точек контура начинается с любой (рис. 5.6) и перемещается вдоль контура по часовой стрелке. При наличии внутренней полости сечения необходимо войти по прямой к точке внутреннего контура и обойти все его пронумерованные точки против часовой стрелки с последующим выходом на наружный контур по той же прямой. Криволинейные очертания контура апроксимируются ломаной линией с необходимой точностью.
Геометрические характеристики сложного сечения, при определении их через координаты точек контура, рассчитываются по зависимостям:
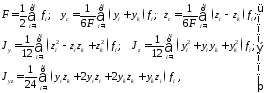 (5.16)
(5.16)
где
 ;
; при
при при
при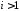 ;
;
N – число точек контура.
Все остальные параметры ГХС определяются по ранее рассмотренным соотношениям. Заметим, что расчеты по второму методу удобнее вести на компьютере.
Правильность расчетов по любому из двух вариантов проверяется такими проверочными условиями:
 (5.17)
(5.17)
П р и м е р 5.2.
Для Z
– образного сечения, показанного на
рис. 5.7, определить положение центра
тяжести yc,
zc
, угол
наклона главных центральных осей инерции
 ,
моменты инерции относительно центральных
осейoy
и oz
и моменты инерции относительно главных
центральных осей U
и V.
,
моменты инерции относительно центральных
осейoy
и oz
и моменты инерции относительно главных
центральных осей U
и V.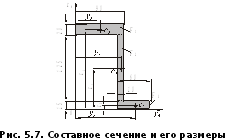
Р е ш е н и е.
Выберем систему начальных осей y0иz0, проведя их так, чтобы они касались крайних точек (слева и снизу) рассматриваемого составного сечения.
Разбиваем фигуру на простые части в виде прямоугольников, находим площади их сечений и общую площадь фигуры:
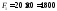 мм2 ,
мм2 ,
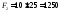 мм2,
мм2,
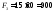 мм2.
мм2.
Общая площадь фигуры
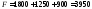 мм2.
мм2.
В выбранной системе осей определяем координаты центров тяжести простых фигур - C1, C2, C3,обозначая их соответственно как y1, z1; y2, z2 и т.д. (рис. 5.7). В таблице 3.1 даются численные значения искомых величин.
Таблица 1 –Промежуточные параметры сечения
|
Фигура |
Площадь фигуры, мм2 |
Координаты ЦТ фигуры в системе y00z0, мм |
Координаты ЦТ фигуры в центральной системе y0z, мм |
Статический момент площади фигуры относительно осей y0 и z0, 104мм3 |
Координаты ЦТ всей фигуры в системе y00z0, мм | |||||||
|
yi |
zi |
ai |
bi |
|
|
yс |
zс | |||||
|
F1 |
1800 |
45 |
150 |
-27,46 |
55,42 |
8,1 |
27 |
|
| |||
|
F2 |
1250 |
85 |
77,5 |
12,54 |
-17,08 |
10,62 |
9,7 | |||||
|
F3 |
900 |
110 |
7,5 |
37,54 |
-87,08 |
9,9 |
0,67 | |||||
|
F |
3950 |
- |
- |
- |
- |
28,62 |
37,37 |
72,47 |
94,58 | |||
Координаты центра тяжести yс,zссоставной фигуры в системеy00z0,определяем по формулам (5.8):
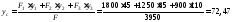 мм.
мм.
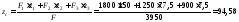 мм,
мм,
Результаты заносим в таблицу
Определим моменты инерции каждого прямоугольника относительно собственных центральных осей (см. пример 5.1):
 мм4,
мм4,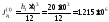 мм4.
мм4.
Значения моментов остальных простых фигур (размерность - мм4) приводим без подробностей расчета:
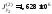 ,
,
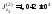 ,
,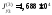 ,
,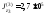 .
.
Моменты инерции каждой простой фигуры относительно центральных осей y и z вычисляются по формулам (5.11). Например:
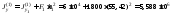 ,
,
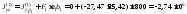 .
.
Остальные значения моментов приводим без подробностей расчета в таблице 5.2.
Таблица 5.2 – Моменты инерции сечения
|
Фигура |
Моменты инерции фигуры, 106мм4, относительно | |||||
|
собственных осей yi, zi |
центральных осей y; z | |||||
|
|
|
|
|
| ||
|
F1 |
0,06 |
1,215 |
5,588 |
2,573 |
-2,74 | |
|
F2 |
1,628 |
0,0104 |
1,993 |
0,207 |
-0,267 | |
|
F3 |
0,0168 |
0,27 |
6,842 |
1,538 |
-2,941 | |
Примечание:
Центробежные моменты инерции фигур
относительно собственных центральных
осей
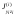 =
0
=
0
Суммируя последние три столбца таблицы 5.2, находим моменты инерции составной фигуры относительно центральных осей y и z :

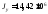 мм4,
мм4,
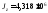 мм4,
мм4,
 мм4.
мм4.
Угол наклона главных центральных осей (рис. 5.8,б) к оси oyнайдем по формуле (5.13):
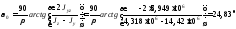 .
.
Главные центральные моменты инерции определяем по формулам (5.14):
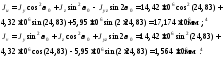
Правильность расчетов проверяем по условию (5.17):
 ,
,
что указывает на достаточную точность полученных результатов.
Реальные конструктивные элементы корпусов и механизмов морских судов (стрингера, шпангоуты, флоры и т.д.) могут включать в себя как стандартные профили (уголки, швеллера, двутавры, полособулбы), так и нестандартные виды сечений простого или сложного очертания. Приводим пример, в котором рассматривается составное сечение, включающее профильный элемент в виде неравнополочного уголка.
П р и м е р 5.3.
Найти положение
главных центральных осей и значения
главных центральных моментов инерции
для сечения состоящего из неравнополочного
уголка сечением 110 70
70 8
мм (ГОСТ 8510-86) и прямоугольной полосы
сечением 20
8
мм (ГОСТ 8510-86) и прямоугольной полосы
сечением 20 160
мм (рис. 5.9).
160
мм (рис. 5.9).
Р е ш е н и е
Прежде всего, определим все необходимые параметры сечения стандартного уголка. По сортаменту прокатной угловой стали, устанавливаем координаты ЦТ уголка (рис. 5.9,а) и значение необходимых ГХС:

В выбранной системе осей составного сечения (рис. 5.9,б) определяем координаты центров тяжести простых фигур - C1, C2,,обозначая их соответственно как y1, z1; y2, z2. В таблице 5.3 даются численные значения искомых величин.
Координаты центра тяжести yс,zссоставной фигуры в системеy00z0,определяем по формулам (5.8):
 cм,
cм,
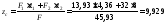 cм.
cм.
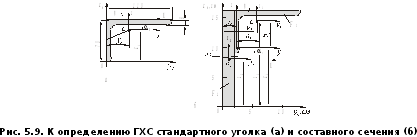
Таблица 5.3 –Промежуточные параметры сечения (рис. 5.9,б)
|
Фигура |
Площадь фигуры, мм2 |
Координаты ЦТ фигуры в системе y00z0, мм |
Координаты ЦТ фигуры в центральной системе y0z, мм |
Статический момент площади фигуры относительно осей y0 и z0, 104мм3 |
Координаты ЦТ всей фигуры в системе y00z0, мм | ||||||
|
yi |
zi |
ai |
bi |
|
|
yс |
zс | ||||
|
F1 |
13,93 |
5,61 |
14,36 |
3,212 |
4,431 |
0,781 |
2,0 |
|
| ||
|
F2 |
32 |
1 |
8 |
-1,398 |
-1,929 |
0,32 |
2,56 | ||||
|
F |
45,93 |
- |
- |
- |
|
- |
- |
2,398 |
9,929 | ||
Поскольку моменты инерции уголка уже известны, то определим их только для полосы относительно собственных центральных осей:
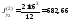 см4,
см4,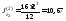 см4.
см4.
Моменты инерции (см4) каждой фигуры относительно центральных осейyиzвычисляются по формулам (5.11):
 ,
,
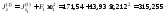 ,
,
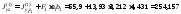 .
.
Остальные значения моментов (см4) приводим без подробностей расчета:
 ,
,
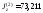 ,
,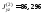
Суммируя составляющие (см. формулы 5.9 и 5.10), находим моменты инерции составной фигуры относительно центральных осей y и z :

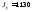 см4,
см4,
 см4,
см4,
 см4.
см4.
Угол наклона главных центральных осей (рис. 5.9,б) к оси oyнайдем по формуле (5.13):
 .
.
Главные центральные моменты инерции определяем по формулам (5.14):

П р и м е р 5.4
Определить
геометрические характеристики поперечного
сечения лопасти руля судна, ( рис. 5.10)
ось которой наклонена под углом 15
градусов к оси движения судна. Профиль
лопасти (в наклоненном положении) задан
координатами 26 точек в таблице 5.4 .
Размеры заданы в см.
Р е ш е н и е
Поскольку сечение рулевой лопасти имеет сложное очертание и его нельзя расчленить на простые фигуры, воспользуемся вторым способом определения ГХС – способом обхода контура, используя формулы (5.16).
Таблица 5.4 – Координаты точек контура лопасти руля (см)
|
№ т. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
y |
0,0 |
1,97 |
6,4 |
10,65 |
14,24 |
26,67 |
38,81 |
50,78 |
62,64 |
|
z |
32,35 |
35,29 |
36,95 |
37,33 |
37,21 |
35,32 |
32,3 |
28,7 |
24,65 |
|
№ т. |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
y |
74,43 |
86,14 |
97,8 |
109,37 |
120,74 |
107,96 |
95,39 |
82,89 |
70,45 |
|
z |
20,36 |
15,77 |
10,94 |
5,87 |
0,0 |
0,59 |
1,99 |
3,64 |
5,52 |
|
№ т. |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
- |
|
y |
58,09 |
45,8 |
33,63 |
21,62 |
9,9 |
6,73 |
3,25 |
0,24 |
- |
|
z |
7,69 |
10,11 |
12,98 |
16,44 |
21,02 |
22,71 |
25,16 |
28,82 |
- |
По заданным
координатам точек контура (на рис. 5.10
точки обозначены цифрами 1…26, обход
сделан по часовой стрелке) определяем,
вначале, значения промежуточной величины
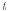 для каждой пары координат рассматриваемой
точки, например, для точки 5 (
для каждой пары координат рассматриваемой
точки, например, для точки 5 (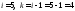 ):
):
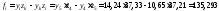 .
.
Всего будет
двадцать шесть значений
 .
.
Далее определяем:
площадь сечения лопасти F, координаты
центра тяжести (в координатной системеy00z0)
сечения ,
моменты инерции
,
моменты инерции и центробежный момент
и центробежный момент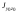 .
.
Выполненные расчеты дают следующие величины:
 см2,
см2,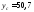 см,
см,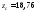 см,
см, см4,
см4,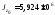 см4,
см4,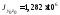 см4.
см4.
Моменты инерции
относительно центральных осей
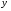 и
и ,
а также главные центральные осевые
моменты инерции и их положение (угол
,
а также главные центральные осевые
моменты инерции и их положение (угол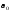 )
определяются по ранее рассмотренным
соотношениям:
)
определяются по ранее рассмотренным
соотношениям:
 и т.д.
и т.д.
Выполненные расчеты дают следующие величины:
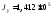 см4,
см4,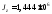 см4,
см4,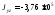 см4,
см4,
 ,
,
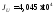 см4,
см4,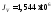 см4,
см4,
В заключение отметим, что расчеты по второму методу целесообразно выполнять на компьютере по составленной программе или используя известный математический редактор MathСad.