
10 (математика)
.doc
Задача 1. Вычислить двойной интеграл
по указанной области
![]()
![]() ,
,
![]()
Решение
О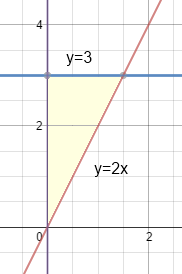 бласть
бласть
![]() является стандартной относительно оси
является стандартной относительно оси
![]() .
.
Сводим двойной интеграл к повторному
по формуле
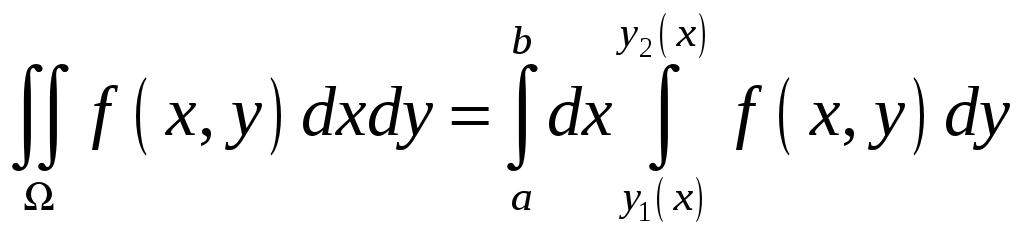 :
:

Поменяем пределы интегрирования:
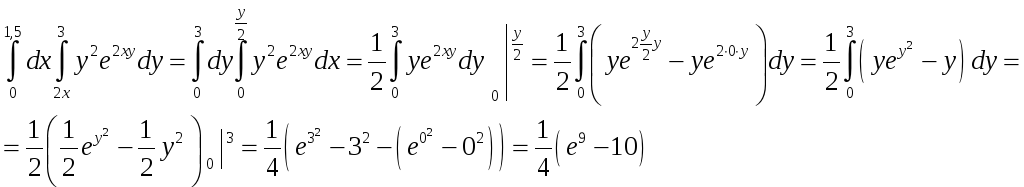
Ответ:
![]()
Задача 2. Вычислить объем указанной
области
![]() с помощью двойного интеграла, переходя
к полярным координатам.
с помощью двойного интеграла, переходя
к полярным координатам.
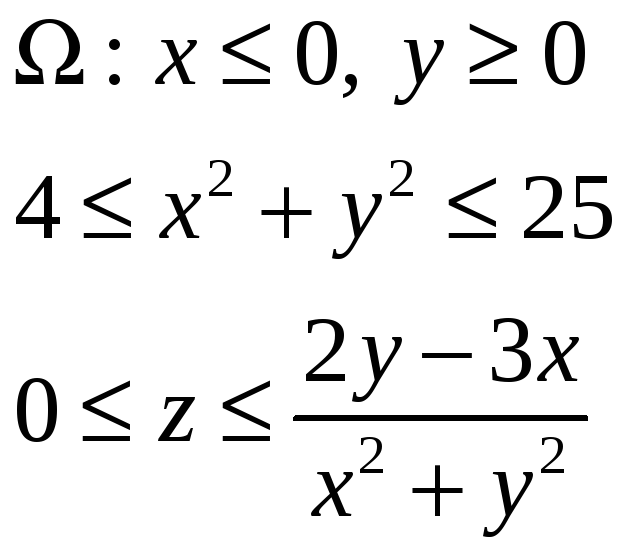
Решение
Введем полярные координаты
![]() .
Требуется вычислить двойной интеграл
по проекции
.
Требуется вычислить двойной интеграл
по проекции
![]() на плоскость
на плоскость
![]() ,
переходя к полярным координатам.
,
переходя к полярным координатам.
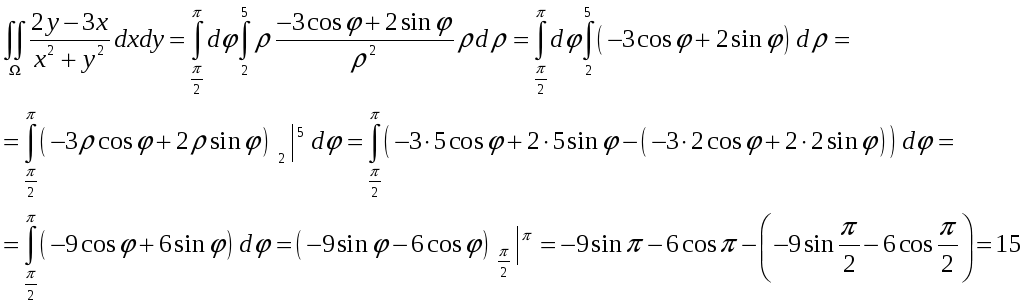
Ответ: 15
Задача 3. Вычислить массу тела
![]() с заданной плотностью
с заданной плотностью
![]() с помощью тройного интеграла
с помощью тройного интеграла
![]()
Решение
Согласно физическому смыслу тройного
интеграла масса тела
![]() равна
равна
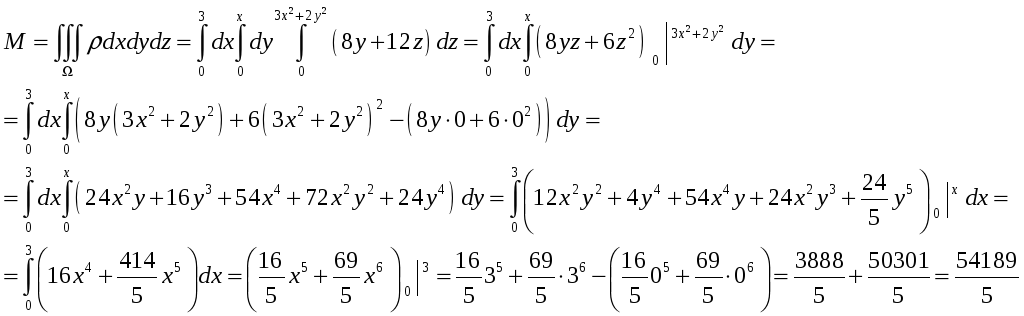
Ответ:
![]()
Задача 4. Вычислить криволинейный
интеграл для заданного векторного поля
![]() вдоль замкнутой ломанной с вершинами
вдоль замкнутой ломанной с вершинами
![]() .
Вычислить этот же интеграл с помощью
формулы Грина.
.
Вычислить этот же интеграл с помощью
формулы Грина.
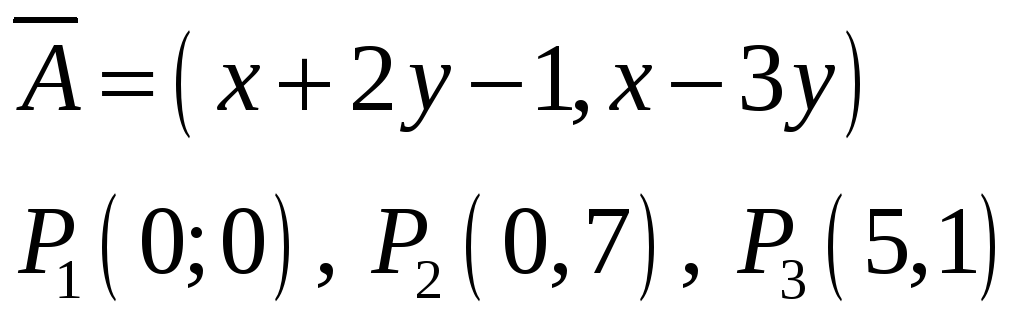
Решение
Пусть векторное поле
![]() задано в виде
задано в виде
![]()
Замкнутая ломаная задана своими вершинами
![]() .
.
Формула Грина
![]()
Последний интеграл по геометрическому
смыслу двойного интеграла численно
равен площади треугольника с вершинами
![]() :
:
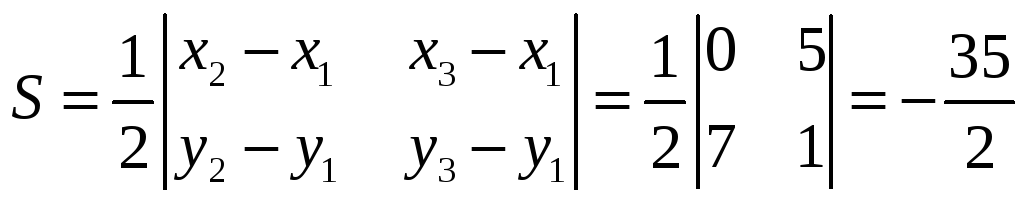
Таким образом,
![]()
Для вычисления криволинейного интеграла
произведем параметризацию отрезков
![]() :
:
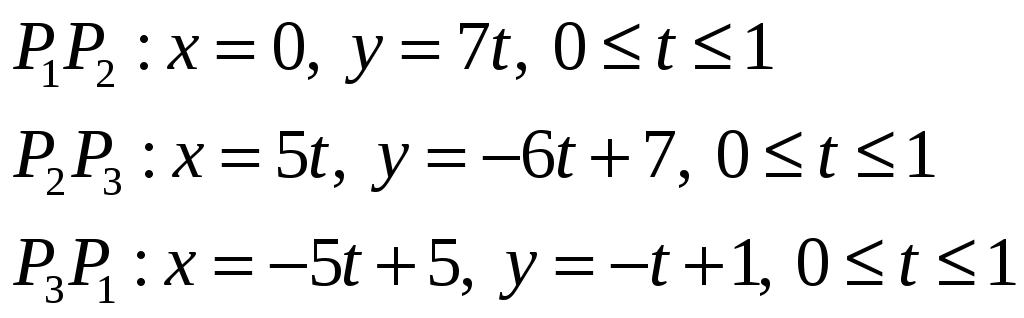
Далее, используя аддитивность криволинейного интеграла, получаем:
![]()
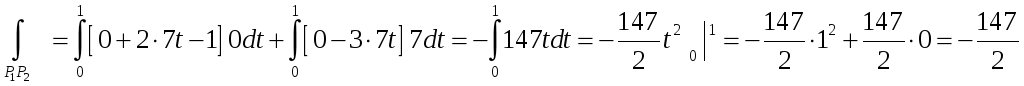
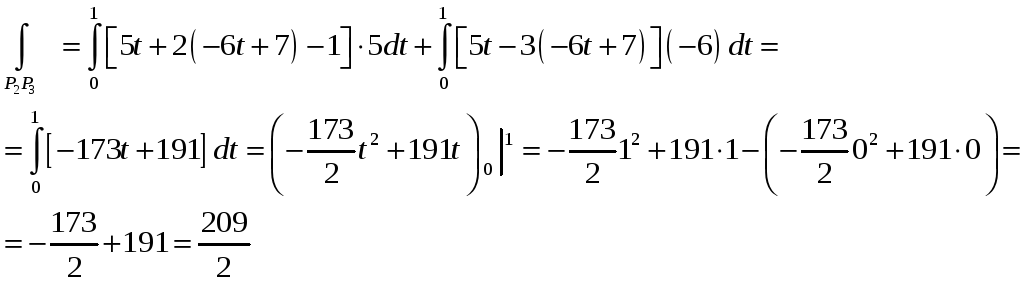
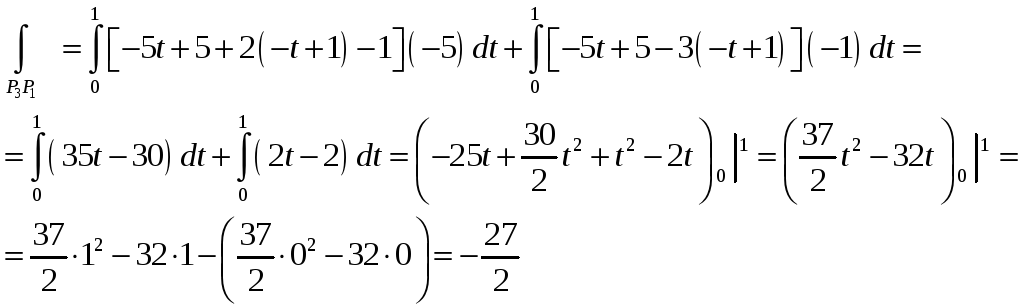
Складывая полученные значения, находим:
![]()
Ответ:
![]()
Задача 5. Вычислить криволинейные
интеграл по кривой
![]() от точки
от точки
![]() до
до
![]() от заданного векторного поля
от заданного векторного поля
![]() .
.
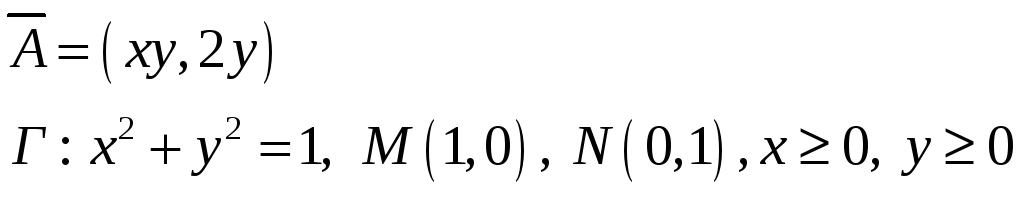
Решение
В данном случае удобнее представить
![]() в параметрической форме:
в параметрической форме:

В таком случае криволинейный интеграл
по
![]() выведется к определенному интегралу:
выведется к определенному интегралу:
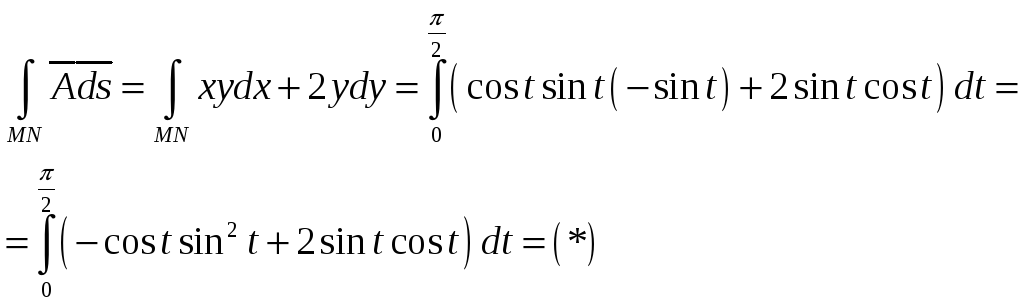
![]()
![]()
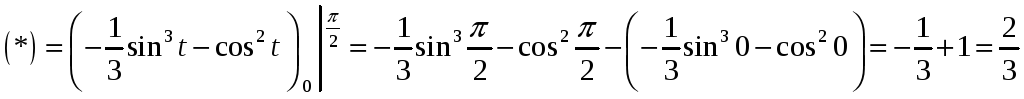
Ответ:
![]()
Задача 6. Вычислить все значения
величины
![]()
![]()
Решение
Прежде всего, вычислим
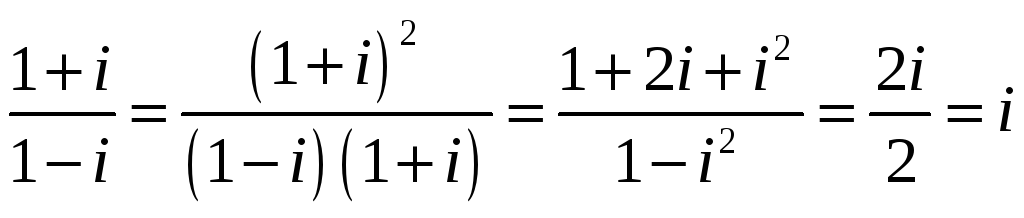
Вычислим
![]() .
.
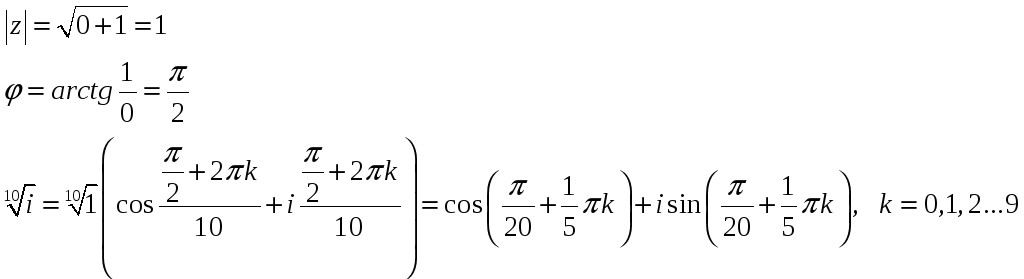
При
![]()
При
![]()
При
![]()
При
![]()
При
![]()
При
![]()
При
![]()
При
![]()
При
![]()
При
![]()
Задача 7. Найти модуль и аргумент производной от заданной функции
![]()
Решение
Производную от этой функции вычисляем по обычным правилам:
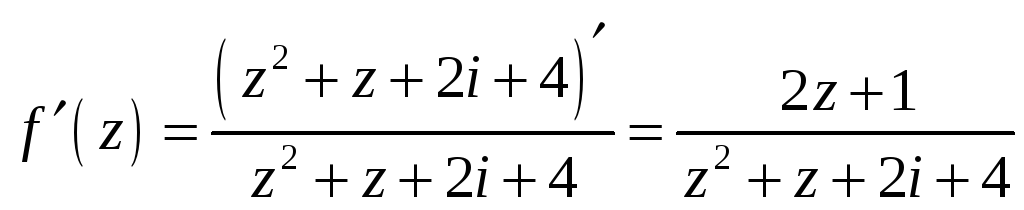
Разложим на линейные множители знаменатель этой дроби. Для этого найдем корни уравнения.
![]()
![]()
Найдем модуль
![]() :
:
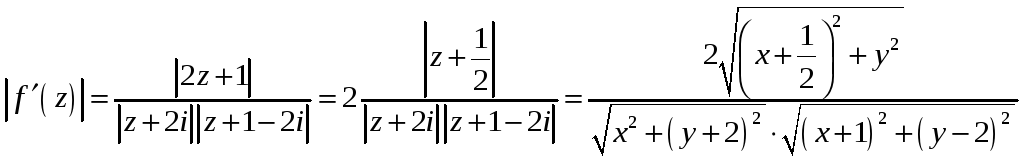
Для определения
![]() найдем аргументы каждого линейного
множителя в
найдем аргументы каждого линейного
множителя в
![]() :
:
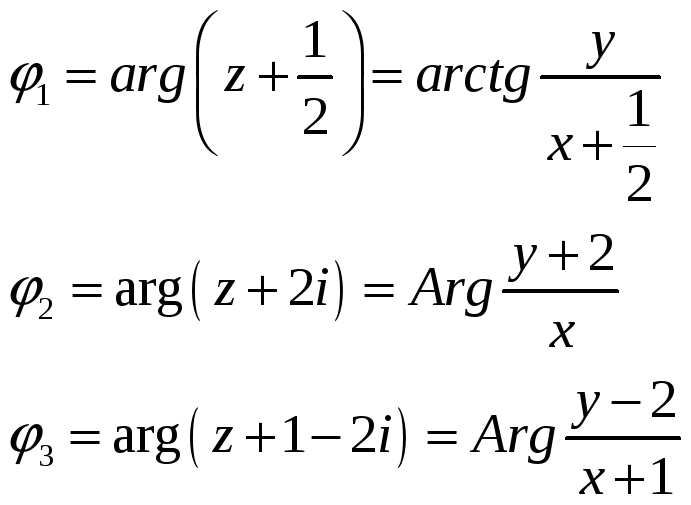
Следовательно, аргумент производной
![]() равен:
равен:
![]()
Задача 9. Найти общее решение дифференциального уравнения с разделяющимися переменными.
![]()
Решение
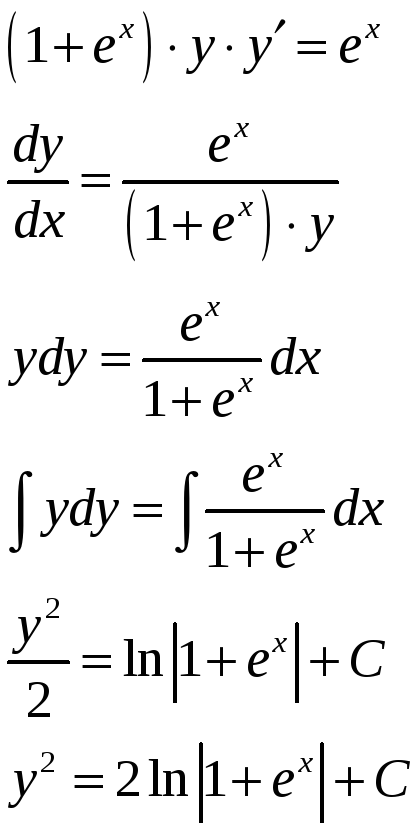
Задача 10. Найти общий интеграл однородного дифференциального уравнения
![]()
Решение
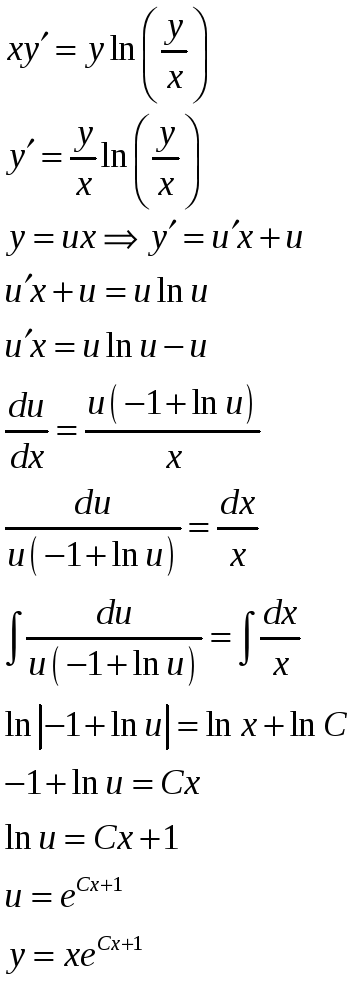
Задача 11. Решить задачу Коши для линейного уравнения первого порядка
![]()
Решение
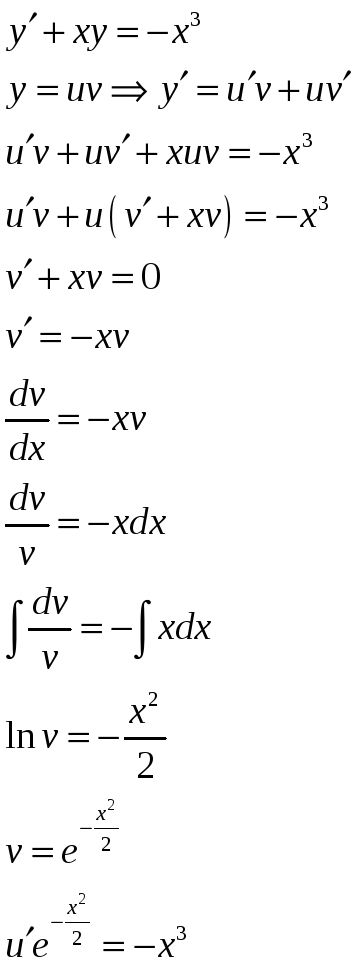
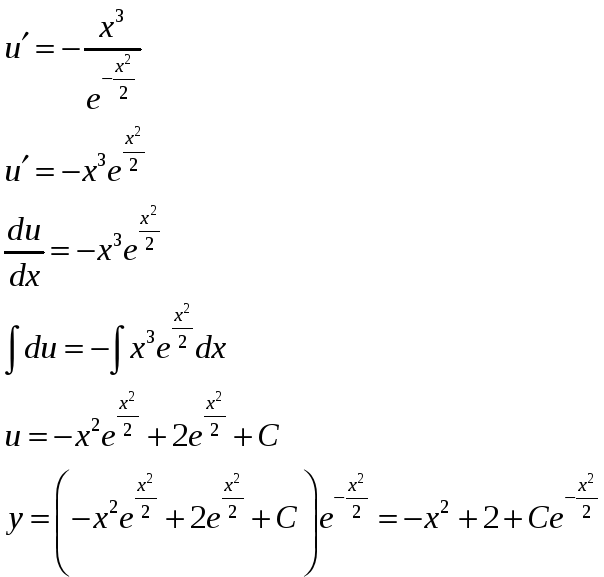
Найдем решение задачи Коши:

Решение задачи Коши найдено:
![]()
Задача 12. Проинтегрировать уравнение в полных дифференциалах
![]()
Решение
В этом уравнении
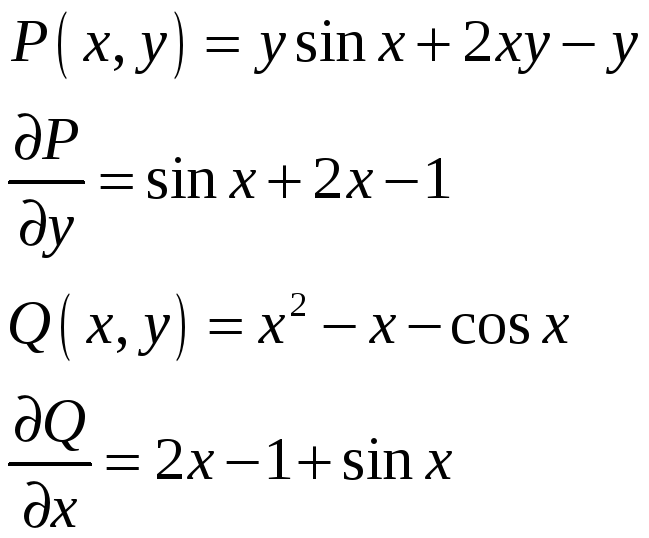
Поскольку
![]() ,
левая часть данного уравнения есть
полный дифференциал некоторой функции
,
левая часть данного уравнения есть
полный дифференциал некоторой функции
![]() .
.
![]()
Определим это функцию. Из равенства
![]() следует, что
следует, что
![]()
Чтобы определить неизвестную функцию
![]() ,
воспользуемся другим равенством
,
воспользуемся другим равенством
![]() и получаем
и получаем
![]()
Отсюда
![]()
Таким образом, получаем общее решение
исходного уравнения в виде
![]() ,
то есть
,
то есть
![]()
Задача 14. Найти общее решение линейного уравнения с постоянными коэффициентами
![]()
Решение
Характеристическое уравнение:
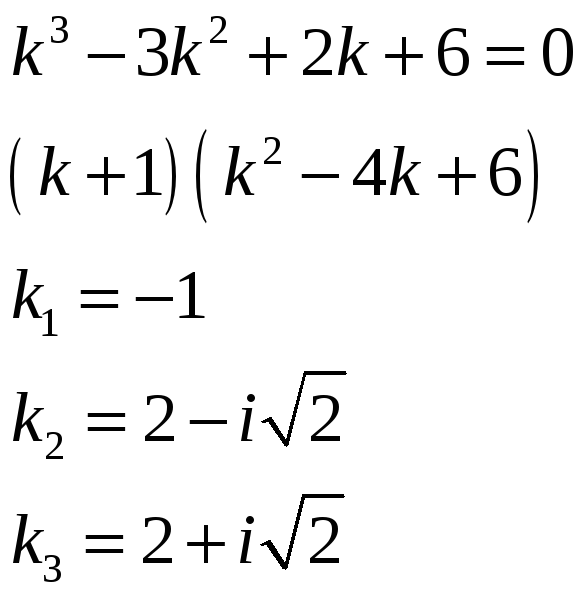
В соответствии с этим получаем общее решение заданного уравнения:
![]()
Задача 15. Решить задачу Коши для линейного уравнения второго порядка

Решение
Характеристическое уравнение имеет вид:
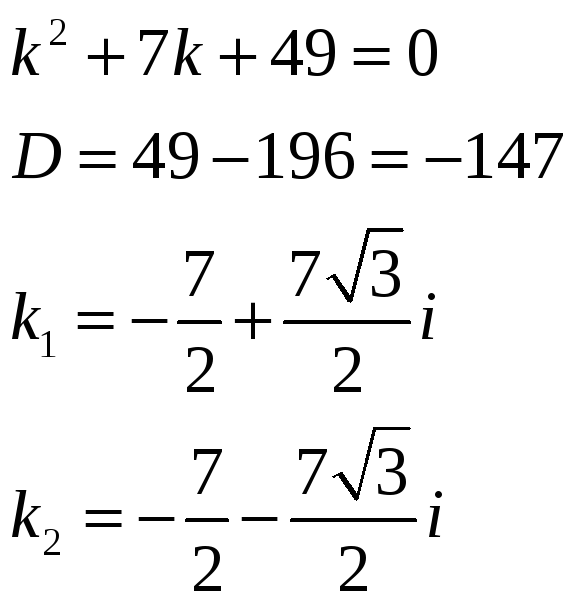
В этом случае общее решение однородного уравнения представляется в виде:
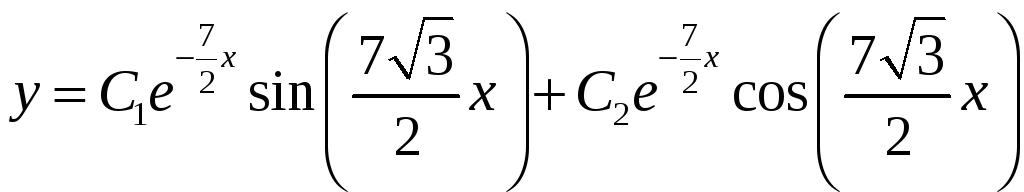
Найдем частное решение неоднородного уравнения.
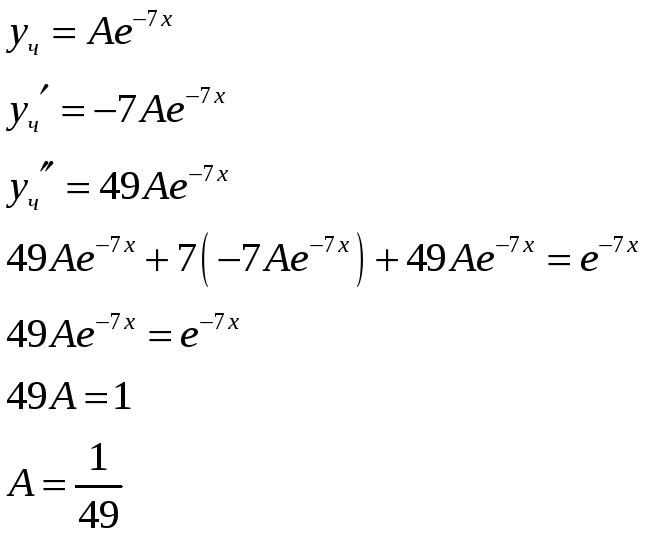
![]()
Тогда общее решение неоднородного дифференциального уравнения имеет вид:
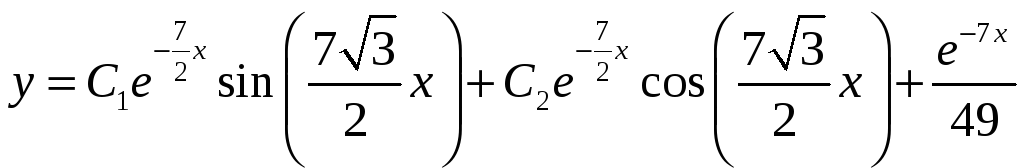
Найдем частное решение, удовлетворяющее начальным условиям.
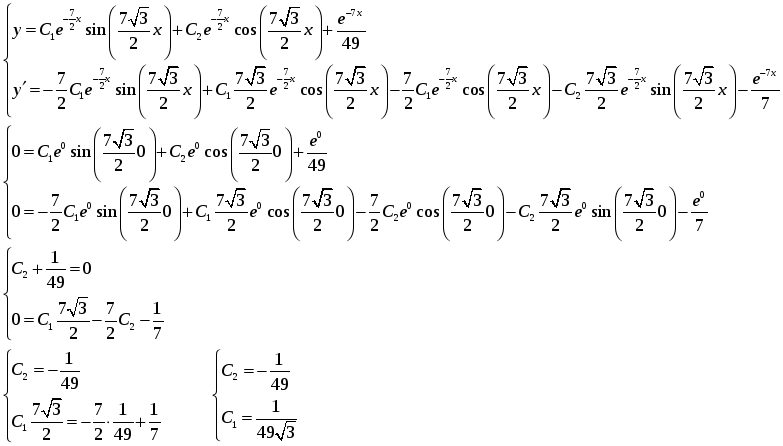
Итак, частное решение

Задача 18. Исследовать на устойчивость систему ОДУ
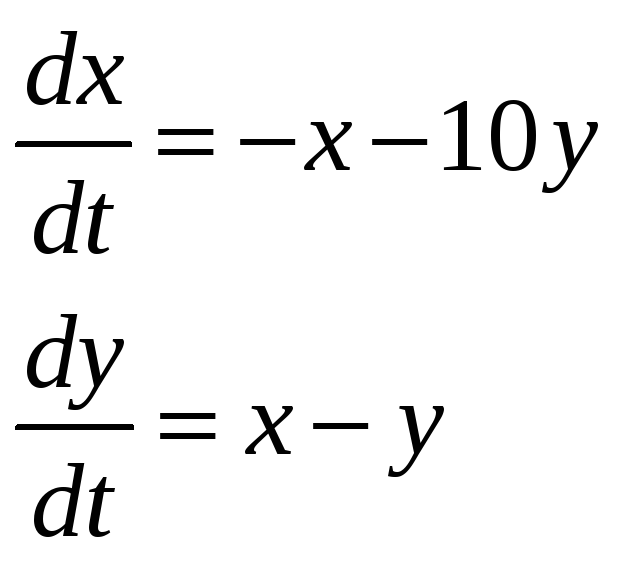
Решение
Найдем корни характеристического уравнения:
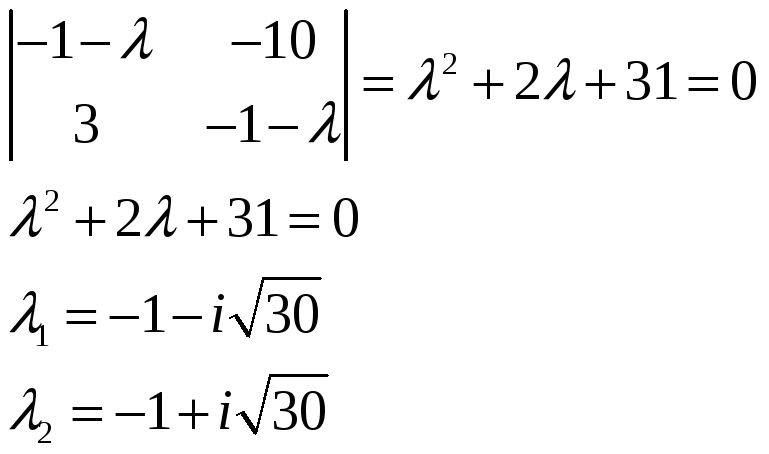
Корни комплексно-сопряженные, причем
![]() .
Устойчивый фокус.
.
Устойчивый фокус.
